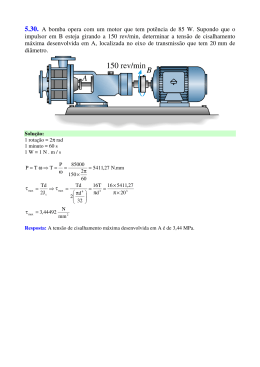
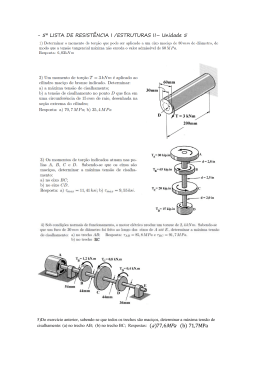
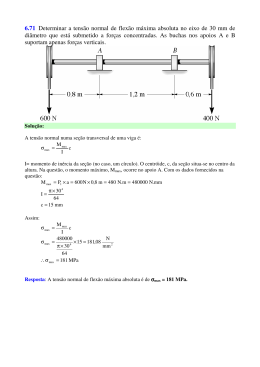
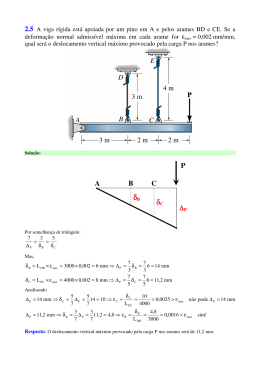
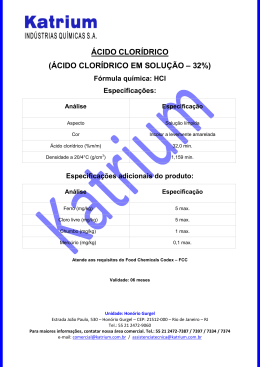
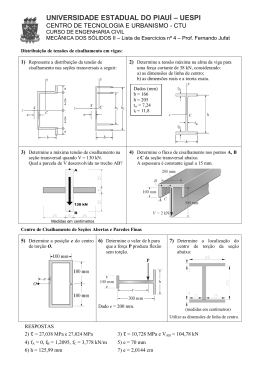
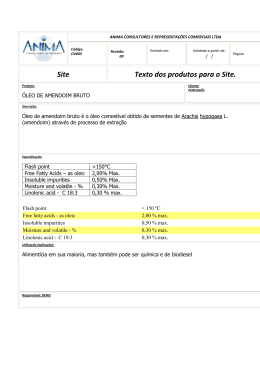
7.15 Determinar a tensão de cisalhamento máxima no eixo com seção transversal
circular de raio r e sujeito à força cortante V. Expressar a resposta em termos da área
A da seção transversal.
Solução:
A tensão de cisalhamento máxima é:
VQ
τ max =
Ix b
onde:
 πr 2   4r  2r 3
 ×   =
Q = 
2
3

  3π 
πr 4
4
b = 2r
Ix =
Assim:
τ max =
VQ
Ix b
2r 3
4V
4V
= 43 =
=
2
3A
3πr
πr
2r
4
V
⇒ τ max
Resposta: A tensão de cisalhamento máxima no eixo com seção transversal circular de raio r e
4V
sujeito à força cortante V é de τ max =
.
3A