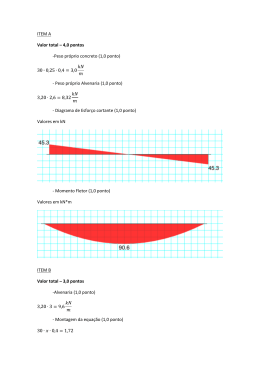
RESISTÊNCIA DOS
MATERIAIS
UNICAMP
MÓDULO 2 – ESFORÇOS
SOLICITANTES
PROF. EDUARDO COELHO
Os desafios que parecem impossíveis
tornam-se fáceis mediante a capacitação
ESFORÇOS SOLICITANTES
p
p
H
H
M
N
z
Apoio
móvel A
x
y
N
V
M
V
Apoio
fixo B
R
vA
R
v
h
São esforços internos que equilibram
cargas e reações situadas à esquerda
ou à direita de uma determinada seção
transversal genérica
R
R
vB
R
R
h
vB
X
p
M, N e V equilibram as cargas e
reações situadas à esquerda da
seção genérica I - I
M
I
N
H
I
V
p.x
x/2
x
F
F
x
= 0 N = H
y
= 0  V = R v - p.x
 Mi = 0  Mi = R v .x - p.x.
x
2
CONVENÇÃO DE SINAIS
R
vA
N > 0 SE FOR DE TRAÇÃO (ALONGA AS FIBRAS) – FORÇA NORMAL
y
V > 0 SE A RESULTANTE À ESQUERDA E O ESFORÇO CORTANTE
PROVOCAREM BINÁRIO QUE GIRE NO SENTIDO HORÁRIO –
FORÇA CORTANTE
M > 0 SE PROVOCAR TRAÇÃO NAS FIBRAS INFERIORES –
MOMENTO FLETOR
TRAÇADO DE DIAGRAMAS DE M, N E V
OBJETIVO : ENCONTRAR NA ESTRUTURA TODA, A VARIAÇÃO DOS ESFORÇOS
SOLICITANTES E SUA DISTRIBUIÇÃO, DE MODO A SELECIONAR OS ESFORÇOS
CRÍTICOS, A SEREM USADOS NO DIMENSIONAMENTO DAS BARRAS
OBS : A BARRA, DIMENSIONADA PARA RESISTIR A ESSES ESFORÇOS
CRÍTICOS, FICA SUJEITA A TENSÕES LIMITES NESSAS SEÇÕES TRANSVERSAIS
– NAS DEMAIS AS TENSÕES SE SITUAM ABAIXO DESSES PATAMARES
N = Força normal crítica
max
V = Força cortante crítica
max
M = Momento fletor crítico
max
Exemplo de vigas sobre 2 apoios (cargas concentradas)
y
REAÇÕES DE APOIO
II
I
A
H
3,0 tf
2,0 tf
III
 F = 0  V + V = 5tf
 M = 0  2,0.2,0 + 3,0.4,5 - V .7,5 = 0
B
I
A
y
x
II
III
A
A
 VA = 2,67tf
V
A
F
B
x
2,67
+
B
 VB = 2,33tf
V
2,0 m
B
2,5 m
= 0  HA = 0
3,0 m
2,0
V (tf)
0,67
-
DIAGRAMAS de M e V
2,67
M = 2,67.x (linear)
M
2,33
2,67
2,0
M
x
5,33
x,
2,33
2,33
7,0
M (tf.m)
2,67
0,67
(constante)
M= 2,67.x – 2,0.(x – 2,0)
M = 2,33.x,
Viga sobre 2 apoios
x
(carga distribuída)
p
Por simetria, V = V = p.l / 2
A
VA
V
l/2
p.l
2
B
B
l/2
p.l
p.l
- p.x,(x = o)  V =
2
2
p.l
x
l
x2
p.l2
l
M = .x - p.x. = p. .x - p.  Mmax. = ,(x = )
2
2
2
2
8
2
V=
+
V (força cortante)
-
p.l
2
M (momento fletor)
M desenhado do lado em que
as fibras
são tracionadas
p.l²/8 = M
max.
Na seção onde M é máximo, a força cortante é nula
 dM 
 dx  = V


dM p.l
=
- p.x = V
dx
2
l
p.l 2
Quandox = ⇒ M = Mmax. =
2
8
x
p
M
p.x
p.l/2
V
p.l
p.x 2
M = .x 2
2
x/2
M TRACIONA (ALARGA) AS FIBRAS INFERIORES
VIGA EM BALANÇO
M
x
p
A
Equilíbrio
F
F
A
H
x
=0⇒H=0
y
= 0 ⇒ VA = p.l
 MA = 0 ⇒ MA = p.l.
V
A
l
l
l2
= p.
2
2
V
p
DIAGRAMAS
N=0
p.l
+
V
M
x
X=l/2
V = p.x
pl²/8
p.l²/2
M
(linear)
x
x2
Mi = p.x. = p.
2
2
(Parábola 2.º grau)
SUPERPOSIÇÃO DE EFEITOS
x
P
p
M
H
l
V
P
V
x
P+p.l
P
+
N=o
M
x=l/2
p
x
x
pl²/8
M
M= P.l+p.l²/2
Vx = P + p.x
x2
Mx = P.x + p.
2
EXEMPLO
y
10
= 5p
2
 MA = 0 ⇒ VA .6 - p.10.3 = 0 ⇒ VA = 5p
 Fy = 0 ⇒ VA = VB = p.
p= 1 tf/m
x
V = 5 tf
A
2m
V
(tf)
-
B
6m
3
+
M=1.x.x/2= x²/2
V
2m
V=0
2
V = 1.x
2
-
M
N=0
x
+
V
Mx = 5( x - 2)- 1.x.
3
x = 5m ⇒ M = Mmax
V=0
2,0
2,0
1 tf/m
x
2
= 2,5tf.m
1 tf/m
M
M
(tf.m)
2,5
1.6²/8=4,5 tf.m
max
5,0 tf
X=5m
2,0 m
GENERICAMENTE, se M > M
A
M
A
M
p
V
A
B
V
B
l
a
B
, resulta:
l M -M
VA = p.  A B
2
l
l M -M
VB = p. - A B
2
l
Diagramas de M e V
b
V
A
p
V
B
M
l
p.
2
p.
M
A
l
2
M
A
M
B
p.l²/8
MA - MB
l
B
MA - MB
A curvatura da parábola segue o sentido da carga p
l
TRELIÇAS PLANAS (Cargas aplicadas nos nós)
y
2,0 tf
2,0 tf
1,0 tf
I
3
1
H
I
0
5
5-5
7
9 4-4 11
1,0 tf
13
15
θ
0
17
1,2 tf
(1,5 m)
θ
2
4
6 3 - 38
2-2
10
12
5-5
V
0
14
16
x
V
16
(8 X 2,0 m)
 F = 0 ⇒ H = 1,2 tf
 F = 0 ⇒ V + V = 7. 2,0 + 2 .1,0 = 16,0 tf
 M = 0 ⇒ 2,0 ( 2,0 + 4,0 + 6,0 + 8,0 + 10,0 + 12,0 + 14,0 ) + 1,0 ( 16,0 ) - V
x
0
Y
0
0
V0 = 7,89 tf
V16 = 8,11 tf
16
16
.16,0 - 1,2.1,5 = 0
Utilizando as equações de equilíbrio no plano, obtêm-se os
esforços solicitantes nas barras, que são sempre axiais
N > 0 – tração N < 0 - compressão
Corte I - I
Corte 2 - 2
1,0 tf
1,0 tf
N
13
N
03
x
= 0 ⇒ N13 = 0
y
= 0 ⇒ N01 = 1,0 tf
N
02
0
01
F
F
θ
1,2 tf
N
7,89 tf
F
F
Y
= 0  7,89 - 1,0 + N03 .sen θ = 0  N03 = - 11,48 tf
x
= 0  1,2 + N02 - 11,48 . cos θ = 0 N02 = 7,98 tf
sen θ = 0,6
cos θ = 0,8
Corte 4 – 4
Corte 3 - 3
2,0 tf
N
6-7
N
N
7-9
9-11
9
N 4-6
N
6
6-8
N
 Fx = 0 N46 = N68
F
y
= 0  N67 = 0
8-9
(Não há forças
aplicadas em 6)
Da mesma forma, resulta que:
N2-3 = N10-11 = N14-15  0
N4-5 = N12-13 = - 2,0 tf
N7-9 = N9-11
N8-9 = - 2,0 tf
CORTE de RITTER (Corte 5 – 5)
2,0 tf
Passando um corte por 3 barras,
N11-13
duas a duas concorrentes em
13
um ponto, fazemos somatória
N
11-12
de momentos em relação a
esse ponto, encontrando o
N10-12 12
esforço na 3.ª barra
N15-17 = -1,2 tf
2,0 tf
N16-17 = -1,0 tf
1,0 tf
15
17
1,2 tf
14
1,5 m
16
8,11 tf
2,0 m 2,0 m 2,0 m
M
12
= 0 - N11-13 . 1,5 - 1,2.1,5 +2,0.2,0 +1,0.4,0 - 8,11.4,0 = 0N11-13 = - 17,5 tf
N10-12 .1,5 +2,0.2,0 +2,0.4,0 +1,0.6,0 - 8,11.6,0 = 0N10-12 = 20,44 tf
F
y
= 0N11-12 .0,6 + 8,11- 2,0 - 2,0 - 1,0 = 0 N11-12 = - 5,18 tf
2,0 tf
2,0 tf
1,0 tf
Fazendo o corte 5-5 resulta:
N
3
1
5
57
7
N
47
1,2 tf
0
2
4
N
1,5 m
6
46
7,89 tf
2,0 m
2,0 m 2,0 m
F = 0  N .0,6 + 7,89 - 1,0 - 2,0 - 2,0 = 0 N = -4,82tf
 M = 0 7,89.6,0 - 1,2.1,5 - 1,0.6,0 - 2,0.4,0 - 2,0.2,0 - N
y
47
7
47
46
.1,5 = 0
 N46 = 18,36tf
M
4
= 0 7,89.4,0 - 1,0.4,0 - 2,0.2,0 + N57 .1,5 = 0 N57 = -15,71tf
Equilíbrio do nó 17, resulta
1,0 tf
N15-17 = -1,2 tf
N16-17 = -1,0 tf
N
15-17
17
N
15-16
16
Equilíbrio do nó 10 resulta:
N8-10 = N10-12 = 20,44 tf
Equilíbrio do nó 16
leva a :
8,11- 1,0 + N15-16 .0,6 = 0
N15-16 = - 11,85 tf
N14-16 = - N15-16 .0,8 = 9,48 tf
N
14-16
8,11 tf
1.2 tf
Feitos os equilíbrios e cortes restantes
nos nós e barras, chegamos aos
resultados dos esforços nas barras,
como indicado na figura:
0,0
-15,71
-15,71
-23,12
-2,0
-1,0
7,98
0,0
18,36 tf
18,36
-17,5
-17,5
-2,0
0,0
7,98
-23,12
-2,0
0,0
20,44
20,44
Esforços nas barras em tf
N>0 ............. tração
-1,2
N<0 ............. compressão
-1,0
0,0
9,48
9,48