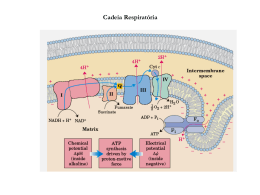
Sistemas de elétrons fortemente correlacionados:
um enfoque computacional
André Luiz Malvezzi
Departamento de Física
Faculdade de Ciências
UNESP - Bauru
Setembro - 2003
La1-x Cax Mn O3
• Estrutura e estequiometria
Composto precursor : La Mn O3
La : [Xe](5d)(6s)2 perde 3 elétrons : 1 x (+3) = +3
O : [He](2s)2(2p)4 ganha 2 elétrons : 3 x (-2) = -6
Mn : [Ar](3d)5(4s)2 perde 3 elétrons : 1 x (+3) = +3
La3+Mn3+ O32Composto dopado : La1-x Cax Mn O3
Ca : [Ar](4s)2
perde 2 elétrons
(La1-x)3+ (Cax)2+ (Mn1-x)3+ (Mnx)4+ (O3)2x:0
1
2
• Diagrama de fase experimental
CAF = antiferromagnética “canted”
CO = carga ordenada
3
FI = ferromagnética isolante
FM = ferromagnética metálica
AF = antiferromagnética
• O Modelo
H = -t

–
( cit cj + h.c. )
JH

i
<ij>
+ J’
S
if
. Sjf
+
U
<ij>

ni ni
i
t=1
JH , J’ , U , V > 0
4


Sif . sic
+ V
 nn
i j
<ij>
• Estudo numérico de sistemas finitos
• Calcular as propriedades físicas macroscópicas
• Estudar sistemas finitos e extrapolar resultados
• Escolher o tamanho do sistema, o número de
elétrons e os parâmetros de interação ( JH , J’, U e V ) :
Construir uma representação
Matricial da Hamiltoniana
Diagonalizar
numericamente
Propriedades
físicas do modelo
• 12 átomos com 10 elétrons : dimensão da matriz e´  1,5 x 109 !!!
• Método de Lanczos
• Algorítmos do grupo de renormalização da matrix densidade (DMRG)
5
• Diagramas de fase teóricos
JH = 40
J’ = U = V = 0
FM = ferro
J’ = 0.05
U = 16
AF = antiferro
PS1,PS2 = separação de fase
CO = carga ordenada
CD = carga desordenada
IC = incomens.
PS = separação de fase
6