MATEMÁTICA
SATVIRTUA
CRITÉRIOS DE DIVISIBILIDADE
PROF PEDRÃO
DIVISOR DE UM NÚMERO
São os números pelos quais podemos efetuar a
divisão com o resto sendo igual a zero.
# Por 2
Um número é divisível por 2 quando o algarismo das
unidades for par (0, 2, 4, 6, 8).
02) Quais o divisores de 18?
R: 1, 2, 3, 6, 9, 18
# Por 3
Um número é divisível por 3 quando a soma dos seus
DECOMPOSIÇÃO EM FATORES PRIMOS
algarismos for divisível por 3.
Um número pode ser decomposto em fatores primos
através de divisões sucessivas.
# Por 4
Um número é divisível por 4 quando o número
03) Faça a decomposição em fatores primos do
formado pelos dois algarismos da direita for divisível
número 420
por 4 ou quando forem ambos iguais a zero.
R: 2 . 3. 5. 7
# Por 5
NÚMEROS PRIMOS ENTRE SI
Um número é divisível por 5 quando o algarismo das
Dois números são primos entre si quando o único
unidades for 0 ou 5.
divisor comum é o 1.
# Por 6
MÍNIMO MÚLTIPLO COMUM
Um número é divisível por 6 se for divisível por 2 e 3
O mmc entre números é o menor valor comum entre
simultaneamente.
os valores do conjunto intersecção dos múltiplos dos
2
números.
# Por 10
Um número é divisível por 10 se o algarismo das
04) Qual o mmc entre 18 e 24?
unidades for zero.
R: 72
NÚMEROS PRIMOS
05) Três amigos encontraram-se num certo dia na
Um número é primo quando admitir como divisores
cidade de Florianópolis - SC e jantaram juntos. O
apenas ele próprio e a unidade.
primeiro deles visita esta cidade a cada 6 dias, o
Ex: 2, 3, 5, 7, 11, 13, 17, 19...
segundo a cada 8 dias e o terceiro a cada 5 dias.
O número 1 não é primo e o 2 é o único número par
Estes três
amigos marcaram
que é primo.
novamente
no
próximo
de
encontro.
jantar
juntos
Este,
deverá
acontecer após:
MÚLTIPLO DE UM NÚMERO
R: 120 dias
É o produto do número por um outro número.
06) A tabela mostra aproximadamente a duração do
Lembra da tabuada?
ano (uma volta completa em torno do Sol) de alguns
01) Quais os 5 primeiros múltiplos de 7?
planetas do sistema solar, em relação ao ano
R: 7, 14, 21, 28, 35
terrestre.
2009
Neste curso os melhores alunos estão sendo preparados pelos melhores Professores
1
MATEMÁTICA
SATVIRTUA
Planeta
Duração do ano
Júpiter 12 anos terrestres
Saturno 30 anos terrestres
Urano
84 anos terrestres
PROF PEDRÃO
10) A proprietária da floricultura “Flores Belas” possui
100 rosas brancas e 60 rosas vermelhas e pretende
fazer o maior número de ramalhetes que contenha,
cada um, o mesmo número de rosas de cada cor.
Se, em uma noite, os planetas Júpiter, Saturno e
Quantas rosas de cada cor devem possuir cada
Urano são observados alinhados, de um determinado
ramalhete?
local na Terra, determine, após essa ocasião, quantos
R: 5 rosas brancas e 3 rosas vermelhas
anos terrestres se passarão para que o próximo
alinhamento desses planetas possa ser observado do
EXPRESSÕES NUMÉRICAS
mesmo local.
A resolução de uma expressão numérica deve
R: 420 anos
obedecer a ordem de operações:
07) Dois veículos partem juntos de um mesmo ponto,
# Quanto aos sinais gráficos
percorrendo caminhos diferentes. O primeiro retorna
1º) Parênteses
ao ponto de partida a cada 40 min e o segundo, a
2º) Colchetes
cada 50 min. Se ambos saíram às 20h, que horas eles
3º) Chaves
estarão novamente juntos?
R: 23h 20min
# Quanto às operações
1º) Potenciação ou radiciação
MÁXIMO DIVISOR COMUM
2º) Multiplicação ou divisão
O mdc entre números é o maior valor comum entre os
3º) Adição ou subtração
valores do conjunto intersecção dos divisores dos
números.
11) Carlos e Jorge são amigos e gostam muito de
matemática. Até para dizer as suas idades eles fazem
08) Qual o mdc entre 20 e 32?
questão de usar cálculos. Quando perguntam a Carlos
R: 4
a sua idade ele responde: "Tenho o dobro de 15, mais
26, dividido por quatro". Para a mesma pergunta, a
09) Um comerciante de materiais para cercas recebeu
resposta de Jorge é: "Tenho o triplo de 2 mais 5,
12 troncos de madeira de seis metros de comprimento
menos 9". As expressões que determinam a idade de
e outros 9 de oito metros. Ele determinou a um de
Jorge e de Carlos e suas idades são:
seus funcionários que trabalha na preparação dos
materiais que cortasse os troncos para fazer estacas,
todas de mesmo comprimento, para utilizá-las numa
cerca para área de pastagem. Disse-lhe ainda que os
comprimentos deviam ser os maiores possíveis. A
tarefa foi executada pelo funcionário, e o número total
de estacas preparadas foi:
R: 72 estacas
R:
2 ⋅ 15 + 26
= 14
4
Jorge → 3 ⋅ (2 + 5) − 9 = 12
Carlos →
12) A estatura de um adulto do sexo feminino pode ser
estimada, através das alturas de seus pais, pela
expressão:
( y − 13 ) + x
. Considere que x é a altura
2
da mãe e y a do pai, em cm. Somando-se ou
subtraindo-se 8,5 cm da altura estimada, obtém-se,
2
2009
Neste curso os melhores alunos estão sendo preparados pelos melhores Professores
MATEMÁTICA
SATVIRTUA
respectivamente, as alturas máxima ou mínima que a
filha adulta pode atingir. Segundo essa fórmula, se
João tem 1,72 m de altura e sua esposa tem 1,64 m,
sua filha medirá, no máximo:
R: 1,70m
está andando, em m/seg, a uma velocidade de:
R: 22m/seg
O
20)
3
uma velocidade de 100 milhas por hora, o que
equivale, em km/h, a uma velocidade igual a:
2
21) O valor da expressão
R:
(a + b )2
2
a +b
2
é igual a:
3
26
3
4⋅
multiplicá-lo por:
23) Qual é o valor da expressão
10 − 3
é igual a:
R: −
R: 300,1
17) O valor da expressão 5
R: −
−1
−
2
R:
1
, é:
2
R:
3
 1
 + 
2
2
−2
⋅
5
, obtém-se:
2
49
4
 1  4
 − 
 2 
O
 1
: 
2
R: 00
valor
3
da
  1 6
−7
 ⋅  −  − 2 , é:
  2 
4 1 0,2
⋅ −
3
2 0,1 , é:
25) O valor de E =
2 1 6 2
: + ⋅
3 3 5 3
expressão
10
21
26)Calcule:
2
2
3  4  5   7   7   3  
1
−  ⋅   −  −  :   ⋅  −  +  − 3 
2  5  3   2   5   2  
2
R:
2009
153
10
20
3
R: −
19)
1
1
+2−
5
4:
1 1
−
3 2
 4
7 − 2 2 ⋅ 1 − 
 3  , é:
24) O valor de m =
1
1+
4
3
10
18) Efetuando-se 
1
e
2
1 1
−  : (0,5 )2 , é:
 2 3
15) Dividir um número por 0,0025 equivale a
0,3001
,para a =
0
R:
16)
2
22) O valor de E = 5  2
R: 160km/h
R: 400
expressão
9 5
4 2
Pedrão observou que um veículo estava andando a
da
17
16
b=
14) Assistindo a um filme de ação norte-americano,
valor
 1
 1
−3
0
  +   − 2 + 16 é:
2
4
 
 
R:
13) Um carro que anda a uma velocidade de 80km/h,
PROF PEDRÃO
125
6
Neste curso os melhores alunos estão sendo preparados pelos melhores Professores
3
MATEMÁTICA
SATVIRTUA
27) O valor da expressão
PROF PEDRÃO
EXERCÍCIOS
4.(0,5 )3 + 0,25 − 2 −2 ,
é:
31) Eduardo e Mônica eram dois colegas de repartição
3
R:
4
num dia de trabalho e, em um dos poucos momentos
de tranqüilidade resolveram brincar de adivinhações
28) Efetue as operações indicadas em cada item,
com números inteiros positivos.
E – Mônica, pense em um número.
apenas deslocando a posição da vírgula no numeral.
M – Já pensei.
a) 13,57 x 100
E – Multiplique esse número por 10.
b) 17,45 : 100
c) 0,008 x 10
d) 523,4 : 10
R: a) 1357
M – Pronto.
4
E – Agora subtraia o número pensado do
2
b) 0,1745
c) 80
resultado obtido.
d)5,234
M – Já subtraí.
E – Some 180 ao novo rersultado.
-2
29) O resultado mais simples da expressão: (10 :
M – Somei.
0,001) x (2/5 - 0,04) é
E – Finalmente, divida o último resultado obtido
18
R:
5
por 9.
M – Pronto.
2
30) O valor de
E – Quanto deu?
0,00001 ⋅ (0,01) ⋅ 10000
0,0001
M – Deu 68!
Qual o número que Mônica pensou?
R: 0,1
R: 48
32) A solução da equação:
EQUAÇÕES DO 1º GRAU
Uma equação na variável x é dita do 1º grau
– 3(x – 1) – (2x – 2) = 0 é:
R: 01
quando se apresenta na forma
33) O valor de x que é solução da equação
ax + b = 0
Sendo a e b reais e a ≠ 0.
1 1 1
x
é:
+ + =
2 3 4 48
A resolução de uma equação do 1º grau consiste
R: 52
em isolar a variável no 1º membro, determinando
34)
assim o seu valor.
Para
resolvermos
uma
equação
podemos
adicionar, subtrair, multiplicar ou dividir os dois
membros da igualdade, obtendo uma nova igualdade
O
valor
de
x
na
equação
x + 6 x + 8 x + 10 1 − x
vale:
−
=
−
2
6
4
3
R: – 2
equivalente à primeira, ou seja, com a mesma
solução.
35)
x−2+
4
2009
A
raiz
da
2(x − 1) 2(x − 3 ) 2
=
− vale: R: 00
5
3
5
Neste curso os melhores alunos estão sendo preparados pelos melhores Professores
equação
MATEMÁTICA
SATVIRTUA
36) João gasta 1/4 do seu salário na prestação de sua
PROF PEDRÃO
SISTEMAS DE EQUAÇÕES DO 1º GRAU
casa, 3/5 do restante ele gasta com alimentação,
A solução de um sistema de equações pode ser
sobrando-lhe ainda a quantia de R$300,00. qual o
obtida utilizando-se diversos métodos, sendo que para
valor do salário de João?
os sistemas de duas equações a duas variáveis
R: R$ 1000,00
utilizamos,
com
mais
freqüência,
utilizamos os
métodos da adição e da substituição.
37) No mês passado, gastei um terço do meu salário
Vamos resolver os seguintes sistemas:
com alimentação, 40% com aluguel, R$ 500,00 com
despesas eventuais e sobraram R$ 300,00. Qual foi o
x − 2 y = 3
2 x − 3 y = 5
a) 
meu salário?
R: R$ 3000,00
38) Dos aprovados em um concurso, o número de
homens é igual a 4/3 do número de mulheres. Em um
primeiro chamado, foram dispensados 16 homens e 4
mulheres, ficando o número de homens igual ao
número de mulheres. Qual o número total de homens
2 x + 5 y = 7
3 x − 4 y = −1
b) 
e de mulheres que foram aprovados no concurso?
R: 36 mulheres e 48 homens
39) Uma pessoa resolveu calcular quanto gastaria
com refeições por mês. Verificou que, se gastasse
R$8,00 por refeição, poderia fazer 3 refeições a mais
EXERCÍCIOS
do que se gastasse R$10,00. Calcule quanto essa
pessoa possuía.
41) Um atirador deveria receber 4 reais por tiro
R: R$120,00
acertado no alvo e pagar a metade cada vez que
40) A quantidade de acidentes registrados com carros
errasse. Depois de 32 tiros, recebeu 86 reais. Quantos
de passeio e caminhões em um trecho de uma BR em
tiros acertou?
um determinado período foi tal que a quantidade de
R: 25
acidentes com carros foi igual a quantidade de
acidentes com caminhões mais 15 e o dobro da
42) Um taxista trocou uma nota de 50 reais por notas
quantidade de acidentes com carros foi igual ao triplo
de 2 reais e 5 reais num total de 19 notas. Quantas
da quantidade de acidentes com caminhões. Calcule a
notas de cada valor o taxista recebeu?
quantidade de acidentes que ocorreu com cada tipo
R: 4 notas de R$ 5,00 e 15 notas de R$ 2,00
de veículo.
R: carros = 45 e caminhões = 30
43) Em um estacionamento para veículos apreendidos
há 30 veículos entre motos e carros. Sendo o total de
rodas igual a 82, quantos são os veículos de cada
tipo?
R: 19 motos e 11 carros
2009
Neste curso os melhores alunos estão sendo preparados pelos melhores Professores
5
MATEMÁTICA
SATVIRTUA
PROF PEDRÃO
44) O Sr. Pedrão é dono de uma pequena fazenda, a
qual é administrada pelo filho dele, Pedro. Pedro gosta
de fazer algumas brincadeiras com o pai. No fim do
mês, Pedro sempre deve dar um relatório
do andamento da fazenda. O relatório deste mês foi o
seguinte: “Entre porcos e galinhas consegui contar
1000 patas e 300 cabeças”.
Quantos porcos e
quantas galinhas há exatamente na fazenda do Sr.
Pedrão?
R: 200 porcos e 100 galinhas
45) Para se deslocar de casa até o seu trabalho, uma
pessoa percorre 550 km por mês. Para isso, em
alguns dias, ele utiliza um automóvel e, em outros,
uma motocicleta. Considerando que o custo do
quilômetro rodado é de 21 centavos para o automóvel
e de 7 centavos para a motocicleta, calcule quantos
quilômetros a pessoa deve andar em cada um dos
veículos, para que o custo total mensal seja de
R$70,00.
R: 225km com o carro e 325km com a moto
46) Um policial rodoviário aplicou durante uma “blitz”
apenas dois tipos de multa, num total de 80, sendo
que o valor arrecadado será de R$ 4300,00. Cada
multa do tipo A custa R$ 50,00 e cada multa do tipo B
custa R$ 60,00. Quantas multas de cada tipo ele
aplicou?
R: 50 do tipo A e 30 do tipo B
47) Um pacote tem 62 balas, algumas de uva e as
demais de laranja. Se a terça parte do dobro do
número de balas de uva excede a metade do
número de balas de laranja em 4 unidades, então,
nesse pacote há quantas balas de cada tipo?
R: 32 de laranja e 30 de uva
48) Deseja-se pintar duas fileiras de cinco quadrados
num muro retangular de 5 metros de comprimento por
2,2 metros de altura, conforme a figura a seguir.
6
2009
Os lados dos quadrados serão paralelos às laterais do
muro e as distâncias entre os quadrados e entre cada
quadrado e a borda do muro serão todas iguais.
Nessas condições, a medida do lado de cada
quadrado, em metros, será:
R: 0,6m
49) Uma fábrica de doces vende caixas com 50
unidades de bombons recheados com dois sabores,
morango e caramelo. O custo de produção dos
bombons de morango é de 10 centavos por unidade,
enquanto o dos bombons de caramelo é de 20
centavos por unidade. Os demais custos de produção
são desprezíveis. Sabe-se que cada caixa é vendida
por R$ 7,20 e que o valor de venda fornece um lucro
de 20% sobre o custo de produção de cada bombom.
O número de bombons de cada sabor contidos em
uma caixa é igual a:
R: 10 de caramelo e 40 de morango
50) Pafúncio, Estrupício e Emingarda foram a uma
lanchonete. Pafúncio comeu 3 pastéis e tomou dois
sucos, pagando R$9,00 pelo lanche; Estrupício comeu
2 pastéis e tomou um refrigerante, pagando R$6,00
pelo lanche; Emingarda comeu um pastel e tomou
dois sucos, pagando R$5,00 pelo lanche. Sabendo
que todos pagaram os valores certos de cada item,
então podemos afirmar que um pastel e um suco
custam o mesmo que dois refrigerantes.
R: Falso
51) Emingarda será madrinha de casamento de sua
irmã e pretende presenteá-la com artigos de cozinha.
Na primeira loja por ela visitada, o preço de um
conjunto que tem 3 panelas, 2 frigideiras e 1 leiteira é
de R$ 169,00; na segunda loja visitada, o preço de um
conjunto composto por 4 panelas, 1 frigideira e 1
Neste curso os melhores alunos estão sendo preparados pelos melhores Professores
MATEMÁTICA
SATVIRTUA
PROF PEDRÃO
leiteira é de R$ 179,00; na terceira loja visitada o
RAZÃO
preço de um conjunto com 3 panelas, 1 frigideira e 1
leiteira é de R$ 144,00. Se o preço de
cada panela, da frigideira e da leiteira é o mesmo em
É uma divisão:
a
b
todas as lojas por ela visitada, então pode-se afirmar
que o preço de um conjunto composto por 4 panelas,
PROPORÇÃO
2 frigideiras e 1 leiteira é igual a:
R: R$ 204,00
É a igualdade entre razões:
a c
=
b d
52) Pedrão entrou numa lanchonete e pediu 3
hambúrgueres, 1 suco de laranja e 2 cocadas,
GRANDEZAS DIRETAMENTE PROPORCIONAIS
gastando R$ 21,50. Na mesa ao lado, algumas
Têm “o mesmo sentido” de variação – quando uma
pessoas pediram 8 hambúrgueres, 3 sucos de laranja
aumenta, a outra também aumenta ou quando uma
e 5 cocadas, gastando R$ 57,00. Sabendo-se que o
diminui, a outra também diminui.
preço de um hambúrguer, mais o de um suco de
laranja, mais o de uma cocada totaliza R$ 10,00,
calcule o preço de cada um desses itens.
GRANDEZAS INVERSAMENTE PROPORCIONAIS
Têm “sentidos contrários” de variação – quando uma
R: hambúrguer R$ 4,00; cocada R$ 3,50; suco R$
aumenta, a outra diminui ou quando uma diminui a
2,50
outra aumenta.
53) Uma herança de R$ 270.000,00 foi distribuída
EXERCÍCIOS
entre 3 irmãs, de modo que a filha do meio recebeu
metade do que recebeu a filha mais nova e a mais
55) Uma operadora de telefone celular cobra uma
velha recebeu o equivalente à metade do que
tarifa de R$ 0,40 por minuto de ligação e uma de
receberam juntas a mais nova e a do meio. Em reais,
telefone fixo, R$ 0,16 pelo pulso de 4 minutos.
a filha mais velha recebeu:
Comparando-se os dois valores, conclui- se que a
R: R$ 90.000,00
razão entre a tarifa do celular e a do fixo é:
R:10
54) Uma conta no valor de R$ 195,00 foi paga com
cédulas de dois, cinco, dez e de vinte reais,
56) Paulo e André receberam juntos R$88.000,00.
totalizando 30 cédulas. Juntando-se as cédulas de
Enquanto Paulo aplicou 3/5 do que recebeu em ações,
cinco com as de dez reais usadas no pagamento,
André investiu 2/3 de sua parte na montagem de uma
obteve-se um total de dez cédulas, e a quantidade das
pequena empresa. Após essas duas operações,
cédulas de vinte reais usadas foi de um terço do
ambos ficaram com quantias iguais. Com base nessas
número de cédulas de dois reais. A quantidade de
informações, é correto afirmar que o valor investido
cédulas de cinco reais usadas para o pagamento da
por André, em reais, é igual a:
conta foi de:
R:32.000
R: 7
2009
Neste curso os melhores alunos estão sendo preparados pelos melhores Professores
7
MATEMÁTICA
SATVIRTUA
PROF PEDRÃO
57) Antônio aplicou a quantia de R$ 800,00 e Carolina
aplicou a quantia de R$ 400,00. Essas duas
aplicações,
feitas
em
uma
mesma
REGRA DE TRÊS COMPOSTA
Quando há mais que duas “situações” envolvidas.
instituição
Pode ser diretamente ou inversamente proporcional,
financeira, renderam juntas, após certo período, R$
inclusive misturando as situações em uma mesma
600,00. Nessas condições, a aplicação de Antônio e a
questão.
de Carolina renderam, respectivamente:
R:R$ 400,00 e R$ 200,00
EXERCÍCIOS
58) Cecília presenteou seus netos, André de 8 anos e
62) Em uma pesquisa sobre o analfabetismo em
Sofia de 6 anos, com a quantia de R$420,00 dividida
matemática,
em partes proporcionais a suas idades. A quantia
amostra que representa 110 milhões de brasileiros
recebida por Sofia, em reais, foi:
entre 15 e 64 anos de idade. Dentre os entrevistados,
R: 180
60 foram considerados analfabetos absolutos em
foram
entrevistadas
2000
pessoas,
matemática. Com base nas informações do texto
59) Uma herança de R$ 40.000,00 será dividida entre
acima, calcule o número estimado de brasileiros entre
três irmãos A, B e C, em partes proporcionais às suas
15 e 64 anos, analfabetos absolutos em matemática.
idades 5, 8 e 12, respectivamente. A quantia que B irá
R: 3 300 000
receber é
63) De acordo com reportagem da revista Veja (20 de
R: R$ 12.800,00
junho de 2007, p. 88-90), um dos grandes sonhos da
60) Três sócios A, B e C montaram um negócio, sendo
classe
média
que A investiu R$ 8.000,00, B investiu R$ 6.000,00 e
economicamente ativa é passar em um concurso
C investiu R$ 4.000,00. Eles combinaram que o lucro
público. A proporção de funcionários públicos entre os
obtido seria dividido proporcionalmente aos capitais
trabalhadores “formais” no Brasil passou de 17%, na
investidos. Após algum tempo, verificou-se um lucro
década de 80, para 22%, atualmente. Segundo dados
de R$ 7.200,00, a ser distribuído. Pode-se afirmar que
do
os valores a serem atribuídos a A, B e C são,
aproximadamente 9 milhões de cidadãos. De acordo
respectivamente:
com esses dados, calcule a quantidade aproximada
R: R$ 3.200,00; R$ 2.400,00 e R$ 1.600,00
de trabalhadores na iniciativa privada atualmente. R:
IBGE,
o
brasileira
Estado
que
começa
brasileiro
a
emprega
vida
hoje
31,9
61) Dividindo 264 em três partes inversamente
proporcionais a 2, 5 e 8, encontramos três números
64) Um feirante vende uma dúzia de laranjas por
cuja soma dos dois maiores é igual a S. Calcule S.
R$1,50. Se um cliente comprar 20 laranjas, quanto ele
R:S = 160 + 64 = 224
irá pagar ao feirante?
R:R$ 2,50
REGRA DE TRÊS SIMPLES
Quando há apenas duas “situações” envolvidas.
Pode ser diretamente ou inversamente proporcional.
65) Se, em uma fábrica de automóveis, 12 robôs
idênticos fazem uma montagem em 21 horas, em
quantas horas 9 desses robôs realizam a mesma
tarefa? R: 28 horas
8
2009
Neste curso os melhores alunos estão sendo preparados pelos melhores Professores
MATEMÁTICA
SATVIRTUA
PROF PEDRÃO
66) Um festival foi realizado num campo de 240m por
71) Se 6 pessoas, trabalhando 4 horas por dia,
45m. Sabendo que para cada 2 m2 havia, em média,
realizam um trabalho em 15 dias, 8 pessoas,
7 pessoas, quantas pessoas havia no festival?
trabalhando 6 horas por dia, farão o mesmo trabalho
R: 37.800
em: R: 7,5 dias
67) Em 2006, segundo notícias veiculadas na
72) Um fabricante de queijo gasta 60 litros de leite
imprensa, a dívida interna brasileira superou um
para fazer 18 queijos de 2,5kg cada um. Quantos
trilhão de reais. Em notas de R$ 50,00, um trilhão de
queijos de 2kg ele faz com 80 litros de leite?
reais tem massa de 20.000 toneladas. Com base
R: 30 queijos
nessas informações, pode–se afirmar corretamente
que a quantidade de notas de R$ 50,00 necessárias
73) Ao reimprimir um livro de 100 páginas de 32 linhas
para pagar um carro de R$ 24.000,00 tem massa, em
com 42 letras por linha, usaram-se 24 linhas de 32
quilogramas, de
letras. O novo livro foi apresentado com:
R: 0,48
R: 175 páginas
68) Se o vazamento de uma torneira enche um copo
de 200ml de água a cada hora, é correto afirmar que,
para se desperdiçar 3m3 de água, são necessários
R: 625 dias
PORCENTAGEM
É sempre uma regra de três simples, diretamente
proporcional.
comprimento usada em Nanotecnologia (“nano” vem
30
= 0,30
100
3
3% =
= 0,03
100
do grego e significa “anão”). Sabe-se que um metro
Ex:
equivale a um bilhão de nanômetros.
a) Calcule 10% de 20%
30% =
69) O nanômetro é a unidade de medida de
Considerando o diâmetro da Terra com 13.000
quilômetros, conclui-se que a medida do diâmetro da
terra, em nanômetro, é igual a
R: 1,3 x 10
2
b) Calcule (10%)
16
70) Para escaparem de uma penitenciária, 10
c) Calcule
100 %
prisioneiros decidem cavar um túnel de 450m de
comprimento. Em uma fuga anterior, 12 prisioneiros
cavaram um túnel de 270m, trabalhando 6 horas por
74) Um comerciante reajustou o preço de determinado
noite, durante 9 noites. Se os atuais prisioneiros
produto em 10%. Observando que as vendas caíram,
pretendem trabalhar 4 horas por noite, em quantas
resolveu dar um desconto de 10% sobre o valor
noites o túnel ficará pronto?
anunciado para o produto. Podemos afirmar que o
R: 27
valor final, em relação ao inicial, será:
R: 99% do valor inicial
2009
Neste curso os melhores alunos estão sendo preparados pelos melhores Professores
9
MATEMÁTICA
SATVIRTUA
PROF PEDRÃO
75) A população de uma cidade cresceu 25% em um
80) Segundo dados publicados na revista Istoé
ano e, no ano seguinte, teve um decrescimento de
Dinheiro (02/08/06) no ano de 2006 deverão ser
25%. Em relação à população inicial da cidade,
investidos no mundo 673 bilhões de dólares em mídia
podemos deduzir corretamente que a população:
e serviços de marketing. Este valor representa um
R: diminuiu 6,25%
crescimento de 6,2% em relação a 2005. Com base
nesses dados, calcule quanto foi investido no mundo,
76) Um cliente possui R$ 100,00 (cem reais) em sua
no ano de 2005, em mídia e serviços de marketing.
conta bancária. Sabendo-se que o Governo Federal
R: 633,71 bilhões de dólares
cobra um tributo de 0,38% de CPMF (Contribuição
Provisória sobre a Movimentação Financeira) sobre
81) João, no primeiro trecho de sua caminhada,
cada movimentação financeira, qual o valor máximo
percorreu 12% de uma estrada. Ao concluir o segundo
que esse cliente pode sacar sem ficar com a conta
trecho, correspondente a 1.200 metros, o percentual
negativa?
percorrido passou a ser 16% da estrada. A extensão
R: R$99,62
da estrada é
R: 30 km
77) Um administrador municipal promoveu uma
consulta à população com o objetivo de obter
82) Um comerciante comprou uma peça de tecido de
subsídios para o projeto do orçamento do próximo
100m por R$ 900,00. Se ele vender 40m com lucro de
ano. Das pessoas consultadas, 4392 responderam
35%, 50m com lucro de 20% e 10m pelo preço de
que a maior prioridade deveria ser dada à segurança
custo, então o comerciante terá um lucro na venda da
pública. Sabendo que estas constituíam 24% do total
peça de: R: 24%
de pessoas consultadas, calcule esse total.
83) O dono de uma loja sabe que, para não ter
R: 18.300
prejuízo, o preço de venda de determinado produto
78) Em uma turma de alunos que estudam Geometria,
deve ser, no mínimo, 30% superior ao preço de custo.
há 100 alunos. Dentre estes, 30% foram aprovados
Visando atender clientes que pedem desconto, o dono
por média e os demais ficaram em recuperação.
da loja define o preço de venda, acrescentando 60%
Dentre os que ficaram em recuperação, 70% foram
ao preço de custo. Dessa forma, o maior desconto que
aprovados.
ele pode conceder, sem ter prejuízo, é de:
Determine
o
percentual
de
alunos
aprovados nessa disciplina.
R: 18,75%
R: 79%
84) Francisco resolveu comprar um pacote de viagem
79)
Pedrão
comprou
dois
aparelhos
de
ar
que custava R$4200,00,
já incluídos R$120,00
condicionado e, com isso, seu consumo de energia
correspondentes a taxas de embarque em aeroportos.
elétrica, de setembro para outubro, cresceu em 40%.
Na agência de viagens, foi informado de que, se
Se a conta de outubro registra um consumo de
fizesse o pagamento à vista, teria um desconto de
210kWh, a conta de setembro registrava um consumo
10%, exceto no valor referente às taxas de embarque,
de:
sobre o qual não haveria nenhum desconto. Decidiu,
R: 150kWh.
pois, pagar o pacote de viagem à vista. Então, é
CORRETO afirmar que Francisco pagou por esse
pacote de viagem: R: R$3792,00
10
2009
Neste curso os melhores alunos estão sendo preparados pelos melhores Professores
MATEMÁTICA
SATVIRTUA
PROF PEDRÃO
85) Em porcentagem das emissões totais de gases do
disso, o aluguel e o IPTU consomem juntos 20% do
efeito estufa, o Brasil é o quarto maior poluidor,
seu salário e 1/4 do que recebe é gasto com
conforme a tabela abaixo. É CORRETO afirmar que a
alimentação e a compra de produtos de primeira
porcentagem de gases emitidos juntamente por Japão
necessidade. Com base nessas informações, é
e Canadá, em relação aos gases emitidos pelo Brasil,
correto
é aproximadamente: R: 92,6%
condições de poupar:
Classifica ção
País
Porcentage m
1º
Estados Unidos
15,8
2º
4º
China
Brasil
11,9
5,4
7º
Japão
3,2
9º
10 º
Malásia
Canadá
2,1
1,8
afirmar
que,
mensalmente,
Jorge
tem
R: R$54,00
90) Joana, que trabalha como vendedora, teve duas
propostas de emprego:
- a primeira oferece um salário de R$ 600,00, mais
comissão de 1% do seu total de vendas;
- a segunda oferece um salário de R$ 700,00, mais
comissão de 0,6% do seu total de vendas.
86) Mona verificou que o preço de um televisor era R$
Acima de qual valor total de vendas efetuadas, a
840,00. Após uma semana, retornou à mesma loja e
primeira proposta de emprego de Joana oferece maior
constatou que o preço da mesma televisão fora
salário do que a segunda?
reajustado em mais 15%. O desconto que Mona deve
R: R$25000,00
receber para que o valor da televisão retorne ao preço
anterior é, aproximadamente, de:
91) O preço de um carro novo é de R$ 22.000,00 e
R: 13%
diminui de 10 % a cada ano de uso. Qual será o preço
com 3 anos de uso?
87) Uma empresa comprou três milhões de reais em
dólares.
No
primeiro
mês,
o
dólar
R: R$ 16.038,00
oscilou
negativamente em 12%, mas no segundo mês a
92) Um vendedor de frutas levava um carregamento
empresa
de caixas de laranjas para vender a seu cliente a R$
conseguiu
recuperar
8%
do
prejuízo
acumulado. Ao final do segundo mês, a perda da
8,40 cada caixa. Ao chegar para a venda percebeu
empresa em relação ao seu investimento inicial foi de
que havia doze caixas com frutas impróprias para o
aproximadamente:R: 11%
consumo, que foram descartadas, e as que sobraram
foram vendidas por ele com acréscimo de 15% em
88) Um investidor iniciante investiu R$ 3.000,00 na
seu preço. Com isso, obteve o mesmo montante que
Bolsa de Valores. No primeiro mês ele perdeu 40% do
conseguiria caso não tivesse perdido as doze caixas e
valor investido e no segundo mês ele recuperou 30%
as tivesse vendido a R$ 8,40. A quantidade de caixas
do prejuízo do mês anterior. Ao final do segundo mês,
de laranjas vendidas foi de:
o montante investido em sua carteira era de:R:
R: 80
R$2160,00
93) Recentemente o governo autorizou um aumento
89) Jorge trabalha em uma empresa cujo piso salarial
de 10% no preço da gasolina e, logo em seguida, um
é de R$360,00 e recebe, mensalmente, o triplo desse
aumento de 8% no preço do álcool. Como, na
valor. A metade do que ganha fica comprometida com
composição da gasolina, o álcool contribui com 25%, o
as despesas de luz, gás, transporte e lazer. Além
preço da gasolina teve, então, um novo reajuste
2009
Neste curso os melhores alunos estão sendo preparados pelos melhores Professores
11
MATEMÁTICA
SATVIRTUA
PROF PEDRÃO
correspondente ao aumento do preço do álcool. O
98) Consideremos a renda per capita de um país
aumento da gasolina, levando em conta os dois
como a razão entre o Produto Interno Bruto (PIB) e
reajustes, foi de:
sua população. Em 2004, a razão entre o PIB da
R: 12,2%
China e o Brasil, nesta ordem, era 2,8; e a razão entre
suas populações, também nesta ordem, era 7. Com
94) A tabela abaixo descreve os valores gastos, no
base
primeiro ano de vida, com cachorros e gatos. De
corretamente que, em 2004, a renda per capita do
acordo com a tabela, para um cachorro e um gato, o
Brasil superou a da China em
gasto com ração, no primeiro ano, representa em
a) menos de 50%
relação ao custo total, incluindo o preço dos animais, a
b) exatamente 50%
porcentagem de: R: 24%
c) exatamente 100%
nessas
informações,
pode–se
afirmar
d) exatamente 150%
e) mais de 150%
99) Com o reajuste de 10% no preço da mercadoria A,
seu novo preço ultrapassará o da mercadoria B em R$
9,99. Dando um desconto de 5% no preço da
mercadoria B, o novo preço dessa mercadoria
se igualará ao preço da mercadoria A antes do
95) Quando foi admitido em uma empresa, José
reajuste de 10%. Assim, o preço da mercadoria B,
contratou um plano de saúde, cujo valor correspondia
sem o desconto de 5%, em R$, é:
a 5% do seu salário. Hoje, José tem um salário 30%
R: R$222,00
maior e o plano de saúde teve, desde a admissão de
José,
um
aumento
de
82%,
representando,
100) De acordo com diagnóstico do Banco Central a
atualmente, K% do salário de José. O valor de K é:
respeito de meios de pagamento de varejo no Brasil,
R: 7%
no
ano
de
2006,
constata-se
que
24%
dos
pagamentos foram feitos com cheque e 46%, com
96) Um teatro aumenta o preço do ingresso em 8%.
cartão. O valor médio desses pagamentos foi de R$
Em conseqüência, o número de ingressos vendidos
623,00 para os cheques e de R$ 65,00 para os
diminui em 5%. Qual é a variação, em porcentagem,
cartões. O valor médio, quando se consideram todos
da receita obtida pelo teatro?
os pagamentos efetuados com cheque e cartão, é,
R: 2,6%
aproximadamente,
R: R$ 256,00.
97) O preço do produto X é 20% menor que o do
produto Y, e este, por sua vez, tem preço 20% maior
que o do produto Z. Se os preços dos três produtos
somam R$ 237,00, quanto custa, em reais, o produto
Z?
R: R$75,00
12
2009
Neste curso os melhores alunos estão sendo preparados pelos melhores Professores
MATEMÁTICA
SATVIRTUA
JUROS SIMPLES
PROF PEDRÃO
107) A que taxa mensal o capital de R$ 1.200,00, no
fim de dois meses, geraria um capital acumulado de
j = c.i.t
R$2.400,00?
R: 50%
j = juros, c = capital, i = taxa, t = tempo
108) Durante quantos meses um capital de R$ 100,00,
MONTANTE
aplicado a uma taxa de 30% a.m., geraria um
montante de R$ 220,00?
M=c+j
M = montante, j = juros, c = capital
R: 04
109) Qual é o prazo para uma aplicação de 5% a.a.,
tenha um aumento que corresponda a 1/5 de seu
EXERCÍCIOS
valor?
R: 4anos
101) Calcular os juros simples que um capital de R$
10.000,00, rende em um ano e meio, aplicado à taxa
110) Em quanto tempo um capital aplicado à taxa de
de 6%a.a.?
150% a.a., quadruplique seu valor?
R: R$900,00
R: 2anos
102) Qual o capital que produz, à taxa de 6% a.a., em
111) Um capital de R$ 14.400,00, aplicado a 22% a.a.,
3 meses, juro de R$ 78,00?
rendeu R$ 880,00 de juros. Durante quanto tempo
R: R$5200,00
esteve empregado?
R: 3meses e 10dias
103) A que taxa anual o capital de R$ 5.000,00, em 1
ano, renderia R$ 300,00?
112) Calcule o valor do montante produzido por capital
R: 6%
de 150, aplicado a juro simples a uma taxa de 4,8%
a.m. , durante 25 dias?
104) Durante quantos meses um capital de R$ 100,00
R: 156
aplicado a uma taxa de 30% a.m., renderia R$
240,00?
113) José colocou 2/3 de meu capital a 36% a.a., e o
R: 8
restante a 18% a.a., recebendo juro anual de
R$117.000,00. Qual é o meu capital?
105) Calcule o montante produzido por capital de R$
R: R$390000,00
5.000,00, aplicado durante 3 meses a uma taxa de
15% a.m?
R: R$7250,00
106) Qual o capital que em dois anos, à taxa de 5%
a.a., produz um montante de R$ 6.600,00?
R: R$6000,00
2009
Neste curso os melhores alunos estão sendo preparados pelos melhores Professores
13
MATEMÁTICA
SATVIRTUA
JUROS COMPOSTOS
PROF PEDRÃO
119) A que taxa de juros compostos R$ 560.000,00
devem ser aplicados para produzirem o montante de
MONTANTE
R$ 888.608,00 em 6 meses de aplicação?
R: 8%a.m.
M=c+j
M = c.(1+i)t
M = montante, j = juros, c = capital, i = taxa,
t = tempo
EQUAÇÕES DO 2º GRAU
Uma equação na variável x é dita do 2º grau
quando se apresenta na forma:
ax2 + bx + c = 0
EXERCÍCIOS
114) O capital de R$ 500.000,00 e aplicado à 5% a.m.
de juros compostos, durante 3 meses. Calcule o
Sendo a, b e c reais e a ≠ 0.
A resolução de uma equação do 2º grau pode ser
feita utilizando a fórmula de Bháskara:
montante?
R: R$578800,00
x=
−b± ∆
2a
→
∆ = b 2 − 4ac
115) Calcule o capital que produz o montante de R$
112.360,00, à taxa de 6% a.m. de juros compostos
durante 2 meses é:
Alguns casos particulares de resolução ocorrem
quando b = 0 e/ou c = 0.
R: R$100000,00
Um método bastante utilizado é o de soma e
produto. Uma equação do 2º grau pode ser escrita,
116) Qual o valor do capital que aplicado a 4% a.m. de
em função da soma e do produto de suas raízes, da
juros compostos, produz ao final de 5 meses, um
seguinte forma:
montante de R$ 1.300.000,00?
2
1x – Sx + P = 0
R: R$1068463,87
117) Durante quantos meses o capital R$ 500.000,00
deverá ser aplicado a 6% a.m. de juros compostos
para se transformar em R$ 844.700,00?
b

S = x1 + x 2 = − a
Onde: 
P = x ⋅ x = c
1
2
a

R: 09
Resolva as equações:
118) Quantos bimestres são necessários para o
capital R$ 1.000.000,00 se transformar em R$
120) 2x – 5x + 2 = 0
3.341.700,00, se for aplicado a 9% a.m. de juros
R: x1 = 1/2 x2 = 2
2
compostos?
R: 7
121) 2x2 – 6x = 0
R: x1 = 0 x2 = 3
14
2009
Neste curso os melhores alunos estão sendo preparados pelos melhores Professores
MATEMÁTICA
SATVIRTUA
PROF PEDRÃO
2
122) 2x – 18 = 0
UNIDADES DE COMPRIMENTO
R: x1 = – 3 x2 = 3
km hm dam m dm cm mm
2
123) 3x = 0
130) Transforme:
R: x1 = x2 = 0
a) 2,5km para m
2
124) x – 7x + 12 = 0
b) 1,70m para cm
R: x1 = 3 x2 = 4
c)1765m para km
d) 25cm para dm
125) A soma dos possíveis valores de x que verificam
−
2
x
4
=
5
1
x
a igualdade
−
R: a) 2500m b) 170cm c) 1,765km d) 2,5dm
é:
UNIDADES DE ÁREA
R: 03
126) A soma e o produto das raízes da equação
2
km
2
2
hm
dam
2
m
2
dm
2
cm
2
mm
x2 – x + 1 = 0 valem:
131) Transforme:
R: S = 1 e P = 1
a) 2,5km2 para m2
2
2
127) Considere um número cujo quadrado menos
b) 1,70m para cm
seus dois terços resulta 7. Há dois números que
c) 1765m para km
obedecem a essas condições. Quais são esses
d) 25cm2 para dm2
números?
R: a) 2500000m² b) 17000cm² c) 0,001765km² d)
R: x1 = – 7/3 x2 = 3
0,25dm²
2
2
128) A soma e o produto das idades em anos de dois
UNIDADES DE VOLUME
amigos valem, respectivamente, 40 e 396. A idade em
anos do mais jovem é:
3
km
R: 18
3
3
hm
dam
3
m
3
dm
3
cm
129) Todos os funcionários de uma empresa irão
132) Transforme:
contribuir igualmente para fazer um bolão da Mega
a) 2,5m para dm
Sena, cujo valor é R$2700,00. Na hora de recolher o
b) 1,574m para cm
dinheiro para fazer o bolão, dois funcionários da
c) 6540dm para m
empresa desistiram de participar e, com isso, a cota
R: a) 2500dm³ b) 1574000cm³ c) 6,54m³
3
3
3
3
3
mm
3
3
que cada participante deveria pagar sofreu um
aumento de R$8,00, para manter o valor total do
bolão. Dessa forma, calcule o número total de
funcionários dessa empresa.
1m 3 = 1000l
Lembre-se:
1dm 3 = 1l
1cm3 = 0,001l = 1ml
R: 27
2009
Neste curso os melhores alunos estão sendo preparados pelos melhores Professores
15
MATEMÁTICA
SATVIRTUA
d
a
r
c)
2 3
e) 120º
π
4
b)
d
a
r
3
b) 45dm para litros
π
6
R: a)
a) 2,5m3 para litros
d
a
r
133) Transforme:
PROF PEDRÃO
d) 135º
f) 300º
3
c) 52cm para litros
R: a) 2500litros b) 45litros c) 0,052litros
136) Nos X-Games Brasil, em maio de 2004, o
skatista brasileiro Sandro Dias, apelidado "Mineirinho",
conseguiu realizar a manobra denominada "900", na
UNIDADES DE MASSA
modalidade skate vertical, tornando-se o segundo
atleta
kg
hg
dag
g
dg
cg
mg
no
mundo
a
conseguir
esse
feito.
A
denominação "900" refere-se ao número de graus que
o atleta gira no ar em torno de seu próprio corpo, que,
134) Transforme:
no caso, corresponde a:
a) 1,250kg para g
a) uma volta completa.
b) 3g para mg
b) uma volta e meia.
c) 510g para kg
c) duas voltas completas.
R: a) 1250g b)3000mg c) 0,51kg
d) duas voltas e meia.
e) cinco voltas completas
R: d)
UNIDADES DE ÂNGULO
SUBMÚLTIPLOS DO GRAU
CÍRCULO
1º = 60’
TRIGONOMÉTRICO
1’ = 60’’
137) No último pleito, o horário de encerramento das
votações, segundo determinação do TSE para todo o
estado do Paraná, foi às 17 horas. Passados 5
minutos do encerramento, o menor ângulo entre os
ponteiros do relógio era de:
R: 122º 30´
UNIDADES DE TEMPO
135) Transforme:
1h = 60min
a) 30º para radianos
1min = 60seg
b) 45º para radianos
c) 60º para radianos
d)
3π
rad para graus
4
2π
e)
rad para graus
3
5π
f)
rad para graus
6
16
2009
138) Dois veículos partem simultaneamente de uma
mesma subestação, percorrendo rotas diferentes. O
primeiro retorna ao ponto de partida a cada 40 min e o
segundo, a cada 50 min. Se ambos saíram às 20h,
que
horas
eles
estarão
novamente
juntos
subestação?
R: 23h20min
Neste curso os melhores alunos estão sendo preparados pelos melhores Professores
na
MATEMÁTICA
SATVIRTUA
PROF PEDRÃO
UNIDADES DE VELOCIDADE
139) Um carro que anda a uma velocidade de 80km/h,
(
=
3
n 2
n
R: 22,22m/seg
Diagonais
d
está andando, em m/seg, a uma velocidade de:
POLÍGONOS
−
)
Soma dos ângulos
140) Assistindo a um filme de ação norte-americano,
(
2
n
O
0
8
1
=
−
)
o
0
6
3
e
R: 160km/h
S
equivale, em km/h, a uma velocidade igual a:
=
Externos
i
uma velocidade de 100 milhas por hora, o que
S
Pedrão observou que um veículo estava andando a
Internos
Regulares
i
o
e
e
0
6n
3
=
Sn
a
TEOREMA DE TALES
Sn
=
i
a
GEOMETRIA PLANA
=
SEMELHANÇA DE TRIÂNGULOS
a b c
= = = cons tan te
x y z
141) Na figura abaixo, fora de escala, M representa o
=
zc
yb
+
+
xa
=
yb
=
xa
zc
yb
xa
=
+
+
+
+
= ⋅⋅⋅
141) Na figura abaixo, o valor em graus de x e y é:
ponto a 12 metros do solo, na janela de um
apartamento, de onde uma senhora pode observar o
seu filho embarcar no ônibus escolar no ponto P, a
100 metros do prédio em que moram. Um muro está
sendo construído, à distância de 35 metros da fachada
do mesmo prédio. Qual a altura mínima do muro para
que a senhora perca a visibilidade do ponto P?
R: x = 63o e y = 89o
R: 7,8m
2009
Neste curso os melhores alunos estão sendo preparados pelos melhores Professores
17
MATEMÁTICA
SATVIRTUA
142) Na figura abaixo, ABCD é um trapézio com base
PROF PEDRÃO
ÁREA DOS PRINCIPAIS POLÍGONOS
maior medindo 40 cm, base menor medindo 25 cm e
altura 30 cm. Prolongando os lados AD e BC, obtém-
TRIÂNGULOS
se o ponto E, vértice do triângulo ABE. Qual é a altura
desse triângulo?
ESCALENO
R: 80cm
S=
b ⋅h
2
ISÓSCELES
S=
143) A sombra de uma pessoa que tem 1,80m de
b⋅h
2
altura mede 60cm. No mesmo momento, a seu lado, a
sombra projetada de um poste mede 2,00m. A altura
do poste mede:
R: 6m
144) Para estimar a profundidade de um poço, que
RETÂNGULO
tem 1,20m de diâmetro, um bombeiro cujos olhos
estão a 1,80m de altura posiciona-se a 0,30m de sua
borda. Dessa forma, a borda do poço esconde
exatamente seu fundo, como mostra a figura abaixo.
Com estes dados, o bombeiro conclui que o poço tem
a profundidade de:
R: 7,20m
Pitágoras → a 2 = b 2 + c 2
S=
a ⋅h b ⋅c
=
2
2
146) A hipotenusa de um triângulo retângulo mede 10
cm e o perímetro mede 24 cm. A área do triângulo é:
R: 24cm²
145)Uma pessoa caminha sobre uma rampa inclinada
(inclinação constante) de 3,5m de altura. Após
caminhar 12m sobre ela, se encontra a 1,5m de altura
em relação ao solo. Para atingir o ponto mais alto da
rampa, quantos metros esta pessoa deve ainda
caminhar?
R: 16m
147) Se um viajante percorre em seqüência 10km na
direção Oeste, 3km na direção Norte, 5km na direção
Oeste e 11km na direção Sul, a distância entre os
pontos de partida e de chegada, é igual a:
R: 17km
18
2009
Neste curso os melhores alunos estão sendo preparados pelos melhores Professores
MATEMÁTICA
SATVIRTUA
148) Uma escada com 10m de comprimento foi
PROF PEDRÃO
LOSANGO
apoiada em uma parede que é perpendicular ao solo.
Sabendo-se que o pé da escada está afastada 6m da
S=
base da parede, determine a altura em metros,
D⋅d
2
alcançada pela escada.
R: 8m
149) Na venda de uma chácara com formato e
TRAPÉZIOS
dimensões dados na figura abaixo, o corretor recebeu
uma comissão de cinco por cento sobre o preço de
ESCALENO
venda. Como o preço de venda do metro quadrado foi
de 12 reais, o corretor recebeu de comissão
S=
(B + b ) ⋅ h
R: R$10095,00
2
RETÂNGULO
(
h
b2
B
S
=
+
)⋅
150) Calcule em metros quadrados, a área limitada
pela figura plana.
ISÓSCELES
R: 18m²
4m
S=
(B + b) ⋅ h
2,5m
2
PARALELOGRAMOS
3m
SIMPLES
2m
S = b ⋅h
2m
151) O número de ladrilhos de 20cm por 30cm, cada
RETÂNGULO
um, necessários para ladrilhar um banheiro de 5,94m2
S = b ⋅h
2009
de área é:R: 99
Neste curso os melhores alunos estão sendo preparados pelos melhores Professores
19
MATEMÁTICA
SATVIRTUA
PROF PEDRÃO
152) Queremos revestir uma parede (figura abaixo),
A dificuldade, porém, está em evitar que o bloqueio
usando azulejos de 20cm x 20cm. Já dispondo de 342
extrapole
peças desse azulejo, a quantidade exata de peças a
determinado presídio inteiramente contido em um
serem compradas é:
círculo com raio de 500 m, no qual a antena para o
R: 73
bloqueio esteja instalada no centro deste círculo e o
a
área
do
presídio.
Supondo
um
bloqueio de celulares extrapole este círculo em 10%
do raio, que corresponde à área indevidamente
bloqueada fora deste círculo:
R: 52500 π m²
154) Na figura, a seguir, a área hachurada é de 16 π
2
cm . Sabendo-se que a diferença entre os dois raios é
CIRCUNFERÊNCIA E CÍRCULO
2cm, determine o valor numérico do produto desses
raios.
R: 15
155) Um retângulo está inscrito num círculo de 5 cm
de raio, e o perímetro do retângulo é de 28 cm.
Calcular, em centímetros quadrados, a área do
retângulo.
R: 48 cm²
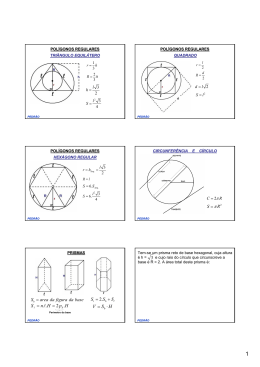
POLÍGONOS REGULARES
C = 2πR
S = πR 2
TRIÂNGULO EQUILÁTERO
153) Com a crise nas penitenciárias brasileiras
decorrentes das rebeliões simultâneas em várias
instituições, houve discussões sobre o uso de
bloqueadores de celulares. "O princípio do bloqueio é
gerar um sinal, por meio de uma antena instalada
internamente no presídio, que interfere na freqüência
da rede celular e que seja mais forte do que o sinal da
operadora".
Fonte: Eduardo Neger em entrevista publicada por
r=
1
h
3
h=
l 3
2
IDG NOW! www.idgnow.com.br em 16/05/06. Acesso
em 20/07/2006.
20
2009
R=
2
h
3
S=
l2 3
4
Neste curso os melhores alunos estão sendo preparados pelos melhores Professores
MATEMÁTICA
SATVIRTUA
PROF PEDRÃO
QUADRADO
157) Considere que a figura abaixo ilustra um triângulo
eqüilátero inscrito em uma circunferência de raio igual
a 12cm. Nessa situação, a área do triângulo inscrito,
vale:
R: 108 3 cm²
r=
l
2
R=
d
2
S = l2
d=l 2
158) Certa cerâmica é vendida em caixas fechadas
com 40 unidades cada. As peças são quadrados de
HEXÁGONO REGULAR
30 cm de lado. Sabendo-se que há uma perda de
10%, devido à quebra no assentamento, e que o preço
da caixa é R$ 36,00, o valor gasto somente com esse
2
material para revestir 240 m de piso é:
R: R$2666,60
159) Um quadrado de lado 8cm foi dividido conforme
mostra a figura. A área em branco dessa figura mede:
R: 32cm²
r = h ∆eq =
l 3
2
S = 6.S ∆eq = 6 ⋅
R=l
l2 3
4
156) Considere a circunferência inscrita em um
triângulo eqüilátero de lado igual a 12cm, conforme
mostrado na figura ao lado. Nesse caso, a área da
circunferência é igual a:
R: 12 π cm²
160) Um triângulo eqüilátero tem o mesmo perímetro
que um hexágono regular cujo lado mede 1,5 cm.
Calcule:
a) O comprimento de cada lado do triângulo.
b) A razão entre os lados do hexágono e do triângulo.
R: a)3
2009
b)1/2
Neste curso os melhores alunos estão sendo preparados pelos melhores Professores
21
MATEMÁTICA
SATVIRTUA
161) Dois lados opostos de um quadrado têm um
PROF PEDRÃO
HEXAEDRO REGULAR OU CUBO
aumento de 30% e os outros dois lados opostos têm
um decréscimo de 30%. Nestas condições a área da
figura: R: reduziu em 9%
GEOMETRIA ESPACIAL
PRISMAS
d=a 2
D=a 3
S t = 6a 2
V = a3
S b = área da figura base
162) A caixa de água de um certo prédio possui o
S l = n ⋅ l ⋅ H = 2pb ⋅ H,
onde 2p b = perímetro da
base
S t = 2S b + S l
formato de um prisma reto de base quadrada com 1,6
m de altura e aresta da base medindo 2,5 m. Quantos
litros de água há nessa caixa no instante em que 3/5
V = Sb ⋅ H
de sua capacidade estão ocupados?
PRISMAS NOTÁVEIS
PARALELEPÍPEDO RETÂNGULO
R: 6000litros
163) Uma caixa d’água está vazia e será abastecida
por uma torneira de vazão constante de 8 litros por
minuto. Sabendo que o formato interno dessa caixa é
o de um paralelepípedo reto com base retangular de
medidas 110 cm por 250 cm, calcule o tempo
necessário para que a caixa contenha água até a
altura de 80 cm.
R: 4h35min
164) Uma confeitaria derreteu uma barra de chocolate
de 30cm de comprimento por 10cm de largura e 2cm
2
2
2
2
2
2
d = a +b
de altura e moldou tabletes de 0,5cm de altura por
2
2
D = d +c = a +b +c
S t = 2ab + 2ac + 2bc
V = abc
2
3cm de largura e 8cm de comprimento, conforme
mostra a figura. Supondo que não ocorram perdas de
chocolate, o número de tabletes que puderam ser
feitos foi:
R: 50
22
2009
Neste curso os melhores alunos estão sendo preparados pelos melhores Professores
MATEMÁTICA
SATVIRTUA
PROF PEDRÃO
170) Considerando que uma das dimensões de um
paralelepípedo retângulo mede 6dm, e as demais
dimensões
são
diretamente
proporcionais
aos
números 8 e 2, e que a soma de todas as arestas é
44dm,
calcule,
165) Para minimizar-se um problema de poluição
paralelepípedo.
ambiental, houve necessidade de se construir um
R: 68dm²
em
dm2,
a
área
total
desse
tanque com forma de paralelepípedo de faces
retangulares, com 40m de comprimento, 30m de
171) O volume de um paralelepípedo retângulo é
largura e 20m de altura. Inicialmente, colocou-se água
24m .
até
proporcionais aos números 4, 3 e 2, calcule, em
2/3
de
sua
capacidade
e,
em
seguida,
depositaram-se os dejetos. Foram então ocupados
3
3
19600m . o volume dos dejetos, em m , é:
3
Sabendo-se
que
suas
dimensões
são
metros quadrados, a área total desse paralelepípedo.
R: 52m²
R: 3600m³
172) Usando um pedaço retangular de papelão, de
166)Um aquário em forma de paralelepípedo reto, de
dimensões 12cm e 16cm, desejo construir uma caixa
altura 40 cm e base retangular horizontal com lados
sem tampa, cortando, em seus cantos, quadrados
medindo 70 cm e 50 cm, contém água até um certo
iguais de 2cm de lado e dobrando, convenientemente,
nível. Após a imersão de um objeto decorativo nesse
a parte restante. A terça parte do volume da caixa, em
aquário, o nível da água subiu 0,4 cm sem que a água
cm , é:
entornasse. Então o volume do objeto imerso é:
R: 64cm³
3
R: 1,4litros
173) Um tanque, em forma de paralelepípedo, tem por
167) Admita que, ao congelar-se, a água aumenta em
base um retângulo de lados 0,50m e 1,20m. Uma
1
o seu volume. O volume de água a congelar para
15
pedra, ao afundar completamente no tanque, faz o
obter-se um bloco de gelo de
10 cm × 5cm × 6 cm, em m l , é de:
nível da água subir 0,01m. Então, o volume da pedra,
em decímetros cúbicos, é:
R: 6dm³
R: 281,25ml
174) A área total de um paralelepípedo reto retângulo
168) Uma caixa d’água, em forma de paralelepípedo
é de 376 m e as suas dimensões são proporcionais
retângulo, de dimensão 6,5m; 3m e 1,5m tem
aos números 3, 4 e 5. Determine a décima parte do
capacidade de (resposta em litros):
volume desse paralelepípedo.
R:
R: 48m³
2
169) Ao empilhar tijolos medindo 20cm x 10cm x 5cm,
sem deixar espaços vazios entre eles e sem quebrálos, formou-se um cubo de 1m de lado. A pilha tem
quantos tijolos?
R: 1000
2009
Neste curso os melhores alunos estão sendo preparados pelos melhores Professores
23
MATEMÁTICA
SATVIRTUA
CILINDRO
PROF PEDRÃO
178)Um cilindro circular reto de volume 108π cm3 tem
altura igual ao quádruplo do raio da base. Esse raio,
em centímetros, mede:R: 3cm
179) Considere uma lata cilíndrica de raio r e altura h,
cujo volume é dado por V =
π r2h, completamente
cheia de um determinado suco. Esse suco deve ser
distribuído totalmente em copos também cilíndricos,
cuja altura é um quarto da altura da lata e cujo raio é
S b = área da figura da base = πR 2
S l = 2p b ⋅ H = 2πRH
dois terços do raio da lata. Portanto, o número de
copos necessários para encher totalmente os copos,
será de:
S t = 2S b + S l
R: 9 copos
V = Sb ⋅ H
OBS.: CILINDRO EQUILÁTERO
180) Uma empresa usa, para um determinado
produto,
as
embalagens
fechadas
da
figura,
confeccionadas com o mesmo material, que custa R$
2
0,10 o cm . Supondo
π = 3 , a diferença entre os
custos das embalagens A e B é de: R: R$8,00
175) A área lateral de um cilindro eqüilátero é de
2
3
36 π m . O valor,em m , de
1
do volume desse
π
cilindro é:
R: 54m³
176) Uma caixa d’água tem forma cilíndrica com 10m
de altura e raio da base igual a 4m. Uma outra caixa
ESFERA
d’água será construída, baseada nesses valores,
aumentando 25% na altura e diminuindo 40% no raio.
De quantos metros cúbicos variará o seu volume?
R: 88 π m³
177) Se um cilindro eqüilátero mede 12m de altura,
3
então o seu volume, em m , vale:
R: 432 π m³
R 2 = r 2 + d2
S = 4 πR 2
V=
24
2009
4
πR 3
3
Neste curso os melhores alunos estão sendo preparados pelos melhores Professores
MATEMÁTICA
SATVIRTUA
181) Uma superfície esférica, de raio 13cm, é cortada
por um plano situado a uma distância de 12cm do
centro da superfície esférica, determinando uma
circunferência. O raio dessa circunferência, em cm, é:
PROF PEDRÃO
3
187) O volume, em cm , de um cubo circunscrito a
2
uma esfera de 16π cm de superfície é:
R: 64cm³
R: 5cm
LÓGICA DE INTERPRETAÇÃO
182) A área de um círculo máximo de uma esfera vale
81 π dm2. O volume dessa esfera é igual a:
01) Em um dia de trabalho no escritório, em relação
R: 972 π dm³
aos funcionários Ana, Cláudia, Luís, Paula e João,
183) Derretendo uma peça maciça de ouro de forma
esférica, quantas peças da mesma forma se pode
confeccionar com este ouro, se o raio das novas
peças é um terço do raio da anterior? Admita que não
houve perda de ouro durante o derretimento.
R: 27
sabe-se que:
-Ana chegou antes de Paula e Luís.
-Paula chegou antes de João.
-Cláudia chegou antes de Ana.
-João não foi o último a chegar.
Nesse dia, o terceiro a chegar no escritório para o
trabalho foi
184) Em uma caixa d’água cúbica vazia de lado 2m, é
colocada, cheia de água, uma esfera inscrita, com
espessura da parede desprezível. Estoura-se a esfera
e retiram-se seus resíduos. Qual a altura de água que
permanecerá dentro da caixa?
6
−π
3
R:
m
a) Ana.
b) Cláudia.
c) João.
d) Luís.
e) Paula.
02) Esta seqüência de palavras segue uma lógica:
-Pá
185) Ao mergulhar-se completamente uma esfera de
raio 30 cm em um tanque cilíndrico vertical de raio 40
cm, o nível da água no tanque eleva-se em h cm, sem
que ocorra transbordamento. Calcule h.
R: 22,5cm
-Japeri
Uma quarta palavra que daria continuidade lógica à
seqüência poderia ser
a) Casa.
b) Anseio.
186) Um recipiente de forma cilíndrica medindo 12cm
de raio interno é preenchido com água até uma altura
“h”. Uma bola ( esfera ) de raio 12cm é colocada no
fundo desse recipiente e constatamos que a água
recobre exatamente o nível da bola. Quanto mede a
altura “h”, ( em cm )?
-Xale
c) Urubu.
d) Café.
e) Sua.
03) A tabela indica os plantões de funcionários de uma
repartição pública em três sábados consecutivos:
R: 8cm
2009
Neste curso os melhores alunos estão sendo preparados pelos melhores Professores
25
MATEMÁTICA
SATVIRTUA
PROF PEDRÃO
Nas condições dadas, o valor numérico do símbolo
é:
a) 8
b) 6
c) 5
Dos seis funcionários indicados na tabela, 2 são da
d) 3
área administrativa e 4 da área de informática. Sabe-
e) 2
se que para cada plantão de sábado são convocados
2 funcionários da área de informática, 1 da área
05) Em uma repartição pública que funciona de 2ª a 6ª
administrativa, e que Fernanda é da área de
feira, 11 novos funcionários foram contratados. Em
informática. Um funcionário que necessariamente é da
relação aos contratados, é necessariamente verdade
área de informática é
que
a) Beatriz.
a) todos fazem aniversário em meses diferentes.
b) Cristina.
b) ao menos dois fazem aniversário no mesmo mês.
c) Julia.
c) ao menos dois começaram a trabalhar no mesmo
d) Ricardo.
dia do mês.
e) Silvia.
d) ao menos três começaram a trabalhar no mesmo
dia da semana.
04) A figura indica um quadrado de 3 linhas e 3
e) algum começou a trabalhar em uma 2 a feira.
colunas contendo três símbolos diferentes:
06) Comparando-se uma sigla de 3 letras com as
siglas MÊS, SIM, BOI, BOL e ASO, sabe-se que:
-MÊS não tem letras em comum com ela;
-SIM tem uma letra em comum com ela, mas que não
está na mesma posição;
-BOI tem uma única letra em comum com ela, que
está na mesma posição;
-BOL tem uma letra em comum com ela, que não está
na mesma posição;
-ASO tem uma letra em comum com ela, que está na
mesma posição.
Sabe-se que:
A sigla a que se refere o enunciado dessa questão é
-cada símbolo representa um número;
a) BIL
-a soma dos correspondentes números representados
b) ALI
na 1ª linha é 16;
c) LAS
-a soma dos correspondentes números representados
d) OLI
na 3ª coluna é 18;
e) ABI
-a soma de todos os correspondentes números no
quadrado é 39.
26
2009
Neste curso os melhores alunos estão sendo preparados pelos melhores Professores
MATEMÁTICA
SATVIRTUA
07) A tabela seguinte é a de uma operação .definida
a) (3,10)
sobre o conjunto E ={a,b,c,d,e}.
b) (1,8)
PROF PEDRÃO
c) (5,12)
d) (2,9)
e) (4,10)
10. Observe a figura seguinte:
Assim, por exemplo, temos: ( b ∆ d ) ∆ c = e ∆ c = b
Qual figura é igual à figura acima representada?
Nessas condições, se x ∈ E e d ∆ x = c ∆ ( b ∆ e ) ,
então x é igual a:
a) a
b) b
c) c
d) d
e) e
08) Uma pessoa distrai-se usando palitos para
construir
hexágonos
regulares,
na
seqüência
mostrada na figura abaixo.
11) Considere os conjuntos de números:
Se ela dispõe de uma caixa com 190 palitos e usar a
maior quantidade possível deles para construir os
hexágonos, quantos palitos restarão na caixa?
a) 2
b) 4
Mantendo para os números do terceiro conjunto a
c) 8
seqüência
d) 16
conjuntos anteriores para se obter o número abaixo do
e) 31
traço, é correto afirmar que o número x é
das
duas
operações
efetuadas
nos
a) 9
09) Considere os seguintes pares de números:
b) 16
(3,10) (1,8) (5,12) (2,9) (4,10)
c) 20
uma
d) 36
característica comum. O único par que não apresenta
e) 40
Observe
que
quatro
desses
pares
têm
tal característica é:
2009
Neste curso os melhores alunos estão sendo preparados pelos melhores Professores
27
MATEMÁTICA
SATVIRTUA
PROF PEDRÃO
12) Seis rapazes (Álvaro, Bruno, Carlos, Danilo, Elson
A partir dessas informações, pode-se concluir que
e Fábio) conheceram-se certo dia em um bar.
a) Evandro é consultor.
Considere as opiniões de cada um deles em relação
b) André é consultor.
aos demais membros do grupo:
c) Bruno é gerente.
d) Cecília é gerente.
• Álvaro gostou de todos os rapazes do grupo;
e) Débora é consultora.
• Bruno, não gostou de ninguém; entretanto, todos
gostaram dele;
15) Admitindo que certo Tribunal tem 1 800 processos
• Carlos gostou apenas de dois rapazes, sendo que
para serem lidos e que cada processo não possui
Danilo é um deles;
mais do que 200 páginas, é correto afirmar que
• Danilo gostou de três rapazes, excluindo-se Carlos e
a) não existem 2 processos com o mesmo número de
Fábio;
páginas.
• Elson e Fábio gostaram somente de um dos rapazes.
b) não existe processo com exatamente 9 páginas.
c) cada processo tem, em média, 9 páginas.
Nessas condições, quantos grupos de dois ou mais
d) existem pelo menos 9 processos com o mesmo
rapazes gostaram um dos outros?
número de páginas.
a) 1
e) mais de 100 000 páginas serão lidas na realização
b) 2
do serviço.
c) 3
d) 4
16) Quando somamos um número da tabuada do 4
e) 5
com um número da tabuada do 6, necessariamente
obtemos um número da tabuada do
13) Sabe-se que um número inteiro e positivo N é
a) 2
composto de três algarismos. Se o produto de N por 9
b) 6
termina à direita por 824, a soma dos algarismos de N
c) 8
é
d) 10
a) 11
e) 12
b) 13
c) 14
17) Observe atentamente a tabela:
d) 16
e) 18
14) Um departamento de uma empresa de consultoria
é composto por 2 gerentes e 3 consultores. Todo
cliente
desse
departamento
necessariamente
é
atendido por uma equipe formada por 1 gerente e 2
consultores. As equipes escaladas para atender três
diferentes clientes são mostradas abaixo:
Cliente 1: André, Bruno e Cecília.
Cliente 2: Cecília, Débora e Evandro.
De acordo com o padrão estabelecido, o espaço em
branco na última coluna da tabela deve ser preenchido
com o número
a) 2
b) 3
c) 4
d) 5
e) 6
Cliente 3: André, Bruno e Evandro.
28
2009
Neste curso os melhores alunos estão sendo preparados pelos melhores Professores
MATEMÁTICA
SATVIRTUA
PROF PEDRÃO
18) Para fazer pesagens, um comerciante dispõe de
uma balança de pratos, um peso de 1/2kg, um de 2kg
e um de 3kg.
A soma dos pontos que estão nas faces em contato
dos dois dados é
a) 7
b) 8
c) 9
d) 11
Com os instrumentos disponíveis, o comerciante
e) 12
conseguiu medir o peso de um pacote de açúcar. O
total de possibilidades diferentes para o peso desse
21) Em um trecho da letra da música Sampa, Caetano
pacote de açúcar é
Veloso se refere à cidade de São Paulo dizendo que
a) 6
ela é o avesso, do avesso, do avesso, do avesso.
b) 7
Admitindo que uma cidade represente algo bom, e que
c) 8
o seu avesso represente algo ruim, do ponto de vista
d) 9
lógico, o trecho da música de Caetano Veloso afirma
e) 10
que São Paulo é uma cidade:
a) equivalente a seu avesso.
19) O avesso de uma blusa preta é branco. O avesso
b) similar a seu avesso.
de uma calça preta é azul. O avesso de uma bermuda
c) ruim e boa.
preta é branco. O avesso do avesso das três peças de
d) ruim.
roupa é
e) boa.
a) branco e azul.
b) branco ou azul.
22) Sabe-se que:
c) branco.
I. Rita tem 6 anos a mais que Ana e 13 anos a mais
d) azul.
que Bia.
e) preto.
II. Paula tem 6 anos a mais que Bia.
Então, com relação às quatro pessoas citadas, é
20) Em um dado convencional os pontos que
correto dizer que:
correspondem aos números de 1 a 6 são colocados
a) Rita não é a mais velha.
nas faces de um cubo, de tal maneira que a soma dos
b) Ana é a mais nova.
pontos que ficam em cada par de faces opostas é
c) Paula é mais nova que Ana.
sempre igual a sete. Considere que a figura seguinte
d) Paula e Ana têm a mesma idade.
indica dois dados convencionais, e que suas faces em
e) Rita e Paula têm a mesma idade.
contato não possuem quantidades de pontos iguais.
2009
Neste curso os melhores alunos estão sendo preparados pelos melhores Professores
29
MATEMÁTICA
SATVIRTUA
PROF PEDRÃO
23) Com relação a três funcionários do Tribunal, sabe-
Considerando que na ordem alfabética usada são
se que:
excluídas as letras K, Y e W, a letra que substitui
I. João é mais alto que o recepcionista;
corretamente o ponto de interrogação é:
II. Mário é escrivão;
a) P
III. Luís não é o mais baixo dos três;
b) O
IV. um deles é escrivão, o outro recepcionista e o
c) N
outro segurança.
d) M
Sendo verdadeiras as quatro afirmações, é correto
e) L
dizer que:
a) João é mais baixo que Mário.
26) Suponha que, num banco de investimento, o
b) Luís é segurança.
grupo responsável pela venda de títulos é composto
c) Luís é o mais alto dos três.
de três elementos. Se, num determinado período,
d) João é o mais alto dos três.
cada um dos elementos do grupo vendeu 4 ou 7
e) Mário é mais alto que Luís.
títulos, o total de títulos vendidos pelo grupo é sempre
um número múltiplo de
24) Observe a figura a seguir e verifique que a faixa
a)) 3
é formada por três linhas de quadradinhos em que
b) 4
a primeira e terceira linhas são apenas por
c) 5
quadradinhos brancos. A segunda linha alterna
d) 6
quadradinhos brancos e pretos.
e) 7
27)
Três técnicos:
Amanda,
Beatriz e
Cássio
trabalham no banco – um deles no complexo
O número de quadradinhos brancos necessários
para uma faixa completa, de acordo com a figura,
computacional, outro na administração e outro na
segurança
do
Sistema
Financeiro,
não
respectivamente. A praça de lotação de cada um
mas contendo 60 quadradinhos pretos é:
deles é: São Paulo, Rio de Janeiro ou Porto Alegre.
a) 292
Sabe-se que:
b) 297
Cássio trabalha na segurança do Sistema Financeiro.
c) 300
O que está lotado em São Paulo trabalha na
d) 303
administração.
e) 480
Amanda não está lotada em Porto Alegre e não
trabalha na administração.
25) A figura a seguir apresenta algumas letras
É verdade que, quem está lotado em São Paulo e
disposta em triângulo, segundo determinado
quem trabalha no complexo computacional são,
critério.
respectivamente,
I
a) Cássio e Beatriz.
LJ
b) Beatriz e Cássio.
HGF
c) Cássio e Amanda.
? __ N __
d)) Beatriz e Amanda.
EDCBA
e) Amanda e Cássio.
30
2009
Neste curso os melhores alunos estão sendo preparados pelos melhores Professores
MATEMÁTICA
SATVIRTUA
PROF PEDRÃO
28) Na figura abaixo tem-se um conjunto de ruas
A figura que NÃO tem essa característica é a
paralelas às direções I e II indicadas.
a) I.
b) II.
c)) III.
d) IV.
e) V.
30) Considere a figura abaixo.
Sabe-se que 64 pessoas partem de P: metade delas
na direção I, a outra metade na direção II. Continuam
a caminhada e, em cada cruzamento, todos os que
chegam se dividem prosseguindo metade na direção I
e metade na direção II. O número de pessoas que
chegarão
nos
cruzamentos
A
e
B
são,
Supondo que as figuras apresentadas nas alternativas
respectivamente,
abaixo possam apenas ser deslizadas sobre o papel,
a) 15 e 20
aquela que coincidirá com a figura dada é:
b)) 6 e 20
c) 6 e 15
d) 1 e 15
e) 1 e 6
29) Das 5 figuras abaixo, 4 delas têm uma
característica geométrica em comum, enquanto uma
delas não tem essa característica.
2009
Neste curso os melhores alunos estão sendo preparados pelos melhores Professores
31
MATEMÁTICA
SATVIRTUA
PROF PEDRÃO
31) Um crime foi cometido por um e apenas uma
Pode-se garantir que a resposta correta é:
pessoa de um grupo de cinco suspeitos: Armando,
a) A
Celso, Edu, Juarez e Tarso. Perguntados sobre quem
b) B
era o culpado, cada um deles respondeu:
c) C
Armando: “Sou inocente”
d) D
Celso: “Edu é o culpado”
e) E
Edu: “Tarso é o culpado”
Juarez: “Armando disse a verdade”
34) Marta corre tanto quanto Rita e menos do que
Tarso: “Celso mentiu”
Juliana, Fátima corre tanto quanto Juliana. Logo:
Sabendo-se que apenas um dos suspeitos mentiu e
a) Fátima corre menos que Rita.
que todos os outros disseram a verdade, pode-se
b) Marta corre mais do que Juliana.
concluir que o culpado é:
c) Juliana corre menos do que Rita.
a) Armando
d) Fátima corre mais do que Marta.
b) Celso
e) Juliana corre menos do que Marta.
c) Edu
d) Juarez
35) Cinco times – Antares, Bilbao, Cascais, Deli e Elite
e) Tarso
– disputam um campeonato de basquete e, no
momento, ocupam as cinco primeiras posições na
32) Cinco ciclistas apostaram uma corrida.
classificação geral. Sabe-se que:
- Antares está em primeiro lugar e Bilbao está em
- “A” chegou depois de “B”.
quinto;
- “C” e “E” chegaram juntos.
- Cascais está na posição intermediária entre Antares
- “D” chegou antes de “B”
e Bilbao;
- Quem ganhou chegou sozinho.
- Deli está à frente do Bilbao, enquanto que o Elite
está imediatamente atrás do Cascais.
Quem ganhou a corrida
Nessas condições, é correto afirmar que:
a) A
a) Cascais está em segundo lugar.
b) B
b) Deli está em quarto lugar.
c) C
c)) Deli está em segundo lugar.
d) D
d) Elite está em segundo lugar.
e) E
e) Elite está em terceiro lugar.
33) Um teste de literatura, com cinco alternativas, em
36) Cátia é mais gorda do que Bruna. Vera é menos
que uma única é verdadeira, referindo-se à data do
gorda do que Bruna. Logo:
nascimento de um famoso escritor, apresenta as
a) Vera é mais gorda do que Bruna.
seguintes alternativas:
b) Cátia é menos gorda do que Bruna.
A.) Século XIX
c) Bruna é mais gorda do que Cátia.
B) século XX
d) Vera é menos gorda do que Cátia.
C) Antes de 1860
e) Bruna é menos gorda do que Vera.
D) depois de 1830
E) nenhuma das anteriores
32
2009
Neste curso os melhores alunos estão sendo preparados pelos melhores Professores
MATEMÁTICA
SATVIRTUA
37) Quatro meninas que formam uma fila estão
a) 0
usando blusas de cores diferentes, amarelo, verde,
b) 1
azul e preto. A menina que está imediatamente antes
c) 2
da menina que veste blusa azul é menor do que a que
d) 3
está imediatamente depois da menina de blusa azul. A
e) 4
PROF PEDRÃO
menina que está usando blusa verde é a menor de
todas e está depois da menina de blusa azul. A
40) Em um concurso, João, Pedro e Lígia tentam
menina de blusa amarela está depois da menina que
adivinhar um número selecionado entre os números
veste blusa preta. As cores das blusas da primeira e
naturais de 1 a 9. Ganha o concurso aquele que mais
da segunda menina da fila são, respectivamente:
se aproximar do número sorteado. Se João escolheu o
a) amarelo e verde
número 4, e Pedro o número 7, a melhor escolha que
b) azul e verde
Lígia pode fazer para maximizar sua chance de vitória
c) preto e azul
é o número:
d) verde e preto
a) 2
e) preto e amarelo
b) 3
c) 5
38) Hoje, o preço do quilograma de feijão é mais alto
d) 6
que o preço do quilograma de arroz. O dinheiro que
e) 8
Leo possui
não
é
suficiente para comprar 5
quilogramas de arroz. Baseando- se apenas nessas
41) Fábio, Antonio, Joaquim e Bernardo moram em
informações, pode-se concluir que o dinheiro de Leo:
casas separadas, todas localizadas no mesmo lado de
a) é suficiente para comprar 4 quilogramas de feijão.
uma rua retilínea. Sabe-se que a casa de Fábio
b) é suficiente para comprar 4 quilogramas de arroz.
localiza-se entre a casa de Joaquim e a casa de
c) não é suficiente para comprar 3 quilogramas de
Bernardo. Sabe-se também que a casa de Joaquim
feijão.
localiza-se entre a casa de Bernardo e a casa de
d) não é suficiente para comprar 2 quilogramas de
Antonio. Logo, a casa de:
arroz.
a) Fábio fica entre as casas de Antonio e de Joaquim.
e) não é suficiente para comprar 5 quilogramas de
b) Joaquim fica entre as casas de Fábio e de
feijão.
Bernardo.
c) Bernardo fica entre as casas de Joaquim e de
39) A respeito da resposta de um problema, Maurício,
Fábio.
Paulo, Eduardo e Carlos fizeram as seguintes
d) Antonio fica entre as casas de Bernardo e de Fábio.
afirmações:
e) Joaquim fica entre as casas de Antonio e de Fábio.
I) Maurício: É maior que 5.
42) Cada um dos três assessores administrativos de
II) Paulo: É menor que 10.
uma prefeitura (Paulo, Cristiano e Lucas) recebeu uma
III) Eduardo: É um número primo.
tarefa diferente. O prefeito solicitou um orçamento
IV) Carlos: É maior que 12.
para o novo dos três. Lucas recebeu a tarefa de
elaborar um parecer. Ao Paulo, que não é o mais
Entre as afirmações acima, quantas, no máximo,
velho, não foi solicitado que fizesse um orçamento. A
podem ser verdadeiras?
partir dessas informações, é correto afirmar:
2009
Neste curso os melhores alunos estão sendo preparados pelos melhores Professores
33
MATEMÁTICA
SATVIRTUA
PROF PEDRÃO
a) O prefeito solicitou um orçamento para Paulo.
- Juiz 1: “André foi o primeiro; Beto foi o segundo”
b) Lucas não é o mais velho.
- Juiz 2: “André foi o segundo; Dênis foi o terceiro”
c) Paulo é o mais novo.
- Juiz 3: “Caio foi o segundo; Dênis foi o quarto”
d) Cristiano recebeu do prefeito a solicitação de um
orçamento.
Sabendo que não houve empates, o primeiro, o
e) Cristiano é o mais velho.
segundo, o terceiro e o quarto colocados foram,
respectivamente,
43) Quatro carros, de cores amarela, verde, azul e
preta, estão em fila. Sabe-se que o carro que está
a) André,Caio, Beto, Dênis
imediatamente antes do carro azul é menor do que o
b) André,Caio, Dênis, Beto
que está imediatamente depois do carro azul; que o
c) Beto, André, Dênis, Caio
carro verde é o menor de todos; que o carro verde
d) Beto, André, Caio, Dênis
está depois do carro azul; e que o carro amarelo está
e) Caio, Beto, Dênis, André
depois do preto. O primeiro carro da fila:
a) é amarelo.
46) Luíza, Maria, Antônio e Júlio são irmãos. Dois deles têm
b) é azul.
a mesma altura. Sabe-se que:
c) é preto.
- Luíza é maior que Antônio
d) é verde.
e) não pode ser determinado apenas com esses
dados.
- Maria é menor que Luíza
- Antônio é maior do que Júlio
- Júlio é menor do que Maria.
44) Considere a seguinte afirmação: Todos os irmãos
Quais deles têm a mesma altura?
de André têm mais de 180cm de altura. Dessa
a) Maria e Júlio
afirmação, pode-se concluir que:
b) Júlio e Luíza
a) se Bernardo é irmão de André, então a altura de
c) Antônio e Luíza
Bernardo é menor que 180 cm.
d) Antônio e Júlio
b) se a altura de Caetano é maior que 180 cm, então
e) Antônio e Maria
ele é irmão de André.
c) se a altura de Dario é menor que 180 cm, então ele
47) Um feirante vende batatas e, para pesar, utiliza uma
balança de dois pratos, um peso de 1 kg, um peso de 3 kg e
não é irmão de André.
d) a altura de André é maior que 180 cm.
e) a altura de André é menor que 180 cm.
um peso de 10 kg. Considere a seguinte afirmação: “Este
feirante consegue pesar (com uma pesagem) n quilogramas
de batatas”. Quantos valores positivos de n tornam essa
afirmação verdadeira, supondo que ele pode colocar pesos
45) Quatro amigos, André, Beto, Caio e Dênis,
nos dois pratos?
obtiveram os quatro primeiros lugares em um
a) 7
concurso de oratória julgado por uma comissão de
b) 10
três juízes. Ao comunicarem a classificação final, cada
c) 12
juiz anunciou duas colocações, sendo uma delas
d) 13
verdadeira e a outra falsa:
34
2009
e) 14
Neste curso os melhores alunos estão sendo preparados pelos melhores Professores
MATEMÁTICA
SATVIRTUA
48) Um armazém recebe sacos de açúcar de 24 kg
para
que
menores.
sejam
O
empacotados em
único
instrumento
PROF PEDRÃO
a)
embalagens
disponível
para
pesagem é uma balança de dois pratos, sem os pesos
metálicos. Realizando uma única pesagem, é possível
b)
montar pacotes de:
a) 3 kg
b) 4 kg
c)
c) 6 kg
d) 8 kg
e) 12 kg
49) No retângulo abaixo, cada um dos quatro símbolos
d)
diferentes representa um número natural. Os números
indicados
fora
do
retângulo
representam
as
respectivas somas dos símbolos na linha 2 e nas
colunas 2 e 4:
e)
51) Um dado é feito com pontos colocados nas faces
Conclui-se
das informações que
o
símbolo
X
representa o número:
de um cubo, em correspondência com os números de
1 a 6, de tal maneira que a somados pontos que ficam
em cada par de faces opostas é sempre sete. Dentre
a) 3
as três planificações indicadas, a(s) única(s) que
b) 5
permite(m) formar, apenas com dobras, um dado com
c) 7
as características descritas é (são):
d) 8
e) 9
50) O desenho seguinte mostra a planificação de um
cubo que apresenta um número pintado em cada face,
como é mostrado na figura que segue.
A partir dessa planificação, qual dos seguintes cubos
pode ser montado?
2009
Neste curso os melhores alunos estão sendo preparados pelos melhores Professores
35
MATEMÁTICA
SATVIRTUA
a) I
PROF PEDRÃO
a)
b) I e lI.
c) I e III.
d) II e III.
e) I, II, III
52) Na figura, as faces em contato de dois dados
b)
possuem o mesmo número.
c)
Se a soma dos números nas faces opostas de cada
dado é sempre igual a 7, a maior soma possível dos
d)
números nas três faces sombreadas
da figura é:
a) 6
b) 8
c) 10
e)
d) 11
e) 15
53) A figura abaixo foi desenhada em cartolina e
dobrada de modo a formar um cubo.
54) Para montar um cubo, Guilherme recortou um
pedaço de cartolina branca e pintou de cinza algumas
partes, como na figura ao lado. Qual das figuras
abaixo representa o cubo construído por Guilherme?
Qual das alternativas mostra o cubo assim formado?
36
2009
Neste curso os melhores alunos estão sendo preparados pelos melhores Professores
MATEMÁTICA
SATVIRTUA
a)
PROF PEDRÃO
pega algumas blusas. O número mínimo de blusas
que Ana deve pegar para ter certeza de ter pegado ao
menos duas blusas da mesma cor é:
a) 6.
b)
b) 4.
c) 2.
d) 8.
e) 10.
c)
57) Numa caixa havia várias bolas, sendo 5 azuis, 4
amarelas, 3 vermelhas, 2 brancas e 1 preta. Renato
retirou 3 bolas da caixa. Sabendo que nenhuma delas
d)
era azul, nem amarela, nem preta, podemos afirmar a
respeito dessas 3 bolas que:
a) são da mesma cor.
e)
b) são vermelhas.
c) uma é vermelha e duas são brancas.
d) uma é branca e duas são vermelhas.
e) pelo menos uma é vermelha.
55) As doze faces de dois cubos foram marcadas com
números de 1 a 12, de modo que a soma dos números
de duas faces opostas em qualquer um dos cubos é
sempre a mesma. Joãozinho colou duas faces com
números pares, obtendo a figura ao lado. Qual o
produto dos números das faces coladas?
58) Numa gaveta há 6 meias pretas e 6 meias
brancas. Qual é o número mínimo de meias a se
retirar (no escuro) para garantir que: As meias
retiradas contenham um par da mesma cor?
a) 5
b) 6
c) 2
d) 3
e) 7
59) Numa gaveta há 6 meias pretas e 6 meias
a) 42
brancas. Qual é o número mínimo de meias a se
b) 48
retirar (no escuro) para garantir que: As meias
c) 60
retiradas contenham um par de cor branca?
d) 70
a) 8
e) 72
b) 6
56) Ana guarda suas blusas em uma única gaveta em
seu quarto. Nela encontram-se sete blusas azuis,
nove amarelas, uma preta, três verdes e três
c) 5
d) 4
e) 7
vermelhas. Uma noite, no escuro, Ana abre a gaveta e
2009
Neste curso os melhores alunos estão sendo preparados pelos melhores Professores
37
MATEMÁTICA
SATVIRTUA
PROF PEDRÃO
60) Para fazer 12 bolinhos, preciso exatamente de
64) Atente para os vocábulos que formam a sucessão
100g de açúcar, 50g de manteiga, meio litro de leite e
lógica, escolhendo a alternativa que substitui “X”
400g de farinha. A maior quantidade desses bolinhos
corretamente: LEIS, TEATRO, POIS, “X”.
que serei capaz de fazer com 500g de açúcar, 300g
a) Camarão.
de manteiga, 4 litros de leite e 5 quilogramas de
b) Casa.
farinha é:
c) Homero.
a) 48
d) Zeugma.
b) 60
e) Eclipse.
c) 72
d) 54
65) Uma propriedade lógica define a sucessão das
e) 42
seguintes cidades sergipanas: JAPARATUBA,
ITAPORANGA,
LAGARTO,
CARMÓPOLIS,
X.
61) A prefeitura de uma certa cidade fez uma
Escolha a alternativa que substitui X dentro da lógica
campanha que permite trocar 4 garrafas de 1 litro
do problema:
vazias por uma garrafa de 1 litro cheia de leite. Até
a) ARAUÁ
quantos litros de leite pode obter uma pessoa que
b) ESTÂNCIA
possua 43 dessas garrafas vazias?
c) BOQUIM
a) 11
d) ITABAIANA
b) 12
e) CRISTINÁPOLIS
c) 13
d) 14
66) São dados três grupos de 4 letras cada um:
e) 15
(MNAB) : (MODC) : (EFRS) : Se a ordem alfabética
adotada exclui as letras K,W e Y, então o grupo de
62) Um tijolo pesa um quilo mais meio tijolo. Quanto
quatro letras que deve ser colocado à direita do
pesa um tijolo e meio?
terceiro grupo e que preserva a relação que o
a) 1kg
segundo tem com o primeiro é:
b) 2kg
a) (EHUV)
c) 3kg
b) (EGUT)
d) 1,5kg
c) (EGVU)
e) 2,5kg
d) (EHUT)
e) (EHVU)
63) Atente para os vocábulos que formam a sucessão
lógica:
HOMERO,
DEPOIS,
TEATRO,
DEVEIS,
67) Tem-se abaixo o algoritmo da multiplicação de
COITO,.............. Determine a alternativa que preenche
dois números inteiros, no qual alguns algarismos
logicamente a lacuna:
foram substituídos pelas letras X, Y, Z e T.
a) PÉS
b) MÃO
c) COSTAS
d) BRAÇO
e) TRONCO
Para que o resultado esteja correto, os algarismos
X, Y, Z e T devem ser tais que
38
2009
Neste curso os melhores alunos estão sendo preparados pelos melhores Professores
MATEMÁTICA
SATVIRTUA
PROF PEDRÃO
a) X + 3T = Y + Z
69) Observe que as figuras abaixo foram dispostas,
b) X + 2Y = 3T + Z
linha a linha, segundo um determinado padrão.
c) Y + 3T = X + Z
d) Y + 2T = 2X – Z
e) Z + 2Y = 3X – Z
68) Em cada linha do quadro abaixo, as figuras foram
desenhadas obedecendo um mesmo padrão de
construção:
Segundo o padrão estabelecido, a figura que substitui
corretamente o ponto de interrogação é:
a)
a)
b)
b)
c)
c)
d)
d)
e)
e)
2009
Neste curso os melhores alunos estão sendo preparados pelos melhores Professores
39
MATEMÁTICA
SATVIRTUA
PROF PEDRÃO
70)
Então o produto entre o valor de uma bola, um
triângulo e um quadrado, é:
a) 160
b) 135
c) 120
d) 108
e) 100
GABARITO – LÓGICA DE INTERPRETAÇÃO
01) e
02) b
03) a
04) e
05) d
06) b
07) e
08) b
09) e
10) d
11) b
12) a
13) c
14) a
15) d
16) a
17) b
18) e
21) e
22) c
23) b
24) d
25) a
26) a
27) d
28) b
29) c
30) d
31) e
32) d
33) e
34) d
35) c
36) d
37) c
38) e
41) e
42) d
43) c
44) c
45) b
46) e
47) d
48) e
49) a
50) b
51) d
52) e
53) b
54) c
55) c
56) a
57) e
61) d
62) b
63) a
66) b
67) a
68) b
40
2009
58) d
19) e
39) d
59) a
64) c
69) c
20) a
40) b
60) e
65) c
70) b
Neste curso os melhores alunos estão sendo preparados pelos melhores Professores