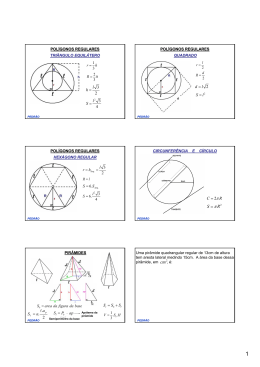
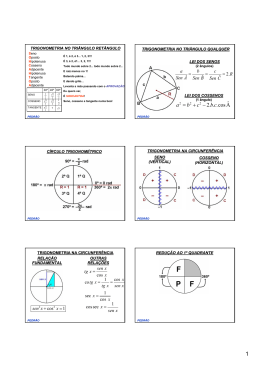
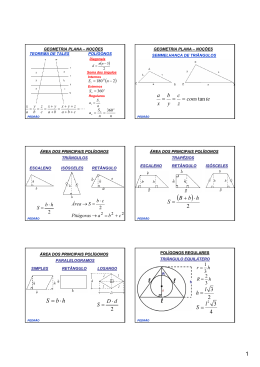
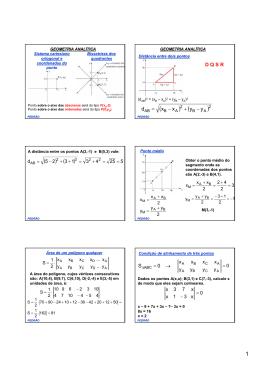
POLÍGONOS REGULARES
POLÍGONOS REGULARES
TRIÂNGULO EQUILÁTERO
QUADRADO
l
2
d
R=
2
1
r= h
3
2
R= h
3
h=
S=
r=
d =l 2
l 3
2
l
2
S = l2
3
4
PEDRÃO
PEDRÃO
POLÍGONOS REGULARES
CIRCUNFERÊNCIA
E
CÍRCULO
HEXÁGONO REGULAR
r = h∆eq. =
l 3
2
R=l
S = 6.S ∆eq.
S = 6.
l2 3
4
C = 2π R
S = π R2
PEDRÃO
PEDRÃO
PRISMAS
Sb = area da figura da base
S l = n.l.H = 2 pb .H
Tem-se um prisma reto de base hexagonal, cuja altura
é h = 3 e cujo raio do círculo que circunscreve a
base é R = 2. A área total deste prisma é:
St = 2.Sb + Sl
V = Sb ⋅ H
Perímetro da base
PEDRÃO
PEDRÃO
1
Qual é o volume, em metros cúbicos, de um prisma
triangular reto em que a altura é igual a 10 3 metros e
a base, que é um triângulo eqüilátero, está inscrita em
uma circunferência de perímetro igual a 4π metros?
PRISMAS NOTÁVEIS
PARALELEPÍPEDO
RETÂNGULO OU ORTOEDRO
d 2 = a2 + b2
D = d 2 + c2 = a 2 + b2 + c2
2
St = 2.a.b + 2.a.c + 2.b.c
V = a.b.c
PEDRÃO
HEXAEDRO
REGULAR OU CUBO
d = a. 2
D = a. 3
St = 6.a 2
V = a3
PEDRÃO
Um aquário em forma de paralelepípedo reto, de altura
40 cm e base retangular horizontal com lados medindo
70 cm e 50 cm, contém água até um certo nível. Após a
imersão de um objeto decorativo nesse aquário, o nível
da água subiu 0,4 cm sem que a água entornasse.
Então o volume do objeto imerso é:
Admita que, ao congelar-se, a água aumenta em 1/15 o
seu volume. O volume de água a congelar para obter-se
um bloco de gelo de 10 cm×5cm×6 cm, em ml , é de:
1m 3 = 1000l
LEMBRE-SE:
1dm 3 = 1l
1cm 3 = 0,001l = 1ml
PEDRÃO
Na figura abaixo, que representa um cubo, o perímetro
do quadrilátero ABCD mede 8(1 + 2 )cm. Calcule o
volume do cubo em centímetros cúbicos.
B
PEDRÃO
Um engenheiro deseja projetar um bloco vazado cujo orifício sirva
para encaixar um pilar. O bloco, por motivos estruturais, deve ter
a forma de um cubo de lado igual a 80cm e o orifício deve ter a
forma de um prisma reto de base quadrada e altura igual a 80cm,
conforme as figuras seguintes. É exigido que o volume do bloco
deva ser igual ao volume do orifício. É correto afirmar que o valor
“L” do lado da base quadrada do prisma reto corresponde a:
A
C
D
PEDRÃO
PEDRÃO
2
PRISMAS
CILINDRO
Sb = area da figura da base
Sl = 2.Pb ⋅ H
Sl = 2.π .R.H
Perímetro da base
OBS.: CILINDRO EQUILÁTERO
St = 2.Sb + Sl
V = Sb ⋅ H
PEDRÃO
PEDRÃO
Uma caixa d’água tem forma cilíndrica com 10m de
altura e raio da base igual a 4m. Uma outra caixa
d’água será construída, baseada nesses valores,
aumentando 25% na altura e diminuindo 40% no raio.
De quantos metros cúbicos variará o seu volume?
Se um cilindro eqüilátero mede 12m de altura, então o
seu volume, em m3, vale:
PEDRÃO
PEDRÃO
3