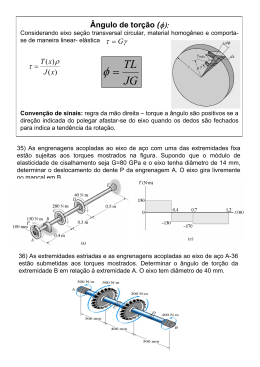
7. Torção, tensão de corte e ângulo de rotação
Terminologia:
T
T
Relativamente à deformação
Torção livre: o empeno da secção transversal não está constrangido
(empeno = deformação na direcção do eixo da peça)
Relativamente aos outros esforços
Torção pura: o momento torsor T é constante ao longo do eixo do elemento
e forma o único esforço interno
Estruturas onde o único esforço interno é o momento torsor:
sistemas rectilíneos de eixo comum sujeitos à carga do momento torsor
Torção pura e livre nas peças prismáticas
Teoria de Saint-Vénant :
O empeno ocorre e é igual em todas as secções transversais
Veio: peça linear, simetria radial da secção transversal, sujeita à torção
não exibe empeno, ou seja secções transversais mantém-se planas
Teoria de Coulomb
Teoria de Coulomb:
1. as secções transversais rodam nos seus planos como se fossem rígidos
(em torno do centro de corte, também chamado centro de torção,
que nas secções maciças coincide com o centróide)
2. o ângulo da rotação de cada secção, chamado o ângulo de torção β,
é proporcional à distância da secção à secção que se supôs fixa
3. as secções transversais mantém-se planas
Hipótese 2
β = xθ
y
ϕ
ϕ
C
Hipótese 3
u=0
τxs (r )
x
y
β = xθ
z
rxθ
z
Hipótese 1
w = rxθ cos ϕ = xyθ
v = − rxθ sin ϕ = − xzθ
γ xy = − zθ
γ xz = yθ
τ xy = −Gzθ
τ xz = Gyθ
τ xs = τ2xy + τ2xz = Gθ z 2 + y 2 = Gθr
na direcção de tangente às circunferências de mesma tensão
θ ângulo de torção por unidade de comprimento ou
taxa de variação do ângulo de torção na direcção do eixo do veio
Elementos
rectilíneos
mantém o seu
eixo recto
depois da
deformação
Equação de equivalência
T = ∫ (τ xz y − τ xy z )dA = Gθ ∫ (y 2 + z 2 )dA = GθI p
A
pode-se verificar que os outros
esforços são nulos
A
r
τxs (r ) =
R
τxs (r )
1
I p = πR 4
2
τ
max
xs
T
= R
Ip
T
r
Ip
T
θ=
GIp
R 2 R1
τxs (r )
T
max
1
4
4
τ
=
R2
I p = π(R 2 − R 1 ) xs
Ip
2
Ip: momento polar de inércia =Iy+Iz (invariante)
Na formula geral tem que se usar IT constante de rigidez torsional, momento
torsional de inércia, momento de inércia em torção, mas para as secções com
simetria radial IT=IP
assegura igual ângulo de torção para o mesmo
Rigidez em torção: GIT = GIp
carregamento
(Módulo de) Resistência em torção:
Ip
WT = Wp =
R
ou
Ip
R2
τmax
=
xs
T
WT
assegura igual tensão de corte
máxima para o mesmo carregamento
Δβ = βL − β0
Define-se a variação de ângulo de torção
T x
T
T
(x ) = const ⇒ βL = β0 + ∫x dx = β0 + L
θ(x ) =
GI p
GIp
GIp
L
Δβ =
0
T
L
GI p
Sinal unicamente definido como para T, não é preciso introduzir o referencial
É preciso introduzir o referencial
para determinar o sinal do ângulo
x
β
Sistemas rectilíneos de eixo comum estaticamente indeterminados
sujeitos à carga de momento torsor
Condição de compatibilidade:
soma de variações de ângulo de
torção tem que ser igual a zero