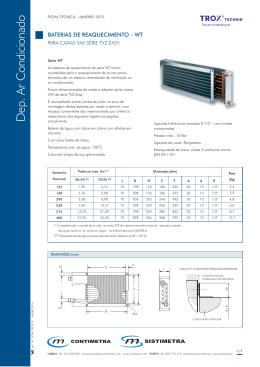
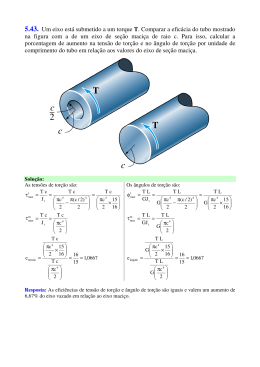
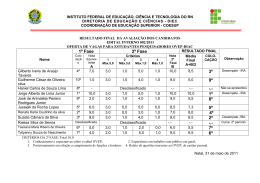
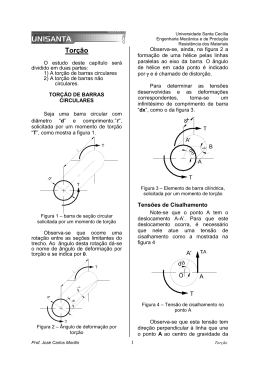
ENG 1007 – INTRODUÇÃO À MECÂNICA DOS SÓLIDOS
Segunda prova – turma B
24/04/2014
a
1 Questão (2,5 pontos)
O eixo conjugado ABCD está carregado como mostra a figura abaixo. Os diâmetros dos segmentos
AB, BC e CD são 60 mm, 40 mm e 20 mm, respectivamente. O módulo de elasticidade transversal é G
= 75 GPa. Pede-se:
a) a máxima tensão cisalhante em cada trecho;
b) o ângulo de rotação da seção D.
τ =
J =
Tr
J
π
2
( re4 − ri 4 )
φB − φ A =
TAB L AB
GJ
Resposta:
400 Nm × 16
= 9, 431MPa
π 0,063 m3
1600 Nm × 16
=
= 127,324MPa
π 0,043 m3
600 Nm × 16
=
= 381,972 MPa
π 0,023 m3
AB
a) τ máx
=
τ
BC
máx
CD
τ máx
b) ϕ AD =
600
−400
1600
32
 −400 × 0,5 1600 × 0,5 600 × 0,67 
+
+
= 0,381rad
9
75 × 10 π  0,064
0,044
0,024 
2a Questão (2,5 pontos)
As hélices de um navio estão acopladas a um eixo maciço, feito de aço (G = 84 GPa) e com 60 m de
comprimento, diâmetro externo de 340 mm e diâmetro interno de 260 mm. Para uma potência de saída
de 4,5 MW e rotação do motor igual a 20 rad/s, determinar
a) a tensão de cisalhamento máxima no eixo;
b) seu ângulo de torção.
T ( x ) Gρ
P = 2π nT ; τ ( x, ρ ) =
r( x )
2π ∫ G ρ 3d ρ
0
Resposta:
4,5MW
= 225kNm
20rad / s
225kNm × 0,17 m
a) τ máx =
= 44,306 MPa
π ( 0,17 4 − 0,134 ) m4 2
T=
b) ∆ϕ =
225kNm × 60m
= 0,186rad
84GPa × π ( 0,17 4 − 0,134 ) m 4 2
3a Questão (2,5 pontos)
O tubo de alumínio tem espessura de 5 mm e as dimensões da seção transversal externa mostradas.
Determinar:
a) a tensão de cisalhamento média máxima nele desenvolvida;
b) o ângulo máximo de torção do tubo, para um comprimento L = 5 m e o módulo de elasticidade G =
28 GPa.
T
τ=
2A m t
dϕ =
T ⌠ ds

dx
4A 2m G ⌡Cm t
Resposta:
a) τ máx =
280 Nm
= 2,033MPa
2(0,15 − 0,005)(0,1 − 0,005) × 0,005m3
b) ∆ϕ =
( 280 Nm × 2m − 145Nm × 3m ) × 2(0,15 − 0,005 + 0,1 − 0,005)m = 0,00449rad
4(0,15 − 0,005) 2 (0,1 − 0,005)2 × 0,005m5 × 28GPa
4a Questão (2,5 pontos)
Um eixo está submetido a um torque T. Comparar a eficácia do tubo mostrado na figura com a de um
eixo de seção maciça de raio c. Para isso, calcular, em relação aos valores do eixo de seção maciça, a
porcentagem de aumento
a) na tensão de torção;
b) no ângulo de torção por unidade de comprimento do tubo.
dφ
T(x )
=
r(x)
3
dx 2π
∫ Gρ dρ
0
τ=
T ( x) G ρ
2π ∫
r ( x)
0
Gρ 3dρ
Resposta:
maciço
a) τ máx
=
T
;
π c3 / 2
b) ∆ϕ maciço =
TL
π Gc 4 / 2
vazado
τ máx
=
;
T
16T
16 maciço
=
= τ máx
3
3
π ( c − c / 16 ) / 2 15π c / 2 15
∆ϕvazado =
3
TL
16TL
16
=
= ∆ϕmaciço
4
4
π
15
Gc
/
2
15
π G ( c − c / 16 ) / 2
4
vazado
O tubo de seção vazada é menos eficiente, já que tanto τ máx
quanto ∆ϕvazado são 16 15 ≈ 1,067 maiores
que no tubo de seção cheia. (Em compensação, a área do tubo vazado é apenas 3/4 da área do tubo de
seção cheia, o que dá uma maior eficiência para a mesma área transversal.)