EXPOENTE
3
2
=
8
RESULTADO
BASE
Podemos entender a potenciação como uma multiplicação de fatores iguais.
A Base será o fator que se repetirá
O expoente indica quantas vezes a base vai ser multiplicada por ela mesma.
25 = 2 . 2 . 2 . 2. 2 = 32
53 = 5 . 5 . 5 = 125
Definição:
an = a. a. a. a….a
n fatores
a
1
=
a
a0 = 1
an 
1
an
Propriedades:
I)
am .an  am n
m
II)
a
mn

a
an
a .b  a.b
m
III)
a
a
 
m
b
b
m
IV)
a   a
m n
v)
m
m
m
m.n
Exemplos:
1)
2³=2.2.2=8
2)
10¹ = 10
3)
10º = 1
6)
24 4  3 1
2 2 2
3
2
5)
7)
a .a  a
4
6
 22   2  4
 2     
3  3 9
2
1 1
2


2
4)
2 4
2
10
8)
2 
2 3
 26  64
23
9)
ALGUMAS ATIVIDADES
3
=
38 = 6561
Notação Científica
-São potências que servem para expressar grandes números, como
números muito pequenos.
A potência que expressa uma Notação Científica é composta de duas partes:
EXPOENTE
POSITIVO
OU NEGATIVO
N
x
10
Número entre 1 e 10
também
RAIZ
A Radiciação é a operação inversa da potenciação.
ÍNDICE
x
RADICAL
R    raiz
RADICANDO
x
r 
x
r
Exemplos
3
27  3
3
16  4
2
Importante:
Toda Radical sem índice indica que é uma Raiz Quadrada
Quadrados Perfeitos
São todos os números que possuem raiz quadrada exata.
1  1 e 1² = 1
4  2 e 2² = 4
4 porque
9  3 e 3² = 9
9 porque
16 porque 16  4 e 4² = 16
25  5 e 5² = 25
25 porque
36 porque 36  6 e 6² = 36
49  7 e 7² = 49
49 porque
64 porque 64  8 e 8² = 64
81 porque 81  9 e 9² = 81
100 porque 100  10 e 10² = 100
Raízes não Exatas
1 porque
a) Decompor o Radicando em fatores primos
b) Substituir o Radicando pela decomposição , expressa em potência.
c) Simplificar os expoentes com os índices.
Observação:As potências que forem simplificadas saem para fora do radical e as que não
forem permanecem dentro do radical.
Exemplo:
44 
2
2 .11
=
2
11
Decomponha
a)
20
b)
50
c)
160
MULTIPLICAÇÃO DE RAIZES DE MESMO INDICE
Para multiplicarmos raízes com o mesmo índice, mantemos o índice e multiplicamos os radicandos.
=
=
Exemplo :
DIVISÃO DE RAIZES DE MESMO INDICE
Para dividirmos raízes com o mesmo índice, mantemos o índice e dividimos os radicandos.
=
=
=
POTÊNCIA DE UMA RAIZ
)m =
Exemplo
)7 =
1) Represente as potências a seguir na forma de
multiplicação e calcule, conforme o exemplo:
106 = 10 x 10 x 10 x 10 x 10 x 10= 1 000 000
a)
b)
c)
d)
e)
2³___________________________
3²___________________________
45___________________________
7³___________________________
84___________________________
2)Encontre o valor de uma potência em que :
a) a base é 3 e o expoente é 4.
________________________________________
b)O expoente é sete e a base é 2.
________________________________________
3) Dois amigos, João e Marta, estavam brincando
com uma calculadora, quando Marta digitou as
seguintes operações:
2x2x2x2x2x2x2x2x2x2x2x2x2x2x2 =
E no visor apareceu o número 32 768. Os dois
amigos começaram então, o seguinte diálogo:
João: Se você repetiu a multiplicação 15 vezes
isto quer dizer que 32 768 é o resultado de 215,
não é?
Marta: Sim! E se multiplicarmos novamente por
2 iremos encontrar o resultado de 216.
João: Mas o que acontece se eu dividir 32 768 por
2?
Marta : Você vai chegar a 16 384.
João: Mas isso é o resultado de 2 elevado a
quanto?
Marta : Não sei...
Com base nesse diálogo responda:
a) Qual é o resultado de 216?
____________________________________
b) 2 elevado a que número resulta 16 384?
____________________________________
4) Uma colônia de bactérias duplica o número de
sua população a cada hora.
Se inicialmente temos 1000 bactérias nessa
colônia, responda:
a)Quantas bactérias existirão depois de 3 horas?
________________________________________
b)Depois de quantas horas o numero de bactérias
da colônia ultrapassará 1 milhão?
________________________________________
5)Considerando que 124 = 20 736 calcule:
a) 125__________________________
b)126___________________________
Calcule:
a)
b)
c)
d)
e)
f)
g)
h)
i)
j)
00_______________________
27_______________________
13²______________________
105______________________
11²______________________
35 _______________________
9³_______________________
100³_____________________
2017²____________________
23³______________________
6) Um e-mail foi enviado para cinco pessoas
no primeiro dia do mês. O conteúdo da
mensagem era uma brincadeira que fazia com
que toda pessoa que a recebesse encaminhasse o
e-mail para mais 5 pessoas no dia seguinte.
Considerando que todas as pessoas que
receberam o e-mail participaram da brincadeira,
enviando a mensagem para mais 5 pessoas no
dia seguinte e que ninguém recebeu o e-mail
duas vezes, responda:
a) Quantas pessoas receberam esse e-mail no
sexto dia desse mês?
______________________________________
b)Represente na forma de potência de base
cinco, o número de pessoas que receberam esse
e-mail no dia 30.
______________________________________
c)”Viral da internet” é um termo utilizado para se
referir a algum conteúdo que se espalhe de maneira
muito rápida pela rede mundial de computadores.
Por que você acha que esse nome é utilizado?
______________________________________
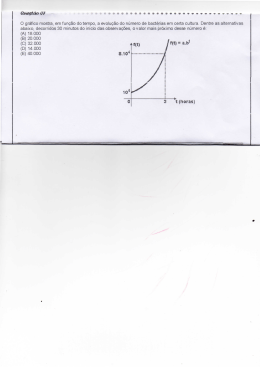
7)Em um recipiente foram colocadas, inicial- mente
duas bactérias. Observou-se que ao longo de 60
minutos elas duplicaram de quantidade a cada
minuto, ou seja , depois do primeiro minuto o
recipiente continha 4 bactérias, depois do segundo
minuto 8 e assim sucessivamente.
a) Represente, utilizando uma potência de base 2, a
quantidade de bactérias depois de passados 60 min.
______________________________________
b)Depois de quantos minutos as bactéria atingiram
metade do valor final?
______________________________________
8)Dado um conjunto A={2; 5; 7} podemos
formar um total de 7 conjuntos, cujos elementos
são unicamente elementos do conjunto A. Por
exemplo:
A1= {2}
A2= {5}
A3= {7}
A4= {2; 5}
A5= {2;7}
A6= {5;7}
A7={2;5;7}
Por meio da contagem, podemos deduzir que a
quantidade de conjuntos x que podemos formar,
utilizando unicamente os elementos de um
conjunto A qualquer é :
X = 2n -1
Em que n é a quantidade de elementos do
conjunto A. Encontre a quantidade de conjuntos
que podemos formar utilizando unicamente os
elementos de um conjunto que possua:
11)Os números inteiros que possuem raiz cúbica
exata são chamados de cubos perfeitos. Diga
quais dos números a seguir são cubos perfeitos.
a)
b)
c)
d)
e)
8_____________
49____________
64____________
121___________
125___________
12)Para calcularmos a área de um quadrado, basta
elevarmos a medida de seu lado ao quadrado; e se
quisemos encontrar a medida de seu lado, basta
extarirmos a raiz quadrado do valor de sua área.
Com base nessas informações, encontre o valor do
lado de cada um dos quadrados a seguir:
a)
Área 196 m²
__________________
a) 5 elementos
_______________________________________
b) 11 elementos
b)
_______________________________________
9)Para calcularmos o volume de um cubo, basta
elevarmos a medida de sua aresta ao cubo; e se
quisermos encontrar a medida da aresta, basta
extrair a raiz cúbica do valor de seu volume.
Com base nessa informação encontre o valor de
cada aresta do cubo cujo volume é 125 cm³.
Área 400 m²
__________________
Área 81 m²
_________________
c)
13)Calcule o resultado das raízes quadradas a
seguir, justificando-as conforme o exemplo:
_______________________________________
a)
_____________________________________
10)Os números inteiros que possuem raiz
quadrada exata São chamados de quadrados
perfeitos. Diga quais dos números a seguir são
quadros perfeitos.
b)
__________________________________
c)
__________________________________
d)
__________________________________
e)
__________________________________
a)
b)
c)
d)
e)
8_______________
49______________
64______________
121_____________
200_____________
14)Calcule as raízes a seguir. Se necessário, fatore os
radicandos antes de calcular.
a)
b)
c)
d)
e)
f)
g)
h)
i)
=_____________________________
=_____________________________
=_____________________________
=_____________________________
=____________________________
=____________________________
=_____________________________
=_________________________
=___________________________
15)Observe os calculos feitos por um aluno do 9º ano:
24 = 2 . 2. 2. 2 = 16
4² = 4 . 4 = 16
Ao refletir sobre os resultados, esse aluno concluiu que a
potenciação possui a propriedade comutativa.
Considerando essa situação e lembrando-se que uma
operação possuia propriedade comutativa quando a
ordem dos termos não altera o resultado, o aluno
cometeu algum erro em sua conclusão. Justifique sua
resposta.
19)Escreva as potências a seguir como uma
única potência de base 2.
a) (210)10___________________________
b) (45)4____________________________
c) (6411)11__________________________
d) (102410)5_________________________
e) [(8) 8]8___________________________
f) [(16 . 32)10]20______________________
g) [(2 . 4 . 8)³]10 . 512²_________________
h) (44)4_____________________________
i) (40968)7 __________________________
j) (16²)³ . (16²)³______________________
k) (1024³)10. (325)500 . (2048²)20.(44)5___
20)Lembrando que a potenciação possuia
propriedade distributiva em relação a divisão,
calcule:
21)Transforme as expressões de cada item em
uma potência com expoente negativo.
__________________________________________
__________________________________________
__________________________________________
a)
16)Simplifique as potências a seguir como uma única
potência.
a) (2 0075)7 _____________________
b) (2²)5 _________________________
c) (x9)5 _________________________
d) [(1111)11]11_____________________
e) {[(13²)4]3}10____________________
c)
17)Desenvolva e reduza as seguintes potências :
a) (7² . 4² )8 _____________________
b) (2³ . 24)2 _________________________
c) (2³ . 3²)0 _________________________
d) [(-1 )3 . (-4 )³]7_____________________
e) ( 55 . 66 . 77)²____________________
18)Reescreva a expressão a seguir em uma única
potência.(OMEP)
20
20
20
9 +9 +9
________________________________________
b)
d)0,001
e)0,0016
22) Para cada quilômetro, temos 10³ metros.
Para cada metro, temos 10³ milímetros. E para
cada milímetro, nós temos 10³ micrômetros.
Quantos micrômetros então, teremos em 1
quilômetro?
_______________________________________
23)Uma pessoa jovem tem em média 217 fios de
cabelo, enquanto uma pessoa com 50 anos de
idade possui em média 216 fios de cabelo. Qual
o percentual, em média, de cabelos de uma
pessoa com 50 anos em relação a uma pessoa
jovem?
______________________________________
Decomponha os radicais
1) 8
18) 75
2)
12
19) 76
3)
18
20) 80
4)
24
21) 84
5) 27
22) 90
6) 28
23) 99
7)
24) 120
32
8) 40
25) 125
44
26) 140
9)
10) 45
27) 150
11) 48
28) 160
12) 50
29) 162
13) 52
30) 180
14) 54
31) 196
15)
32) 200
63
16) 68
33) 256
17)
34) 484
72
RESPOSTAS
1) ) 2 2
2) 2 3
3)
3 2
4)
2 6
5) 3 3
6) 2 7
7)
4 2
8) 2 10
9)
2 11
10) 3 5
11) 4 3
12) 5
2
18) 5 5
19) 2 19
20) 4 5
21) 2
21
22) 3 10
23) 3
11
24) 2 30
25) 5 5
26) 2 35
27) 5 6
28) 4 10
29) 9
2
13) 2 13
30) 6 5
14) 3 6
31) 14
15) 3 7
16) 2 17
17) 6
2
32) 10
2
33) 16
34) 22