Escola Secundária de Santa Maria da Feira
Ficha de Avaliação de Matemática A
11º C Versão A
Fevereiro de 2009
I Parte
Escolha Múltipla
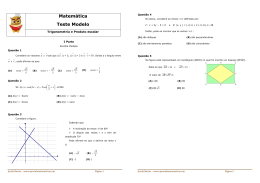
1- Na figura está a representação gráfica de uma função g .
1.1. A função g pode ser definida por :
(A)
( C)
2
x−2
1
g ( x ) = −1 −
x−2
g ( x ) = −1 +
x +1
x−2
(B)
g ( x) =
(D)
g ( x) = 2 +
1
x +1
1.2. As equações das assimptotas ao gráfico da função h, definida por :
h(x)= - 2 + g ( x + 1 )
são :
(A) x = 1 e y = -3
(B) x = 3 e y = -3
(C) x = 1 e y = 1
(D) x = 3 e y = 1
2- Na figura abaixo está representada uma circunferência de centro O e raio 1.
Os pontos A e B são extremos de um diâmetro da circunferência.
Considere que um ponto P, partindo de A, se desloca sobre o arco AB, terminando o seu percurso em B.
Para cada posição do ponto P, seja x a amplitude, em radianos, do ângulo AOP.
Seja f a função que, a cada valor de
x ∈ [0, π ] , faz corresponder o valor do
produto escalar OA ⋅ OP .
Qual dos gráficos seguintes pode ser o da função f?
(A)
(B)
(C)
(D)
3- Sabe-se que:
• o nível de álcool no sangue de uma pessoa , uma hora depois de ter tomado uma bebida alcoólica , é, numa
certa unidade , igual ao quociente entre o peso do álcool ingerido (em gramas) e 70% do peso dessa pessoa
(em quilogramas ) .
• num decilitro de um certo tipo de vinho existem 5 gramas de álcool.
Qual das expressões seguintes dá o nível de álcool no sangue de uma pessoa, em função do seu peso x (em
quilogramas ), uma hora depois de essa pessoa ter bebido dois decilitros desse vinho ?
2
(A) 70 x
Prof. Deolinda Sá
10
(B) 0.7 x
10
(C) 70 x
(D)
2
0 .7 x
Página 1 de 2
II Parte
x − 3 y +1
1. Seja r a recta definida pelas equações
=
= z e α o plano de equação 2 x + y = 1 .
2
3
1.1 Mostre que a recta r não é paralela nem perpendicular ao plano
1.2 Determine analiticamente o ponto comum à recta r e ao plano
α
1.3 Escreva uma equação do plano β paralelo ao plano
α.
α.
e que contenha a origem do referencial.
1.4 Considere o cone recto da figura. Suponha que a base está contida no
plano
D
α e que [EC] é um diâmetro da base, sendo C(0,1,0) e E(2,-3,2).
Determine as coordenadas de um ponto D, como ilustra a figura e que
satisfaça as condições atrás descritas e para esse ponto calcule o volume
C
E
do respectivo cone.
2. Considere a função
f representada graficamente na figura ao lado.
2.1 Indique o domínio e o contradomínio da função e escreva equações das assimptotas do gráfico da função.


3
 pertence ao gráfico, indique uma
2
expressão analítica que defina a função f .
2.2Sabendo que o ponto B  0,−
y
2
5
2.3 Indique, justificando, o valor lógico das seguintes frases:
2.3.1
x
-2
f é crescente em R \ {1}
2.3.2
∃x ∈ R : f ( x) = −2
-4
f (− x ) = − f (x ), ∀x ∈ R \ {1}
2.3.3
2.3.4
lim f ( x) = 1
x → +∞
− 4 x 2 + 11x − 6
2x 2 − 6x + 4
b
2.4.1 Simplifique a expressão analítica, escreva-a na forma h( x ) = a +
e indique o domínio em
x+d
2.4 Considere a função real de variável real definida por
h( x ) =
que essa simplificação é válida.
2.4.2 Sabendo que a expressão simplificada de h é equivalente no domínio de h à da função
diga, justificando, se os gráficos das funções
2.4.3 Resolva a equação:
h( x) +
f
f e h são iguais.
x
=1
1− x
3. Dia 1 de Janeiro de 2009 foi lançado num certo hipermercado um produto que vamos chamar A. Estima-se que
ao fim de t meses, ele detenha uma percentagem do mercado, dentro dos produtos similares vendidos nesse
hipermercado dada por:
P(t ) = 80 −
70
,t >o
t +1
Recorrendo a métodos analíticos:
3.1 Qual é a percentagem de mercado que este produto A deve atingir no fim do 1º trimestre de 2009?
(Apresente o resultado aproximado às unidades)
3.2 Determine em que mês o produto A terá 70% do mercado?(Apresente todos os cálculos)
3.3 Num outro hipermercado, existe um produto B cuja quota, no hiper onde é vendido, é dada em % por:
C (t ) = 70 −
20
, com t em meses, correspondendo t=0 a 1 de Janeiro de 2009.
t+4
Determine em que mês a percentagem de mercado do produto A ultrapassa a do produto B. Na 1ª ou na
2ª quinzena desse mês? (Apresente todos os cálculos)
Prof. Deolinda Sá
Página 2 de 2