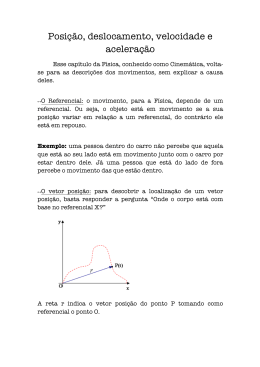
Prefixos do SI
A cinemática é a
parte da mecânica que
estuda os movimentos
dos corpos, sem mencionar suas causas.
Veja agora alguns
conceitos básicos
para a cinemática.
Ponto Material ou Partícula→
Quando as dimensões do corpo são
desprezíveis perante o problema
em questão.
Ex.: um ca-melo no deserto, avião
que vai de São Paulo a Londres,
...
Corpo Extenso→ Quando as
dimensões do corpo são
relevantes perante o problema
em questão.
Ex.: avião num hangar, carro na
garagem, ...
Referencial: Sistema em relação
ao qual consideramos a situação
em que um móvel se encontra.
Ex.: Em frente ao estádio, no
marco 411km de uma estrada, ...
z
y
x
Sistema Cartesiano
de Referência
Na Terra a
posição pode
ser dada por
dois ângulos
Movimento
Referencial
Repouso
Trajetória
Referencial
Nesta foto de
longa exposição
temos gravadas com
luz as trajetórias
dos veículos. Em
relação a que
referencial?
O solo.
•Distância Percorrida (d): Medida sobre a
trajetória, é a distância que o móvel
efetivamente percorreu.
•Deslocamento (Δx): Vetor cuja origem está
na posição inicial e extremidade na posição
final.
  
x  x  x0
Velocidade
Média(vm)
  

x x  x0
vm 

t
t  t0
***Assim é definido
em nossa região.
Velocidade Escalar
Média(vm)
d
vm 
t
v+
v-
Aceleração Escalar Média(am):
Expressa a rapidez com que o valor
da velocidade varia.
v
am 
t
vF  vi
am 
t F  ti
No SI → m/s2
***Uma aceleração escalar de
1m/s2 significa que a
velocidade varia 1m/s a cada
segundo que passa.
Classificação dos Movimentos
Movimento Retilíneo
Uniforme → M.R.U
Móvel percorre espaços iguais
em tempos iguais.
Sua velocidade não varia, o que
faz de sua aceleração nula.
No M.R.U.
Δx → Espaço percorrido
x→ Espaço final
x0→ Espaço inicial
Δx = x – x0
Δx = v.t
x – x0 = v.t => x = x0 + v.t
t=0
10
x0
t=1s
30
20 m
t=2s
t=3s
50
70
20 m
20 m
Daria pra fazer alguma previsão sobre
as posições futuras deste móvel?
v = 20 m/s
x0 = 10 m
x = x0 +v.t
x = 10 +20.t (SI)
Quando não importa o
sentido do movimento, usamos
d = v.t
A função horária das posições é dada por
Gráfico Espaço x tempo
Δx
Δt
x = x0 + v.t
x
v
t
N
 v  tg
Gráfico Velocidade x tempo
v
N
Δx
x  Avxt
t
Visto que no M.R.U. não há
aceleração, o gráfico é sempre
zero.
Problemas de encontro: Escrevemos a
função horária do espaço para os dois
móveis envolvidos no problema e depois
igualamos as duas, afinal só há encontro
quanto dois móveis estiverem na mesma
posição.
xA = xB
x0A+vA.t = x0B+vB.t
Pode-se também resolver por
velocidade relativa.
Velocidade Relativa→ drel = vrel.t
A
vA
B
vB
dREL
Mesma direção e
mesmo sentido
vrel= |va|-|vb|
Mesma direção e
sentidos contrários
vrel= |va|+|vb|
t=0
t=1s
v0=0
t=2s
t=3s
t=4s
4 m/s
8 m/s
0
2m
12 m/s
16 m/s
2
6m
8
10m
18
2+4
14m
6+4
32
10 + 4
a = 4 m/s2
*Note que a cada segundo v sofre a mesma
variação!!!
x(m)
Prof. Humberto
M.R.U.V
Equações do M.U.V.
1 2
1 2
x  x0  v0t  at  x  v0t  at
2
2
v  v0  at
v2  v02  2ax
***Propriedade do
MUV
***Qualquer
Movimento
vm 
Equação de
Torricelli
v  v0
2
vm 
x
t
x v  v0

t
2
Gráfico Espaço x Tempo
s
a<0
s
t
s
a>0
s0
t
ti
t
Instante da inversão
de sentido => v = 0
Gráfico Velocidade x Tempo
v
v
a>0
t
Δv
v0
θ
Δt
v
t
N
v
a
 a  tg
t
a<0
t
Gráfico Velocidade x tempo
v
N
v0
x  Avxt
Δx
t
Gráfico Aceleração x Tempo
a
a
N
v  Aaxt
Δv
t
M.R.U.V - gráficos