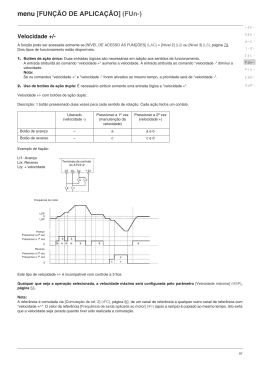
CONTROLO DE SISTEMAS – FORMULÁRIO (1/2)
Resposta no tempo
Resposta em frequência
Resposta em frequência: sistemas de 1ª ordem
1
𝐺(𝑠) =
𝐺(𝑠) = 𝑠
𝑠
Resposta no tempo: sistemas de 1ª ordem
1
𝐺(𝑠) =
1 + 𝜏𝑠
y(t)
1
inclinação (tangente na origem) de 1/τ
98.2%
95.0%
99.3%
86.5%
63.2%
0,5
𝐺(𝑠) =
0
1t
0
2t
3t
4t
5t
1
𝑇𝑠 + 1
𝐺(𝑠) = 𝑇𝑠 + 1
6t
t
Resposta ao degrau ℎ(𝑡):
𝑦(𝑡) = (1 − 𝑒 −𝑡⁄𝜏 ). ℎ(𝑡)
Resposta no tempo: sistemas de 2ª ordem
Resposta em frequência: sistemas de 2ª ordem
𝜔𝑛2
𝐺(𝑠) = 2
, com 𝜉 < 1
𝑠 + 2𝜉𝜔𝑛 𝑠 + 𝜔𝑛2
𝜔𝑛2
𝐺(𝑠) = 2
, com 𝜉 < 1
𝑠 + 2𝜉𝜔𝑛 𝑠 + 𝜔𝑛2
y(ω n t)
2
x=0.1
1,5
x=0.5
x=0.7
1
x=2.0
0,5
x=1.0
0
0
5
10
15
20
ωn t
Resposta ao degrau ℎ(𝑡):
𝑦(𝑡) = (1 − 𝑒 −𝜉𝜔𝑛 𝑡 cos (√1 − 𝜉 2 𝜔𝑛 𝑡)
−
𝜉𝑒 −𝜉𝜔𝑛 𝑡
√1 − 𝜉 2
sin (√1 − 𝜉 2 𝜔𝑛 𝑡)) ℎ(𝑡)
𝜔𝑑 = √1 − 𝜉 2 𝜔𝑛 (amortecida = damped)
1
𝜓=
𝜉𝜔𝑛
𝜋
Tempo de pico: 𝑡𝑝 = , 𝑦(𝑡𝑝 ) = 𝑦max
Frequência de ressonância: 𝜔𝑟 = 𝜔𝑛 √1 − 2𝜉 2
𝜔𝑑
Tempo de crescimento: 𝑡𝑟 =
𝜋−𝛽
𝜔𝑑
,
Tempo de estabelecimento: 𝑡𝑠 = 4𝜓
sendo 𝛽 = arctg
𝜔𝑑
𝜉𝜔𝑛
(critério de 2%)
Máximo sobre-impulso (overshoot): 𝑀𝑝 = exp (−
𝜉
√1−𝜉 2
𝜋)
Pico de ressonância:
𝑀𝑟 = 20 log10 (2𝜉√1 − 𝜉 2 )−1
Fase de ressonância:
𝜙𝑟 = −90𝑜 + arcsin (
𝜉
√1−𝜉 2
)
Margens de estabilidade
Margem de ganho:
MG = −20 log10 |𝐾𝐺(𝑗𝜔𝑐𝑓 )|,
𝜔𝑐𝑓 : arg[𝐾𝐺(𝑗𝜔)] = −180𝑜
Margem de fase:
MF = 180𝑜 + arg[𝐾𝐺(𝑗𝜔)], 𝜔𝑐𝑔 : |𝐾𝐺(𝑗𝜔)| = 1
CONTROLO DE SISTEMAS – FORMULÁRIO (2/2)
Regras para o Traçado do Lugar Geométrico das Raízes
Regras gerais:
 A função de transferência 𝐺(𝑠) tem n polos, 𝑝𝑗 (𝑗 = 1, … , 𝑛), e m zeros, 𝑧𝑖 (𝑖 = 1, … , 𝑚).
 O número de ramos do LGR e igual ao número de raízes da equação característica. Como se supõe sempre que 𝑛 ≥ 𝑚, o número
de ramos do LGR e sempre igual ao número de polos de 𝐺(𝑠), ou seja 𝑛.
 Todos os ramos do LGR começam nos polos de 𝐺(𝑠), para 𝐾 = 0, e terminam nos zeros de 𝐺(𝑠), para 𝐾 = ∞. Se o número de
polos for maior que o número de zeros, i.e., 𝑛 > 𝑚, então existirão (𝑛 − 𝑚) ramos que terminam no infinito.
 O LGR e sempre simétrico em relação ao eixo real.
 Se 𝑛 ≥ 𝑚 + 2, o “centro de gravidade” do caminho dos polos no LGR e constante qualquer que seja o 𝐾:
∑𝑛𝑗=1 Re(𝑝𝑗 ) = constante
LGR para o caso: 𝑲 ∈ ]𝟎, +∞[
1. Marcar no plano complexo os 𝑛 polos (×) e os 𝑚 zeros (𝑜)
de 𝐺(𝑠).
2. Um ponto do eixo real pertence ao LGR se a soma do
número de polos e zeros (reais e complexos) a sua direita
for impar.
3. As (𝑛 − 𝑚) assimptotas dos ramos do LGR que terminam no
infinito sao rectas que fazem um angulo com o eixo real,
contado no sentido direto (em graus), de:
180(1 + 2𝑘)
𝛾 =
,
𝑛 >𝑚
𝑛−𝑚
𝑘 = 0 (1ª assimptota), 𝑘 = 1 (2ª assimptota), … , até 𝑘 =
(𝑛 − 𝑚) − 1 (última assimptota).
4. As assimptotas do LGR intersectam-se num ponto do eixo
real dado por:
∑𝑛𝑗=1 Re(𝑝𝑗 ) − ∑𝑚
𝑖=1 Re(𝑧𝑖 )
𝜎𝑐 =
, 𝑛>𝑚
𝑛−𝑚
onde 𝑝𝑗 e 𝑧𝑖 correspondem aos 𝑛 polos e 𝑚 zeros de 𝐺(𝑠),
respectivamente.
5. Os pontos de convergência/divergência do LGR sobre o eixo
real correspondem as raízes reais da seguinte equação:
𝑑 −1
[𝐺 (𝑠)] = 0
𝑑𝑠
6. O ângulo de saída de um ramo do LGR num polo complexo,
𝜙𝑙 , e o ângulo de chegada de um ramo do LGR a um zero
complexo, 𝜓𝑙 , contados no sentido directo (em graus), são
obtidos respetivamente por:
𝑛
𝑚
𝜙𝑙 = 180° − ∑ 𝜙𝑗 + ∑ 𝜓𝑖
𝑗≠𝑙
𝑚
𝑖=1
𝑛
𝜓𝑙 = 180° − ∑ 𝜓𝑖 + ∑ 𝜙𝑗
𝑖≠𝑙
𝑗=1
Aproximação de Padé de 1ª ordem: 𝑒 −𝜃𝑠 ≈
Coeficientes de erro estático
Posição: 𝐾𝑝 = lim 𝐺(𝑠)
𝑠→0
Velocidade: 𝐾𝑣 = lim 𝑠𝐺(𝑠)
𝑠→0
Aceleração: 𝐾𝑎 = lim 𝑠 2 𝐺(𝑠)
𝑠→0
Critério de Nyquist: 𝑍 = 𝑁 + 𝑃
𝜃
1− 2 𝑠
𝜃
2
1+ 𝑠
LGR para o caso: 𝑲 ∈ ] − ∞, 𝟎[
1. Igual ao caso anterior.
2. Um ponto do eixo real pertence ao LGR se a soma do
número de zeros e polos (reais e complexos) a sua direita
for par.
3. As (𝑛 − 𝑚) assimptotas dos ramos do LGR que terminam no
infinito são retas que fazem um angulo com o eixo real,
contado no sentido direto (em graus), de:
360𝑘
𝛾=
, 𝑛>𝑚
𝑛−𝑚
𝑘 = 0 (1ª assimptota), 𝑘 = 1 (2ª assimptota), …, até 𝑘 =
(𝑛 − 𝑚) − 1 (ultima assimptota).
4. Igual ao caso anterior.
5. Igual ao caso anterior.
6. O ângulo de saída de um ramo do LGR num polo complexo,
𝜙𝑙 , e o ângulo de chegada de um ramo do LGR a um zero
complexo, 𝜓𝑙 , contados no sentido direto, são obtidos
respetivamente por:
𝑛
𝑚
𝑚
𝜙𝑙 = − ∑ 𝜙𝑗 + ∑ 𝜓𝑖 ,
𝑗≠𝑙
𝑛
𝜓𝑙 = − ∑ 𝜓𝑖 + ∑ 𝜙𝑗
𝑖=1
Outras notas:
𝑖≠𝑙
𝑗=1
CONTROLO DE SISTEMAS – DIAGRAMA DE BODE
Bode Diagram
80
60
40
Magnitude (dB)
20
0
-20
-40
-60
-80
270
180
Phase (deg)
90
0
-90
-180
-270
-3
10
-2
10
-1
10
0
10
Frequency (rad/sec)
1
10
2
10
3
10