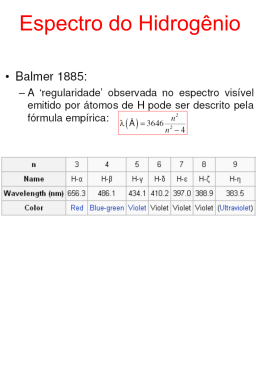
O Átomo de Hidrogênio
Equação de Schrödinger em coordenadas esféricas:
 2 2

  V r   r ,  ,    E   r , ,  

 2

Separação de variáveis:
r, ,    Rr  F    
Y  ,  
O Átomo de Hidrogênio
Substituindo na Eq. Schrödinger obtemos 3 equações:
d 2
d 2
  m 2
Equação Azimutal
m 2 
1 d 
dF  
 sen
    1 
F  0
2
sen d 
d  
sen  
Equação de Colatitude
1 d  2 dR   2
  1
r
R0
   2 E  V r  

2 dr 
2
r
r
 dr   

Equação Radial
Átomo de hidrogênio
A Função Angular
As soluções das equações angulares (azimutal e colatitude) são
dadas por:
   Aeim ; m  0,  1,  2, ...
F    BP
m

cos ;
  0,1, 2, ... m  
Função angular:
Y  ,   
m
BP
cos  Ae
 Y  ,  dd  1 
im
encontramos AB
A Função Radial
No caso geral, a solução é dada por:

 r 
 r  2  1
 exp 
  Ln   r 
Rn r   
 nr0 
 nr0 
n  1, 2, 3,...
número quântico principal
n 1  
O número quântico n define a energia do átomo, da mesma
forma que no modelo de Bohr:
13 .6
E   2 eV
n
A Função Radial
Exemplos
Interpretação da função angular
L está relacionado à grandeza momento angular orbital e
seu módulo é quantizado:
L   1
  0,1, 2, ...,n 1
número quântico orbital
Lz é a componente na direção z do momento angular orbital
Lz  m
m  0,  1,  2, ..., 
número quântico magnético
A Função Angular
Exemplo:
2
L  22 1  6
Lz  m, m  0, 1, 2
Observe que:
- Tanto o módulo quanto a componente z
do momento angular são quantizados
A Função Angular
  0, m  0
1
Y00  ,   
4
Quando l = 0, a função de onda exibe simetria esférica.
A Função Angular
  1, m  0
3
Y10  ,   
cos
8
  1, m  1
3
Y11  ,   
sen e i
8
Quando l = 1, a função de onda exibe simetria em torno do
eixo z.
A Função Angular
Portanto, o par (l, ml) define o tipo de simetria da função de
onda:
0
 1
2
3
Orbital (s)
Orbital (p)
Orbital (d)
Orbital (f)
Resumo: Átomo de Hidrogênio
• Elétron confinado em 3 dimensões: 3 números quânticos
• n determina a energia do átomo
• l e ml determinam o momento angular do átomo e e a
simetria da função de onda
O elétron possui um número quântico intrínseco de
“spin”, formando um total de 4 números quânticos
S z  mS 
1
mS  
2
Átomos de muitos elétrons
São descritos pelos mesmos números quânticos que o átomo
de hidrogênio
E  f n, 
Como preencher os níveis de energia?
PRINCÍPIO DA EXCLUSÃO DE PAULI: cada estado só pode
ser ocupado por, no máximo, 1 elétron
MÍNIMA ENERGIA: os estados ocupados são sempre os de
menor energia possível
LEI DE HUND: Deve-se maximizar o spin desde que os
princípios anteriores não sejam violados.
Átomos de muitos elétrons
Número de estados possíveis:
  2  1 2
n 1
n   2  1 2
 0
n = 1: 2 estados
n = 2: 8 estados
n = 3: 18 estados
Número de elementos por linha da
tabela periódica!
Átomos de muitos elétrons
Exercícios
1) Considere as funções de onda a seguir, que representam dois estados distintos de um átomo de hidrogênio:
 1 r , ,   
1
 r0 3 / 2
 2 r , ,   
e
r / r0
1
8  r0 3 / 2

 r   r n r0 2 1
 e
 Ln   r   Pm cos    e im
 nr0 
 r , ,    k 
r r / 3r0 
r 
 6   sen e i
e
r0
r0 

Considere que um elétron se encontrava inicialmente no estado descrito por 2 e, após emitir
espontaneamente um fóton, passou a ocupar o estado descrito por 1.
Determine:
a) A energia do fóton emitido.
b) O número total de estados nos quais a energia de ionização do elétron é a mesma que a representada
pelo estado 2.
d) A probabilidade de o elétron ser encontrado na região x > 0, após a emissão do fóton.
e) A probabilidade de que, após a emissão do fóton ter ocorrido, o átomo emita espontaneamente um outro
fóton em um tempo inferior a 10 ms.
2) Para cada uma das afirmativas abaixo, determine se ela é verdadeira (V) ou falsa (F).
a) Os números quânticos n = 2, l = 0, ml = 0 e ms = -1/2 descrevem o estado do elétron mais energético
do átomo de carbono no estado fundamental.
b) Dois átomos de hidrogênio no estado fundamental possuem, necessariamente, o mesmo valor de
momento angular total.
c) Se dois elétrons de comprimentos de onda iguais a 10 e 5 angstroms incidem numa barreira de potencial, o
primeiro tem maior probabilidade de atravessá-la do que o segundo.
d) O elétron, por possuir massa, sempre se comporta como partícula, enquanto o fóton, que não possui
massa,
pode se comportar tanto como partícula como quanto onda, dependendo do experimento.