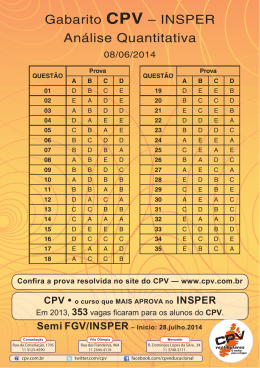
CPV O Cursinho que Mais Aprova na GV
FGV ADM – Objetiva – Prova A – 09/dez/2012
MATEMÁTICA
01. O PIB per capita de um país, em determinado ano, é o PIB
daquele ano dividido pelo número de habitantes.
Se, em um determinado período, o PIB cresce 150% e a
população cresce 100%, podemos afirmar que o PIB per
capita nesse período cresce.
a)20%
b)25%
c)35%
d)45%
e)50%
Resolução:
O PIB per capita é dado por PIB , onde h é o número de habitantes.
h
Com os aumentos dados no enunciado, o novo PIB per capita
é
(1 + 150%) . PIB
= 1,25 . PIB , o que representa 25% de
(1 + 100%) . h
h
crescimento em relação ao PIB per capita sem os aumentos.
Alternativa B
02. Um capital A de R$ 10.000,00 é aplicado a juros compostos,
à taxa de 20% ao ano; simultaneamente, um outro capital B,
de R$5.000,00, também é aplicado a juros compostos, à taxa
de 68% ao ano.
Utilize a tabela abaixo para resolver.
x
1
2
log x
0
0,30 0,48 0,60 0,70 0,78 0,85 0,90 0,96
3
4
5
6
7
8
Depois de quanto tempo os montantes se igualam?
a)
b)
c)
d)
e)
9
22 meses.
22,5 meses.
23 meses.
23,5 meses.
24 meses.
Resolução:
Montante A: 10.000 (1,2)t
Montante B: 5.000 (1,68)t
Para os montantes serem iguais, temos:
10.000 . (1,2)t = 5.000 . (1,68)t
 1, 68 t

2 = 
 1, 2 
2 = 1,4t
log 2 = t (log 2 + log 7 – log 10)
0,30 = t (0,30 + 0,85 – 1)
0,30 = 0,15t
t = 2 anos
Portanto, 24 meses
CPV
FGVADMDEZ2012
Alternativa E
1
2
CPV
FGV – 09/12/2012
o
Cursinho
03. A equação x– 4 =16 tem
a)
b)
c)
d)
duas raízes reais e duas raízes imaginárias conjugadas.
pelo menos duas raízes iguais.
uma única raiz imaginária.
quatro raízes reais.
1
e) quatro raízes cujo produto é – .
4
Resolução:
que
Mais Aprova
na
GV
05. Desenvolvendo-se o binômio P( x ) =( x +1)5, podemos dizer
que a soma de seus coeficientes é:
a)16
b)24
c)32
d)40
e)48
Resolução:
x4 –
 2 1  2 1
1
= 0 Þ  x +  .  x −  = 0
16
4
4
Para saber a soma dos coeficientes de um polinômio basta fazer
o P(1):
x2 +
1
1
=0 Þ x=± i
4
2
P(x) = (x + 1)5 Þ
P(1) = (1 + 1)5 = 32
Alternativa C
ou
x2 –
S=
06. Um anfiteatro tem 12 fileiras de cadeiras. Na 1a fileira há 10
lugares, na 2a há 12, na 3a há 14 e assim por diante (isto é,
cada fileira, a partir da segunda, tem duas cadeiras a mais que
a da frente).
1
1
=0 Þ x=±
4
2
{ ± 12 ; ± 12 i }
Alternativa A
04. Se uma pessoa faz hoje uma aplicação financeira a juros
compostos, daqui a 10 anos o montante M será o dobro do
capital aplicado C.
Utilize a tabela abaixo.
0
0,1
0,2
0,3
0,4
2x
1
1,0718
1,1487
1,2311
1,3195
Qual é a taxa anual de juros?
a)6,88%
b)6,98%
c)7,08%
d)7,18%
e)7,28%
Para que o montante seja o dobro, temos:
2C = C (1 + i)10 Þ 2 = (1 + i)10 Þ 21/10 = 1 + i
Þ 1,0718 = 1 + i Þ i = 0,0718
Portanto, a taxa anual será de 7,18%.
Alternativa D
FGVADMDEZ2012
a)250
b)252
c)254
d)256
e)258
O total de cadeiras é dado pela soma dos 12 termos de uma P.A.
cujo a1 = 10, r = 2 e a12 = 10 + (12 – 1) . 2 = 32, ou seja:
S12 = (10 + 32) .
Resolução:
CPV
O número total de cadeiras é:
Resolução:
x
12
= 252 cadeiras
2
Alternativa B
CPV
o
C ursinho
que
Mais Aprova
na
GV
FGV – 09/12/2012
3
07. Um triângulo isósceles tem os lados congruentes com medida
igual a 5. Seja α a medida do ângulo da base, para a qual a
área do referido triângulo é máxima.
09. Quatro pessoas devem escolher ao acaso, cada uma, um único
número entre os quatro seguintes: 1, 2, 3 e 4. Nenhuma fica
sabendo da escolha da outra.
Podemos afirmar que
a)10º ≤ α < 20º
b)20º ≤ α < 30º
c)30º ≤ α < 40º
d)40º ≤ α < 50º
e)50º ≤ α < 60º
1
a) 256
1
b) 128
Resolução:
1
c) 64
180º – 2α
5
1
d) 32
5
α
1
e) 16
α
A área do triângulo é dada por:
1
25
S=
. 5 . 5 . sen (180º – 2α) =
. sen 2α
2
2
Como 0º < α < 90º, a área é máxima para:
sen 2α = 1 Þ 2α = 90º
Logo, 40º ≤ α < 50º
Þ
Resolução:
α = 45º
Para que as quatro pessoas escolham o mesmo número, as escolhas
das 2a, 3a e 4a pessoas, devem ser iguais à da 1a, independente de
qual número ela tenha escolhido, assim:
a21a 3a 4a
Alternativa D
08. Um reservatório tem a forma de uma esfera. Se aumentarmos
o raio da esfera em 20%, o volume do novo reservatório, em
relação ao volume inicial, aumentará
A probabilidade de que escolham quatro números iguais é:
4 1 1 1
1
. . . =
64
4 4 4 4
Alternativa C
a)60%
b)63,2%
c)66,4%
d)69,6%
e)72,8%
Resolução:
Chamando de R o raio inicial da esfera, após o seu aumento temos
1,2.R, Assim:
Vinicial =
Vfinal =
4
. π . R3
3
4
4
. π . (1,2.R)3 = 1,728 . π . R3
3
3
Assim, Vfinal = 1,728 . Vinicial, que representa um aumento de
72,8%.
Alternativa E
FGVADMDEZ2012
CPV
4
CPV
FGV – 09/12/2012
o
Cursinho
10. Um triângulo tem lados medindo 1cm, 2cm e 2,5cm. Seja h
a medida da altura relativa ao maior lado.
O valor de h2 expresso em cm2 é, aproximadamente, igual a
a)0,54
b)0,56
c)0,58
d)0,60
e)0,62
que
Mais Aprova
Resolução:
Resolução:
1
h
x
2
2,5 – x
Logo:
1 = h2 + (0, 65)2 Þ h @ 0,58
Alternativa C
a)7
b)8
c)9
d)10
e)11
A solução da equação X . A = B é :
X = B . A–1
Assim, temos:
 3 − 1
 = [9 – 2]
X = [8 3] 
− 5
2 

Portanto, a soma dos elementos de X é 7.
Assim, temos:
I.22 = h2 + (2,5 – x)2
Þ I – II Þ x = 0,65
II.12 = h2 + x2
GV
 3 −1 
,
11. Sabendo que a inversa de uma matriz A é A–1 = 
−5 2


e que a matriz X é solução da equação matricial X . A = B, em
que B = [8 3], podemos afirmar que a soma dos elementos
da matriz X é:
Montando o triângulo temos:
na
Alternativa A
12. No plano cartesiano, há duas retas paralelas à reta de
equação 3x + 4 y + 60 = 0 e que tangenciam a circunferência
x2 + y2 = 4.
Uma delas intercepta o eixo y no ponto de ordenada
a)2,9
b)2,8
c)2,7
d)2,6
e)2,5
Resolução:
A equação das retas paralelas é 3x + 4y + c = 0 e como elas
tangenciam a circunferência x2 + y2 = 4, temos:
dcentro, reta = raio
3.0+4.0+c
= 2 Þ | c | = 10
Þ
Þ c = 10 ou c = –10
Assim, as equações das retas são
3x + 4y + 10 = 0 e 3x + 4y – 10 = 0,
e interceptam o eixo y nos pontos (0; –2,5) e (0; 2,5), respectivamante.
32 + 42
Alternativa E
CPV
FGVADMDEZ2012
CPV
o
C ursinho
que
Mais Aprova
na
GV
FGV – 09/12/2012
5
13.Uma única linha aérea oferece apenas um voo diário da
cidade A para a cidade B. O número de passageiros y que
comparecem diariamente para esse voo relaciona-se com o
preço da passagem x , por meio de uma função polinomial
do primeiro grau.
14. O par ordenado (x; y) que satisfaz o sistema de equações
 1 3
 x − y = 9

 2
5
 + = − 4
x
y

Quando o preço da passagem é R$ 200,00, comparecem
120 passageiros e, para cada aumento de R$ 10,00 no preço
da passagem, há uma redução de 4 passageiros.
Qual é o preço da passagem que maximiza a receita em
cada voo?
a)
b)
c)
d)
e)
R$ 220,00
R$ 230,00
R$ 240,00
R$ 250,00
R$ 260,00
é tal que sua soma x + y vale
a)
1
7
1
b)
- 6
1
c)
- 5
1
d)
- 4
e)
-
Resolução:
1
3
Temos que, a função que relaciona y com x pode ser representada
por:
y = Ax + B
Resolução:
Do enunciado temos:
Sejam a =
120 = 200 A + B
−

116 = 210 A + B
Þ
y = – 0,4x + 200
 1 3
 x − y = 9
a − 3b = 9

⇒ 
 2
2a + 5b = − 4
5
 + = − 4
x
y

Como a receita é dada por:
Resolvendo o sistema linear, obtemos a = 3 e b = –2.
R = x . y = – 0,4x2 + 200x
Assim, x =
Portanto, o preço que maximiza a receita é:
200
xv = –
= 250
2 . (−0, 4)
⇒ A = − 0, 4 e B = 200
1
1
e b = , temos:
y
x
1
1
e y=–
3
2
Logo, x + y =
1 1
- =–1
3 2
6
Alternativa B
Alternativa D
FGVADMDEZ2012
CPV
6
FGV – 09/12/2012
CPV
o
Cursinho
15. No plano cartesiano, considere o triângulo de vértices
A (1; 4), B ( 4; 5) e C (6; 2) .
A reta suporte da altura relativa ao lado AC intercepta o eixo
x no ponto de abscissa
a)2
b)2,2
c)2,4
d)2,6
e)2,8
B
A
H
C
x
4− 2
2
=−
1− 6
5
Como BH
AC, mAC . mBH = – 1 Þ mBH =
5
2
5
2
5
5x
Þ y – 5 = (x – 4) Þ y =
–5
2
2
B(4; 5)
mBH =
Calculando o ponto em que a reta intercepta o eixo x:
0=
CPV
5
x–5 Þ x=2
2
FGVADMDEZ2012
na
GV
COMENTÁRIO DA PROVA DE MATEMÁTICA
A Prova de Matemática da FGV Administração Dezembro 2012
manteve os mesmos moldes do semestre anterior.
O nível de dificuldade das questões esteve dentro do previsto,
privilegiando o aluno bem preparado.
A distribuição dos assuntos abrangeu praticamente todo o
conteúdo programático:
y
Mais Aprova
Os enunciados de todas as questões foram claros, não deixando
margem a dúvidas.
Resolução:
mAC =
que
Alternativa A
1 questão de Equações Algébricas
1 questão de Função do 2o Grau
1 questão de Polinômios
1 questão de Progressão Aritmética
1 questão de Probabilidades
1 questão de Matrizes
1 questão de Sistemas
3 questões envolvendo Porcentagem e Juros (Matemática Financeira)
2 de Geometria Plana
2 de Geometria Analítica
1 de Geometria Espacial
A equipe do CPV parabeniza a Banca Examinadora da FGV
pela elaboração da prova, que deve cumprir
a finalidade de selecionar os melhores candidatos nesta Prova
Objetiva.