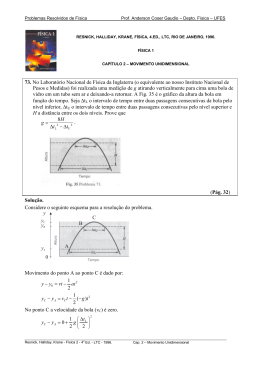
Problemas Resolvidos de Física
Prof. Anderson Coser Gaudio – Depto. Física – UFES
RESNICK, HALLIDAY, KRANE, FÍSICA, 4.ED., LTC, RIO DE JANEIRO, 1996.
FÍSICA 1
CAPÍTULO 6 – DINÂMICA DA PARTÍCULA
52. Uma bola de 1,34 kg está presa a uma haste rígida vertical por meio de dois fios sem massa, de
1,70 m de comprimento cada. Os fios estão presos à haste em pontos separados de 1,70 m. O
conjunto está girando em volta do eixo da haste, com os dois fios esticados formando um
triângulo eqüilátero com a haste, como mostra a Fig. 45. A tensão no fio superior é 35,0 N. (a)
Encontre a tensão no fio inferior. (b) Calcule a força resultante na bola, no instante mostrado na
figura. (c) Qual é a velocidade da bola?
(Pág. 120)
Solução.
Considere o seguinte esquema da situação:
T1
l
θ
m
r
l
a
y
θ
m
v
x
T2 θ
P
l
(a) Forças na bola em y:
∑F
y
=0
T1 cos θ − T2 cos θ − P =
0
T2 =
T1 −
mg
8, 7092 N
=
cos θ
________________________________________________________________________________________________________
Resnick, Halliday, Krane - Física 1 - 4a Ed. - LTC - 1996.
Cap. 6 – Dinâmica da Partícula
1
Problemas Resolvidos de Física
Prof. Anderson Coser Gaudio – Depto. Física – UFES
T2 ≈ 8, 7 N
(b) A força resultante (R) que atua na bola vale:
R = T1 + T2 + P
R = ( −T1 sen θ i + T1 cos θ j) + ( −T2 sen θ i − T2 cos θ j) + ( −mgj)
R=
− (T1 + T2 ) sen θ i + (T1 − T2 ) cos θ − mg  j
(1)
R=
− ( 37,8532 N ) i + 0 j
(2)
R ≈ − ( 38 N ) i
(c) A resultante calculada no item (b) é a força centrípeta do movimento circular da bola em torno
do eixo. Logo:
mv 2
r
A comparação das equações (1) e (2) nos dá o módulo de R:
Fc= R=
=
R
(T1 + T2 ) sen θ
(3)
(4)
Substituindo-se (4) em (3):
mv 2
mv 2
(T1 + T2 ) sen θ = =
r
l sen θ
(T1 + T2 ) l 6, 4489 m/s
=
=
v sen
θ
m
v ≈ 6, 4 m/s
________________________________________________________________________________________________________
Resnick, Halliday, Krane - Física 1 - 4a Ed. - LTC - 1996.
Cap. 6 – Dinâmica da Partícula
2