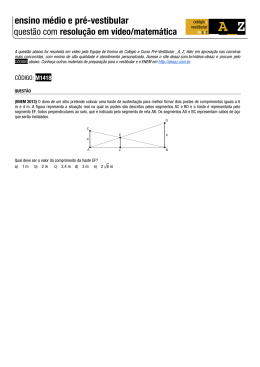
www.fisicaexe.com.br
Uma haste tem seu movimento limitado à vertical (para
cima e para baixo), esta haste está apoiada num plano
inclinado formado por uma cunha de um ângulo α que desliza
livremente sobre uma superfície horizontal, conforme figura ao
lado. A razão entre a massa da cunha pela massa da haste é
igual a r. Determinar as acelerações da haste e do plano
inclinado. Desprezam-se todos os atritos.
Dados do problema
•
•
razão entre as massas da cunha e da haste
ângulo do plano inclinado:
r;
α
Esquema do problema
O movimento da haste está limitado à direção vertical,
o peso da haste ( P A ) produz uma ação na cunha ( N ), esta
possui uma componente na direção horizontal com sentido
para a direita ( N x ). Como não há atritos a cunha deslizará
para a direita com aceleração a B e a haste descerá sob a
ação do seu próprio peso com aceleração a A .
Isolando os corpos e pesquisando as forças em cada
um deles, temos
figura 1
Haste (figura 2-A):
P A : força peso da haste;
N : reação do contato com o plano inclinado;
N PD : reação do contato com a parede direita;
N PE : reação do contato com a parede esquerda.
figura 2
Pela figura 2-B vemos que a força de reação do plano na haste forma um ângulo α com
a vertical.
Cunha (figura 3-A):
P B : força peso da cunha;
N : ação de contato haste;
1
www.fisicaexe.com.br
N C : reação do contato com chão;
figura 3
Pela figura 3-B vemos que a força de reação da haste no plano forma um ângulo α com
a vertical.
Solução
Desenhando as forças que agem nos corpos num sistema de eixos coordenados e
aplicando a 2.ª Lei de Newton
F = ma
(I)
Para a haste (figura 2-C), obtemos
NN PDN PEP A = m a A
onde
N = −N sen iN cos  j ;
N PD = −N PD i ;
N PE = N PE i;
P A = −m A g j ;
a A = m AaA j
assim
−N sen  iN cos j−N PD iN PE i−m A g j = m A a A j
(II)
Separando as componentes da expressão (II), temos
−N sen −N PDN PE = 0
N cos−m A g = m A a A
Aplicando a expressão (I) para a cunha (figura 3-C), obtemos
NN CP B = m a B
onde
N = N sen  i−N cos j ;
N C = N C j;
P B = −m B g j ;
aB = mBaBi
2
(III)
(IV)
www.fisicaexe.com.br
assim
N sen  i−N cos j−N C j−m B g j = m B a B i
(V)
Separando as componentes da expressão (V), temos
N sen  = m B a B
−N cos −N C−m B g = 0
(VI)
(VII)
As expressões (IV) e (VI) forma um sistema de dua equações a três incógnitas (N, a A e
a B – as massas m A e m B também não são conhecidas, mas o problema fornece a razão das
massas r.)
∣
N cos −m A g = m A a A
N sen  = m B a B
(VIII)
(IX)
Este sistema possui mais incógnitas do que equações, é uma sistema impossível, mas
a partir da Cinemática podemos encontrar uma relação entre as duas acelerações.
figura 4
Considerando um ponto B 1 no plano inclinado da cunha e um ponto A 1 no ponto de
contato da haste com a cunha num instante inicial (figura 4-A), escrevemos as funções horárias
do Movimento Retilíneo Uniformemente Variado (M.R.U.V.) para a haste e para a cunha,
vamos adotar que neste instante as velocidades iniciais dos corpos são nulas ( v A0 = v B0 = 0 ),
temos
aB 2
t
2
aB 2
x −x 0 = 0 t
t
2
aB 2
Δx =
t
2
2Δ x
2
t =
aB
x = x 0v B0 t 
aA 2
t
2
aA 2
y− y 0 = 0 t
t
2
aA 2
Δy =
t
2
2Δ y
t2 =
aA
y = y 0v A0 t 
e
O tempo que um ponto da cunha vai levar para se deslocar de B 1 até B 2 será o mesmo
intervalo de tempo que um ponto da haste vai levar para se deslocar de A 1 até A 2, podemos
igualar os tempos nas expressões acima (na verdade igualar o quadrado dos tempos)
2 Δx
2Δ y
=
aB
aA
Δy
aA = aB
Δx
Pela figura 4-B podemos relacionar os deslocamentos Δ x e Δ y pelo ângulo α
3
www.fisicaexe.com.br
Δ x = S cos 
Δ y = S sen
e
substituindo este valores, obtemos
S sen 
S cos
a A = −a B tg 
a A = aB
(X)
o sinal de negativo foi colocado porque a aceleração da haste está no sentido contrário do
referencial adotado (para cima).
Da expressão (IX), temos
N=
m Ba B
sen 
(XI)
substituindo (X) e (XI) em (VIII), obtemos
m Ba B
cos −m A g = −m A a b tg 
sen 
mBaB
−m A g = −m A a b tg
tg
mBaB
m A a b tg = m A g
tg
dividindo toda a expressão por m A e lembrando que a razão das massas é r =
m Ba B
 m A a b tg  = m A g
tg 
mB aB mA
mA

a tg  =
g
m A tg m A b
mA
aB
r
a b tg  = g
tg
1
aB r
tg = g
tg 
r tg 2 
aB
=g
tg 



aB =

g tg 
2
r tg 
substituindo este resultado na expressão (X)
2
aA=−
g tg 
2
r  tg 
4
: m A 
mB
, fica
mA