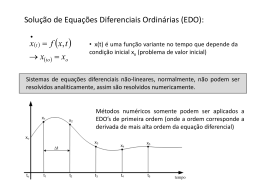
&DStWXOR±(TXDo}HV'LIHUHQFLDLV2UGLQiULDV
BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBB
&DStWXOR±(TXDo}HV'LIHUHQFLDLV2UGLQiULDV
Å
2 3UREOHPD GH &DXFK\ RX 3UREOHPD GH 9DORU ,QLFLDO 39,
x
2 SUREOHPD:
Determinar a função \
± &- ,
onde - denota um intervalo de ¸, que satisfaz,
\
IW\W W± -
\W \
x
x
Trata-se de um 3UREOHPDGH&DXFK\ de SULPHLUDRUGHP, por não ocorrerem
derivadas de ordem mais elevada.
À relação \W
\ chama-se FRQGLomRLQLFLDO ou FRQGLomRGHYDORULQLFLDO.
SRUH[HPSOR: o problema
\
\W
\ tem como VROXomR a função \
x
HW .
O Problema de Valor Inicial torna-se HTXLYDOHQWH à resolução da equação,
VHHVy se I for FRQWtQXD com respeito a W .
BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBB
$QiOLVH1XPpULFD5RViOLD5RGULJXHVH$QWyQLR3HUHLUD
&DStWXOR±(TXDo}HV'LIHUHQFLDLV2UGLQiULDV
BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBB
Å
([LVWrQFLD H 8QLFLGDGH GH 6ROXomR
x
GHILQLomR:
A função IW\satisfaz uma FRQGLomRGH/LSVFKLW] com
respeito a\ se existe uma FRQVWDQWH /
!
tal que,
_IW\±IW]_≤ / _\±]_
para todo oW±
- e para todos os reais \ e ].
A FRQVWDQWHGH/LSVFKLW]/ é independente de W.
x
WHRUHPD:
O Problema de Cauchy (PVI) de primeira ordem WHPXPD
~QLFDVROXomR \W para W
(1)
(2)
± -, se
IW\é FRQWtQXD em W e
IW\satisfaz uma FRQGLomRGH/LSVFKLW] com respeito a \.
BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBB
$QiOLVH1XPpULFD5RViOLD5RGULJXHVH$QWyQLR3HUHLUD
&DStWXOR±(TXDo}HV'LIHUHQFLDLV2UGLQiULDV
BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBB
Å
5HVROXomR 1XPpULFD ± 'LVFUHWL]DomR
x
x
x
x
Serão apenas determinados YDORUHVDSUR[LPDGRV da função \ num FRQMXQWR
GLVFUHWR de 1 pontos.
Fixe-se 7ˆ
Fazendo K
e seja -
>W W 7@
o LQWHUYDORGHLQWHJUDomR.
71obtemos uma PDOKDXQLIRUPHdo intervalo -.
K (amplitude dos subintervalos) chama-se SDVVRGHGLVFUHWL]DomR (ou
simplesmente SDVVR).
SDUDRPHVPRH[HPSOR:
\ H[
a solução exacta
e duas soluções aproximadas
obtidas:
pelo 0pWRGRGR3RQWR0pGLR
e pelo 0pWRGRGH(XOHU
ambas com K
x
Vamos representar a VROXomRH[DFWD \WQ no nóWQ simplesmente por \Q e a
x
assim,
x
Também representaremos,IQ
VROXomRQXPpULFDDSUR[LPDGD no mesmo nó por XQ,
\Q ≡ \WQ
XQ ≈ \Q
≡ IWQ XQ
e obviamente que X
\ .
BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBB
$QiOLVH1XPpULFD5RViOLD5RGULJXHVH$QWyQLR3HUHLUD
&DStWXOR±(TXDo}HV'LIHUHQFLDLV2UGLQiULDV
BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBB
>
7LSRV GH 0pWRGRV
x
GHILQLomR:
Um método numérico para a aproximação do PVI é designado de
3DVVR6LPSOHV se ∀
Q ≥ XQ GHSHQGHVy de XQ .
Caso contrário é designado um método de 3DVVR0~OWLSOR
(ou Multipasso).
x
GHILQLomR:
Um método numérico para a aproximação do PVI designa-se
H[SOtFLWR se XQ pode ser calculado directamente
em termos de valores XN ,
N ≤ Q.
Um método diz-se ser LPSOtFLWR se XQ depende
implicitamente de si próprio através de I .
BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBB
$QiOLVH1XPpULFD5RViOLD5RGULJXHVH$QWyQLR3HUHLUD
&DStWXOR±(TXDo}HV'LIHUHQFLDLV2UGLQiULDV
BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBB
Å
$OJXQV 0pWRGRV GH 3DVVR 6LPSOHV
¨ Método de (XOHU([SOtFLWRRXSURJUHVVLYR
x
A estratégia do método consiste em aproximar a GHULYDGD pela GLIHUHQoD
ILQLWDSURJUHVVLYD,
\¶W≈ \WK±\WK
\WK≈ \WK\¶W
\ W IW\W,
x
e como, pela definição de PVI,
x
ou, na representação que usamos para as aproximações,
x
\WK≈ \WKIW\W
XQ XQ KIQ
Deste modo, partindo de X
\ e para o passo K estipulado, é gerada
uma VXFHVVmRGHSRQWRV que aproximam a VROXomRH[DFWD.
BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBB
$QiOLVH1XPpULFD5RViOLD5RGULJXHVH$QWyQLR3HUHLUD
&DStWXOR±(TXDo}HV'LIHUHQFLDLV2UGLQiULDV
BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBB
x
SDUDRPHVPRH[HPSOR:
\
\ \[ H[ no intervalo >@
K pelo 0pWRGRGH(XOHU([SOtFLWR,
obter uma aproximação da solução
passo
\W
com
XQ XQ KIQ
u0 = 1
u1 = u0 + 0.25 f0 = 1.00000 + 0.25(1.00000) = 1.25000
u2 = u1 + 0.25 f1 = 1.25000 + 0.25(1.25000) = 1.56250
u3 = u2 + 0.25 f2 = 1.56250 + 0.25(1.56250) = 1.95313
u4 = u3 + 0.25 f3 = 1.95313 + 0.25(1.95313) = 2.44141
x
x
Comparando com os valores exactos, vemos que os resultados obtidos não
são muito satisfatórios ...
QK
XQ
HQK
Podemos conseguir resultados (um pouco) melhores para K
Q K
XQ
HQK
.
BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBB
$QiOLVH1XPpULFD5RViOLD5RGULJXHVH$QWyQLR3HUHLUD
&DStWXOR±(TXDo}HV'LIHUHQFLDLV2UGLQiULDV
BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBB
¨ Método de (XOHU,PSOtFLWRRXUHJUHVVLYR
x
x
x
Neste caso, a GHULYDGD é aproximada pela GLIHUHQoDILQLWDUHJUHVVLYD.
O método é análogo ao anterior e a precisão dos resultados obtidos é
semelhante.
Os HUURV verificados em ambos os métodos de Euler, resultam basicamente
da aproximação de um LQWHJUDO pela iUHDGHXPUHFWkQJXOR.
(XOHU ([SOtFLWR
(XOHU ,PSOtFLWR
¨ Método de &UDQN1LFROVRQRXGRWUDSp]LR
x
Neste caso, o integral é aproximado pela UHJUDGRWUDSp]LR
¨ Método de +HXQ
x
Este método consiste numa variação do anterior. Na regra do trapézio, o
termo IQ é substituído por IWQ XQ KIQ que corresponde ao
resultado do Método de Euler Explícito.
BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBB
$QiOLVH1XPpULFD5RViOLD5RGULJXHVH$QWyQLR3HUHLUD
&DStWXOR±(TXDo}HV'LIHUHQFLDLV2UGLQiULDV
BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBB
x
x
Å
Deste modo, um PpWRGRLPSOtFLWR foi transformado num PpWRGRH[SOtFLWR.
Os quatro métodos anteriores são casos particulares dos chamados
0pWRGRVGH7D\ORU, por poderem ser deduzidos através do
desenvolvimento de Taylor da função pretendida \W .
0pWRGRV GH 7D\ORU
x
Seja a HTXDomRGLIHUHQFLDO
com a FRQGLomRLQLFLDO
\
IW\WW ≤ W ≤ W 7,
\W \.
¨ 0pWRGRGH(XOHU([SOtFLWR
x
Fazendo K
71, consideremos o desenvolvimento de Taylor da função
\WK em torno de W,
x
Tomando apenas os dois primeiros termos e para cada W
x
que é a fórmula do 0pWRGRGH(XOHU([SOtFLWR, bem como a informação de
que o HUUR cometido depende da segunda derivada e é 2K .
WQ, temos,
BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBB
$QiOLVH1XPpULFD5RViOLD5RGULJXHVH$QWyQLR3HUHLUD
&DStWXOR±(TXDo}HV'LIHUHQFLDLV2UGLQiULDV
BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBB
x
H[HPSOR : Resolver pelo Método de Euler Explícito,
\
para W±\
\ ≤ W ≤ com K .
Partindo da relação,
( A solução é \W
HWW )
XQ XQ KIQ
XQ KWQ ± XQ ±KXQ KWQ de onde calculamos,
Q K
x
XQ
HQKQK
A maior vantagem do Método de Euler é a sua VLPSOLFLGDGH. Contudo, os
resultados obtidos são de IUDFDSUHFLVmR, a menos que se utilize um passo muito
pequeno, o que torna o processo demasiado lento.
BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBB
$QiOLVH1XPpULFD5RViOLD5RGULJXHVH$QWyQLR3HUHLUD
&DStWXOR±(TXDo}HV'LIHUHQFLDLV2UGLQiULDV
BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBB
¨ 0pWRGRGH(XOHU,PSOtFLWR
x
Nas mesmas condições, consideremos agora o desenvolvimento de Taylor
da função \W±K em torno de W,
x
Tomando apenas os dois primeiros termos e para cada W
WQ, temos,
x
que é a fórmula do 0pWRGRGH(XOHU,PSOtFLWR, bem como a informação de
que o HUUR cometido depende da segunda derivada e é 2K .
¨ 0pWRGRVGH7D\ORUGHRUGHPPDLVHOHYDGD
x
Se considerarmos PDLVWHUPRV no desenvolvimento de Taylor, podemos
conseguir HUURVGHWUXQFDWXUDGHRUGHPPDLVHOHYDGD.
BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBB
$QiOLVH1XPpULFD5RViOLD5RGULJXHVH$QWyQLR3HUHLUD
&DStWXOR±(TXDo}HV'LIHUHQFLDLV2UGLQiULDV
BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBB
x
Por exemplo, considerando WUrVWHUPRV,
x
À partida não temos \¶¶W, mas podemos derivar \¶W.
x
Deste modo se define o 0pWRGRGH7D\ORUGHVHJXQGDRUGHP,
onde,
x
O HUUR cometido depende da terceira derivada e é 2K .
x
De modo análogo se podem definir métodos de Taylor de RUGHPPDLV
HOHYDGD, mas são muito pouco utilizados.
BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBB
$QiOLVH1XPpULFD5RViOLD5RGULJXHVH$QWyQLR3HUHLUD
&DStWXOR±(TXDo}HV'LIHUHQFLDLV2UGLQiULDV
BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBB
Å
$OJXQV 0pWRGRV GH 3DVVR 0~OWLSOR 0XOWLSDVVR
x
x
todos os valores X
X XQ
Nos métodos anteriores, o cálculo de
GHILQLomR:
XQ
dependia apenas de XQ. Contudo,
foram já calculados e podem ser utilizados.
Um PpWRGRdiz-se GHP SDVVRV (P ≥ 1)
se
XQ
depender dos
P
valores
XQP XQ .
¨ 0pWRGRGR3RQWR0pGLR
x
Neste caso, a estratégia consiste em aproximar a GHULYDGD pela GLIHUHQoD
ILQLWDFHQWUDGD,
x
donde se obtém o PpWRGRGR3RQWR0pGLR,
x
\ e não o de X .
Note-se que, à partida temos apenas o valor de X
Este tem de ser calculado por um dos métodos de passo simples.
x
O método é H[SOtFLWR e de SDVVRGXSORpois XQ depende de XQ e
também de IQ
≡ IWQ XQ .
BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBB
$QiOLVH1XPpULFD5RViOLD5RGULJXHVH$QWyQLR3HUHLUD
&DStWXOR±(TXDo}HV'LIHUHQFLDLV2UGLQiULDV
BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBB
¨ 0pWRGRGH6LPSVRQ
x
Partindo da IRUPXODomRLQWHJUDO do PVI,
x
e efectuada a discretização, o integral em cada LQWHUYDORGXSOR [WQ WQ]
pode ser aproximado pela 5HJUDGH6LPSVRQ,
x
donde se obtém o 0pWRGRGH6LPSVRQ,
x
que é um método LPSOtFLWR pois IQ≡ IWQ
pois IQ≡ IWQ XQ e IQ ≡ IWQ XQ.
x
Note-se que, todo o método de P SDVVRVrequer uma inicialização para os
x
x
XQ
e de SDVVRGXSOR
P YDORUHVLQLFLDLV X X XP.
Os métodos anteriores tentam, de algum modo, obter uma aproximação do
LQWHJUDO da função IW\W.
Na seguinte família de métodos, a estratégia consiste não em LQWHJUDU I
mas um SROLQyPLRLQWHUSRODGRU de I.
BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBB
$QiOLVH1XPpULFD5RViOLD5RGULJXHVH$QWyQLR3HUHLUD
&DStWXOR±(TXDo}HV'LIHUHQFLDLV2UGLQiULDV
BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBB
¨ $ IDPtOLDGH0pWRGRVGH$GDPV
x
Também partindo da IRUPXODomRLQWHJUDO do PVI,
x
e da GLVFUHWL]DomR em QyVHTXLGLVWDQWHV
passo K
!,
WQ
W QK, Q ≥ com
x
S nós
distintos e só depois é LQWHJUDGRRSROLQyPLRLQWHUSRODGRU de grau S.
x
Os PpWRGRVGDIDPtOLD$GDPV têm como forma geral,
x
Quando E
em primeiro lugar é efectuada uma LQWHUSRODomRSROLQRPLDO em
, os nós de interpolação são WQS WQ ,
a relação é H[SOtFLWD e os esquemas resultantes
chamam-se 0pWRGRVGH$GDPV%DVKIRUWK.
x
Quando Ez
, os nós de interpolação são WQS WQ ,
a relação é LPSOtFLWD e os esquemas resultantes
chamam-se 0pWRGRVGH$GDPV0RXOWRQ.
BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBB
$QiOLVH1XPpULFD5RViOLD5RGULJXHVH$QWyQLR3HUHLUD
&DStWXOR±(TXDo}HV'LIHUHQFLDLV2UGLQiULDV
BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBB
¨ 0pWRGRVGH$GDPV%DVKIRUWK
x
Têm a forma geral:
x
Dada a equação \
IW\W a estratégia consiste em DSUR[LPDU
IW\W SRUXPSROLQyPLR ΠpW de grau S.
Resta então resolver a equação \
LQWHJUDomRGHXPSROLQyPLR.
x
x
ΠpW, que consiste apenas na
Para S , como o polinómio interpolador de JUDX]HUR
temos o PpWRGRGH(XOHU([SOtFLWR.
Π0WQ = IQ,
Para S , construindo o SROLQyPLRLQWHUSRODGRU Π1W nos GRLVSRQWRV
WQe WQ
e LQWHJUDQGR no intervalo [WQ WQ] , não é difícil deduzir a fórmula
do 0pWRGRGH$GDPV%DVKIRUWKGHSDVVRV,
x
De forma análoga, o 0pWRGRGH$GDPV%DVKIRUWKGHSDVVRV,
x
ou ainda o 0pWRGRGH$GDPV%DVKIRUWKGHSDVVRV,
x
BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBB
$QiOLVH1XPpULFD5RViOLD5RGULJXHVH$QWyQLR3HUHLUD
&DStWXOR±(TXDo}HV'LIHUHQFLDLV2UGLQiULDV
BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBB
>
'HGXomR GD IyUPXOD GR 0pWRGR GH $GDPV%DVKIRUWK GH SDVVRV
x
O SROLQyPLRLQWHUSRODGRU Π1W nos GRLVSRQWRV WQe WQ
x
e LQWHJUDQGR Π1W no intervalo [WQ WQ] ,
BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBB
$QiOLVH1XPpULFD5RViOLD5RGULJXHVH$QWyQLR3HUHLUD
&DStWXOR±(TXDo}HV'LIHUHQFLDLV2UGLQiULDV
BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBB
¨ 0pWRGRVGH$GDPV0RXOWRQ
x
Têm a forma geral:
onde Ez .
x
A estratégia é análoga. Contudo, como a interpolação polinomial inclui o
ponto WQ, estes métodos tornam-se LPSOtFLWRV.
Também por isso (e exceptuando o caso S ) cada método de AdamsMoulton de S SDVVRV resulta de uma interpolação em S SRQWRV.
x
Para S
, como o polinómio interpolador de JUDX]HUR no ponto WQ
IQ, temos o PpWRGRGH(XOHU,PSOtFLWR.
x
Para S , se construirmos o polinómio interpolador nos nós WQ e WQ,
obtemos o PpWRGRGH&UDQN1LFROVRQ.
x
O 0pWRGRGH$GDPV0RXOWRQGHSDVVRV é definido por,
x
e o 0pWRGRGH$GDPV0RXOWRQGHSDVVRV é definido por,
x
e o 0pWRGRGH$GDPV0RXOWRQGHSDVVRV é definido por,
x
é
BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBB
$QiOLVH1XPpULFD5RViOLD5RGULJXHVH$QWyQLR3HUHLUD
&DStWXOR±(TXDo}HV'LIHUHQFLDLV2UGLQiULDV
BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBB
¨ 0pWRGRV%')%DFNZDUG'LIIHUHQWLDWLRQ)RUPXODH
x
Esta classe de métodos segue uma HVWUDWpJLDLQYHUVD da anterior.
Uma aproximação de \¶WQ é obtida por GHULYDomRGLUHFWD do SROLQyPLR
de grau S LQWHUSRODGRU de \WQ nos S nós WQS
x
x
São portanto PpWRGRVLPSOtFLWRV e têm a forma geral:
x
Para S
os FRHILFLHQWHV são dados por,
Portanto, para resolver a equação \ W
Ö
WQ WQ.
0pWRGRVGH$GDPV:
IW\W :
- aproximar IW\W por um polinómio;
- integrar polinómio.
Ö
0pWRGRV%'):
- aproximar \Wpor um polinómio;
- derivar polinómio.
BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBB
$QiOLVH1XPpULFD5RViOLD5RGULJXHVH$QWyQLR3HUHLUD
&DStWXOR±(TXDo}HV'LIHUHQFLDLV2UGLQiULDV
BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBB
Å
$ DERUGDJHP GR WLSR 3UHGLWRU ± &RUUHFWRU
x
x
Estes métodos destinam-se a tirar partido das propriedades dos métodos
implícitos, evitando o problema da recursão que lhes é inerente.
São portanto a FRPELQDomR de um PpWRGRH[SOtFLWR com um PpWRGR
LPSOtFLWR:
Em primeiro lugar um PpWRGRH[SOtFLWR calcula um XQ ,
x
valor aproximado de XQ .
x
x
>
XQ
é usado do ODGRGLUHLWR da expressão de
um PpWRGRLPSOtFLWR, gerando um melhor valor para XQ .
Depois, esse
como por exemplo:
0pWRGR GH $GDPV 3UHGLWRU&RUUHFWRU GH  RUGHP
x
Como SUHGLWRU é usado o 0pWRGRGH$GDPV%DVKIRUWKGH SDVVRV
x
Assim:
x
Como FRUUHFWRU é usado o 0pWRGRGH$GDPV0RXOWRQGH SDVVRV
X é dado;
X e X
são calculados por um método de passo simples;
e para Q BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBB
$QiOLVH1XPpULFD5RViOLD5RGULJXHVH$QWyQLR3HUHLUD
&DStWXOR±(TXDo}HV'LIHUHQFLDLV2UGLQiULDV
BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBB
>
0pWRGR GH $GDPV 3UHGLWRU&RUUHFWRU GH  RUGHP
x
Como SUHGLWRU é usado o 0pWRGRGH$GDPV%DVKIRUWKGH SDVVRV
x
Assim:
x
Como FRUUHFWRU é usado o 0pWRGRGH$GDPV0RXOWRQGH SDVVRV
X é dado;
X , X e X
são calculados por um método de passo simples;
e para Q x
Esta combinação dos dois métodos é geralmente chamada PpWRGRGH$GDPV
%DVKIRUWK0RXOWRQ, tal como no módulo abm.m do MATLAB:
IRUQ 1
3UHGLWRU
) >)))IHYDOI7Q\S@
HQG
\S <QK)>@
&RUUHFWRU
<Q <QK)>@
) IHYDOI7Q<Q
$ >7
<
@
BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBB
$QiOLVH1XPpULFD5RViOLD5RGULJXHVH$QWyQLR3HUHLUD
&DStWXOR±(TXDo}HV'LIHUHQFLDLV2UGLQiULDV
BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBB
x
Seguindo uma abordagem do tipo Preditor – Corrector, várias FRPELQDo}HVGH
PpWRGRVpodem ser estabelecidas, como por exemplo,
O PpWRGR3UHGLWRU±&RUUHFWRU(XOHU±7UDSp]LR onde,
x
x
x
x
XQ
é calculado pelo método de (XOHUH[SOtFLWR
e utilizado pelo método LPSOtFLWRGRWUDSp]LR (Crank-Nicolson)
facilmente se conclui,
que corresponde ao PpWRGRGH+HXQ, por isso também chamado PpWRGR
GH(XOHUPHOKRUDGR.
BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBB
$QiOLVH1XPpULFD5RViOLD5RGULJXHVH$QWyQLR3HUHLUD
&DStWXOR±(TXDo}HV'LIHUHQFLDLV2UGLQiULDV
BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBB
Å
2V 0pWRGRV GH 5XQJH.XWWD 5.
x
Retomemos os métodos de XPVySDVVRe H[SOtFLWRV.
x
Mas, métodos de ordem mais elevada requerem o FiOFXORGHPDLVGHULYDGDV
(mais termos da série de Taylor).
x
x
x
>
Por exemplo o método de (XOHUH[SOtFLWR é muito simples, mas também muito
pouco preciso. Para aumentar a precisão, ou GLPLQXtPRVDDPSOLWXGH do passo
ou usamos métodos de RUGHPPDLVHOHYDGD.
C. Runge e M.W. Kutta tentaram uma abordagem diferente.
Consideremos um FDVRSDUWLFXODU ...
5.
x
Pretendemos resolver:
x
Comecemos por calcular,
Como \
\
IW\W
\W \
.
IWQ \Q
IW\W, o valor de . é o GHFOLYH ( da tangente à curva )
em WQ, tal como no método de (XOHUH[SOtFLWR.
BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBB
$QiOLVH1XPpULFD5RViOLD5RGULJXHVH$QWyQLR3HUHLUD
&DStWXOR±(TXDo}HV'LIHUHQFLDLV2UGLQiULDV
BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBB
x
Calculemos agora,
.
IWQ òK\Q òK.
Neste caso . é o GHFOLYH no SRQWRPpGLR do intervalo, tal como no
PpWRGRGRSRQWRPpGLR, mas onde . foi utilizado para determinar o
valor de \ em WQ òK.
x
Sendo . uma aproximação melhor que ., porque não continuar?
x
Calculemos então também:
.
IWQ òK\Q òK.
Agora . é o GHFOLYH no SRQWRPpGLR do intervalo, mas onde . foi
utilizado para determinar o valor de \ em WQ x
E ainda,
.
òK.
IWQ K\Q K.
onde . é o GHFOLYH no H[WUHPRGLUHLWR do intervalo WQ com . utilizado para determinar o respectivo valor de \.
K,
BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBB
$QiOLVH1XPpULFD5RViOLD5RGULJXHVH$QWyQLR3HUHLUD
&DStWXOR±(TXDo}HV'LIHUHQFLDLV2UGLQiULDV
BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBB
x
Por fim, calculamos uma PpGLDGRVGHFOLYHV, mas uma PpGLDSHVDGD
de modo a favorecer os valores interiores.
GHFOLYH . . . . x
Com este valor para o GHFOLYH podemos estabelecer a relação,
que define o método de PpWRGRGH5XQJH.XWWDGHRUGHP,
também chamado 2 0pWRGRGH5XQJH.XWWD,
onde,
x
Como mnemónica das constantes envolvidas nas fórmulas, costuma
utilizar-se uma WDEHOD,
0
1/2 1/2
1/2
0
1/2
1
0
0
1
1/6 1/3 1/3 1/6
BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBB
$QiOLVH1XPpULFD5RViOLD5RGULJXHVH$QWyQLR3HUHLUD
&DStWXOR±(TXDo}HV'LIHUHQFLDLV2UGLQiULDV
BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBB
x
\
Vejamos por H[HPSOR o PVI,
e tentemos obter o valor de
x
\
\
\ ¼
com
K .
. = IWQ \Q = IW \ = 2 . ¼ = ½
declive da UHFWDD]XO em ¼
que encontra o ponto (
x
½, ¾ ).
. = IWQ òK\Q òK.
= I òóòò
=2.½ =
declive da UHFWDYHUGH em ¼
que encontra o ponto (
x
½, ).
. = IWQ òK\Q òK.
= Iòóò= declive da UHFWDODUDQMD em ¼
que encontra o ponto (
x
½, ).
. = IWQ K\Q K.
= Iòó= declive da UHFWDSUHWD em ¼
que encontra o ponto (
, ).
BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBB
$QiOLVH1XPpULFD5RViOLD5RGULJXHVH$QWyQLR3HUHLUD
&DStWXOR±(TXDo}HV'LIHUHQFLDLV2UGLQiULDV
BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBB
x
x
Calculando a PpGLDSHVDGD dos quatro declives,
. . . . e substituindo na UHODomR,
XQ
XQ K . . . . H x
Como o valor exacto é
x
Prova-se que o 5. é 2K .
x
efectuado apenas XPVySDVVRde amplitude K
aproximação obtida é bastante boa.
, concluímos que a
e considerando que foi
Através do exemplo anterior, podemos ainda verificar que o mesmo
resultado \ pode ser interpretado como a PpGLDSHVDGD
dos sucessivos YDORUHVLQWHUPpGLRVGH\ calculados,
\ \ \ \ BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBB
$QiOLVH1XPpULFD5RViOLD5RGULJXHVH$QWyQLR3HUHLUD
&DStWXOR±(TXDo}HV'LIHUHQFLDLV2UGLQiULDV
BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBB
>
$OJRULWPR 5. SDUD FDOFXODU \E FRP Q SDVVRV
^ (QWUDGDIW\DE\ \DQ`
h = b-a / n
t=a
y = y0
para i de 1 até n fazer
k1 = f(t, y)
k2 = f(t + 0.5 h, y + 0.5 h k1)
k3 = f(t + 0.5 h, y + 0.5 h k2)
k4 = f(t + h, y + h k3)
y = y + h (k1 + 2 k2 + 2 k3 + k4) / 6
t=t+h
fimpara
^ 6DtGD\ \E`
BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBB
$QiOLVH1XPpULFD5RViOLD5RGULJXHVH$QWyQLR3HUHLUD
&DStWXOR±(TXDo}HV'LIHUHQFLDLV2UGLQiULDV
BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBB
Å
)RUPD *HUDO GRV 0pWRGRV GH 5XQJH.XWWD
x
Vimos o caso do método de Runge-Kutta de SDVVRV, que tem 4 etapas
(ou estágios) e é H[SOtFLWR. Contudo, os métodos desta classe podem ter
um número diferente de etapas e ser explícitos, implícitos ou adaptativos.
x
8PPpWRGRGH5XQJH.XWWD tem a forma,
onde a IXQomRLQFUHPHQWR é definida por,
e com,
onde
x
V
indica o Q~PHURGHHWDSDV do método específico.
&DGDPpWRGR de Runge-Kutta é completamente caracterizado pelos valores dos
FRHILFLHQWHV ^DLM` , ^EL` e ^FL`.
BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBB
$QiOLVH1XPpULFD5RViOLD5RGULJXHVH$QWyQLR3HUHLUD
&DStWXOR±(TXDo}HV'LIHUHQFLDLV2UGLQiULDV
BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBB
x
x
Esses FRHILFLHQWHV são geralmente apresentados numa tabela chamada
4XDGURGH%XWFKHU.
Vamos considerar apenas os métodos onde,
tal como no caso do exemplo anterior,
0
1/2 1/2
1/2
0
1/2
1
0
0
1
1/6 1/3 1/3 1/6
x
Quando os coeficientes DLM são QXORV para
em função dos .
M ≥ L , cada .L
.L anteriores e o método é H[SOtFLWR.
Caso contrário, o método é LPSOtFLWR e o cálculo dos
um sistema não-linear.
.L
pode ser calculado
exige a resolução de
Também existem esquemas DGDSWDWLYRV, do tipo preditor-corrector.
BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBB
$QiOLVH1XPpULFD5RViOLD5RGULJXHVH$QWyQLR3HUHLUD
&DStWXOR±(TXDo}HV'LIHUHQFLDLV2UGLQiULDV
BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBB
¨ 0pWRGRV GH 5XQJH.XWWD GH GXDV HWDSDV V
x
Consideremos um método de Runge-Kutta com V
solução exacta de partida.
, H[SOtFLWR e seja \Q uma
Assim,
onde,
D F
DD
x
Como
x
Desenvolvendo . em série de Taylor,
x
Então,
e
temos
D F .
BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBB
$QiOLVH1XPpULFD5RViOLD5RGULJXHVH$QWyQLR3HUHLUD
&DStWXOR±(TXDo}HV'LIHUHQFLDLV2UGLQiULDV
BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBB
x
Por outro lado,
x
Donde podemos inferir que,
x
Temos assim uma infinidade de soluções E , E , F e portanto uma LQILQLGDGH
GHPpWRGRVGH5XQJH.XWWDGHHWDSDV.
BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBB
$QiOLVH1XPpULFD5RViOLD5RGULJXHVH$QWyQLR3HUHLUD
&DStWXOR±(TXDo}HV'LIHUHQFLDLV2UGLQiULDV
BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBB
x
Os mais utilizados são:
>
2 PpWRGR GH (XOHU 0RGLILFDGR
>
2 PpWRGR GR 3RQWR 0pGLR
¨ 0pWRGRV GH 5XQJH.XWWD GH WUrV HWDSDV V
x
De forma análoga se pode estabelecer,
x
em função de valores estabelecidos para os coeficientes,
BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBB
$QiOLVH1XPpULFD5RViOLD5RGULJXHVH$QWyQLR3HUHLUD
&DStWXOR±(TXDo}HV'LIHUHQFLDLV2UGLQiULDV
BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBB
¨ 0pWRGRV GH 5XQJH.XWWD GH TXDWUR HWDSDV V
x
Do mesmo modo,
x
com,
x
sendo 5. o mais utilizado, por isso chamado 2 0pWRGRGH5XQJH.XWWD,
BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBB
$QiOLVH1XPpULFD5RViOLD5RGULJXHVH$QWyQLR3HUHLUD