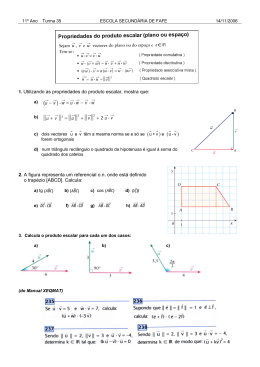
▼
Questão 39
O cubo de vértices ABCDEFGH, indicado na figura, tem arestas de comprimento a. Sabendo-se que M é o
—
ponto médio da aresta AE, então a distância do ponto M ao centro do quadrado ABCD é igual a
H
F
E
M
G
C
D
B
A
a)
a 3
5
d) a 3
b)
a 3
3
e) 2a 3
c)
a 3
2
Resolução
Do enunciado, temos a figura, em que O é o centro do quadrado ABCD:
H
E
a/2
M
a/2
A
G
F
D
C
O
B
—
a 2
Como O é ponto médio da diagonal AC de um quadrado cujos lados medem a, então AO =
.
2
Aplicando o teorema de Pitágoras ao triângulo retângulo AOM, temos:
(OM)2 = (AM)2 + (AO)2
2
 a 2  a 2 
 ∴ OM = a 3
(OM) =   + 


2
2
2
 


2
Resposta: c
1