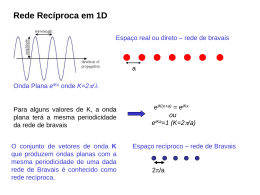
REDE RECÍPROCA
definição
G  m1b1  m2b2  m3b3 ,
b1  2
a 2  a3
a1  (a 2  a 3 )
b 2  2
a 3  a1
a1  (a 2  a 3 )
b 3  2
a1  a 2
a1  (a 2  a 3 )
(mi  Z )
1) a rede recíproca é
uma rede de Bravais
em 2d, a3  z
bi a j  2  i, j
G  R  2 k ,
(k  Z )
 a rede recíproca de uma rede recíproca é a rede direta
2) a rede recíproca não depende da escolha dos
vetores primitivos da rede direta.
3) cada vetor G é ortogonal a uma família de planos
da rede direta (os sítios desses planos têm RG=2k).
d
d |G| = 2 (nesse caso)
4) a rede recíproca tem as mesmas simetrias
pontuais da rede direta.
índices de Miller para planos
• coordenadas do menor G ortogonal à família de
planos. (hkl)
• depende da especificação dos vetores base ai.
• por convenção, nos casos FCC e BCC (que não
têm uma base padrão) se usa uma célula cúbica
convencional.
• nos casos cúbicos se pressupõem a base
cartesiana natural (nos outros sistemas a base ai tem que
ser especificada)
• planos equivalentes usam o símbolo {hkl}
direções cristalinas
• os pontos na forma
R=k (n1a1+n2a2+n3a3)
definem a direção [n1n2n3] (se usam os menores ni
possíveis)
• direções equivalentes usam o símbolo n1n2n3
Espalhamento de raios-X
amostra cristalina vs. policristalina
Alumínio
um programa de análise de dados
de espalhamento