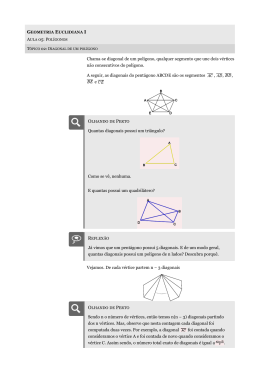
Matemática – 10.º Ano
Escola Secundária de José Falcão
Actividade n.º 4
Data:
Set-2006
MÓDULO INICIAL
Contagens em Poliedros
Objectivos: Utilizar raciocínios combinatórios para determinar invariantes dos sólidos.
No âmbito do ano mundial da matemática – 2000, foi
construído um poliedro regular gigante que se encontra no
pátio de uma escola e que está representado na figura.
1. De que poliedro se trata? Descreve-o.
2. Quantas diagonais terá?
3. Usando as estratégias de contagem completa o quadro:
Quadro
Tetraedro
Cubo
Octaedro
Dodecaedro
Icosaedro
N.º de Faces
N.º de Vértices
N.º de Arestas
N.º total de segmentos
N.º de Diagonais faciais
N.º de Diagonais espaciais
Estratégia de contagem
Para obteres o número de vértices, começa por registar o número de faces do
poliedro, o número de vértices de cada face e ainda o número de faces por vértice.
Para obteres o número de arestas, recorre à fórmula de Euler ou calcula-o a partir do
número de arestas de cada face e tem em conta que cada aresta é comum a duas
faces.
Podes agora obter o número total de segmentos (segmentos de recta que unem
vértices do poliedro), pois de cada vértice podem sair segmentos para todos os outros
vértices. Como deste modo cada segmento é contado duas vezes, o número obtido
tem de ser dividido por dois.
Para obter o número de diagonais faciais tem em conta o número de diagonais de
cada uma das faces.
O número de diagonais espaciais pode obter-se sabendo que:
N.º total de segmentos = N.º de arestas + N.º de diagonais faciais + N.º de diagonais espaciais
Grupo de estágio de matemática
2006-07
Actividade n.º 4
pág. 1 de 1