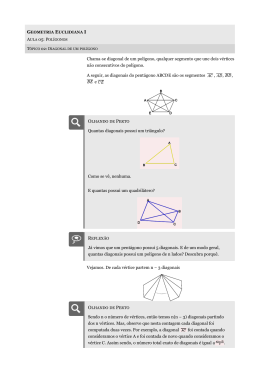
XVI ENDIPE - Encontro Nacional de Didática e Práticas de Ensino - UNICAMP - Campinas - 2012
APRENDIZAGEM EM MATEMÁTICA: CONCEPÇÃO, PROPOSTA E
EXPERIÊNCIA EM UM CURSO DE PEDAGOGIA
Marcelo Dias Pereira
Universidade Municipal de São Caetano do Sul
RESUMO
A formação de professores é um dos temas de grande interesse para a área de Educação.
Os estudos relacionados à aprendizagem foram essenciais para algumas análises sobre
as relações entre concepções e/ou crenças dos professores e sua prática pedagógica,
sobretudo na década de 1990, e continuam sendo relevantes para as atuais análises
relacionadas aos conhecimentos profissionais necessários, aos professores, para
lecionar. Os principais objetivos deste artigo são (I) abordar a concepção de
aprendizagem em Matemática do Educador Matemático italiano Bruno D’Amore, o
qual apóia seu trabalho, dentre outros, em Raymond Duval, autor da Teoria dos
Registros de Representações Semióticas, e (II) relatar uma experiência vivida por nós,
em 2010, em um terceiro ano do Curso de Pedagogia, experiência essa, parte de uma
das atividades relacionadas ao Grupo de Pesquisa formado pelos docentes do Curso de
Pedagogia da Universidade em que atuamos, que tem como uma de suas linhas de
pesquisa a formação, metodologias e práticas de ensino de professores para a Educação
Infantil e anos iniciais do Ensino Fundamental. De acordo com D’Amore a
aprendizagem em Matemática não se constitui apenas da aquisição de conceitos, mas
sim: do saber fazer, que engloba a construção e o uso de conceitos; da aprendizagem de
estratégias, como o saber resolver e o saber demonstrar; e da aprendizagem das
atividades algorítmicas, como o saber calcular e o saber operar. Conclui-se,
parcialmente, que tal concepção, mesmo tendo como uma de suas bases o objetivo do
ensino da Matemática para alunos da Educação Básica, é possível de ser trabalhada com
alunos do Ensino Superior em Pedagogia, em formação inicial.
Palavras-chave: Aprendizagem. Concepção. Registros. Matemática.
Introdução
O que compõe a aprendizagem em Matemática?
São perguntas como essa que nos levam a pesquisar e a experimentar possíveis
respostas, discutindo seus resultados práticos com os próprios alunos participantes
dessas atividades.
Desde 2009, ocasião em que, pela primeira vez, a convite da gestora do Curso de
Pedagogia da Universidade em que lecionamos, assumimos as aulas de Metodologia e
Prática do Ensino de Matemática daquele curso e experimentamos respostas propostas
por Educadores Matemáticos renomados, para essa e outras perguntas. Até então, nossas
Junqueira&Marin Editores
Livro 2 - p.001532
XVI ENDIPE - Encontro Nacional de Didática e Práticas de Ensino - UNICAMP - Campinas - 2012
2
experimentações estavam restritas a um Curso de Licenciatura em Matemática de outra
instituição (de 1998 a 2011) e a cursos de formação em serviço de professores de
Matemática promovidos pelo Governo do Estado de São Paulo (2003).
Além dos resultados práticos discutidos com os participantes das atividades
experimentais (futuros professores), temos contribuído com pesquisas relacionadas à
formação de profissionais da educação e práticas educativas, na linha de pesquisa de
formação, metodologias e práticas de ensino de professores para a Educação Infantil e
anos iniciais do Ensino Fundamental, do Grupo de Pesquisa formado por docentes do
Curso de Pedagogia da Universidade em que atuamos.
Os objetivos deste artigo são abordar uma possível resposta para a pergunta
apresentada e relatar uma experiência, com base na resposta abordada, realizada com
alunos de um terceiro ano do Curso de Pedagogia que lecionamos, relacionada ao
ensino e aprendizagem de um conteúdo geométrico.
Além disso, é também objetivo, a partir da experiência relatada neste artigo,
apresentar uma proposta metodológica para ser trabalhada com futuros professores de
Matemática ou que terão essa disciplina como uma das que lecionará na Educação
Infantil e anos iniciais do Ensino Fundamental.
Ressaltamos que a concepção de aprendizagem que é abordada neste artigo pode
ser utilizada em Ciências e outras disciplinas que utilizam a Matemática como
ferramenta, ou pode ser reformulada para as demais disciplinas de metodologia e prática
de áreas/conteúdos que são objetos de trabalho de futuros docentes.
Aprendizagem em Matemática: a experiência apoiada em uma concepção
Bruno D’Amore, Educador Matemático italiano, defende que a aprendizagem
em Matemática não é composta apenas pela aquisição de conceitos, mas sim: pelo saber
fazer, que engloba a construção e o uso de conceitos; pela aprendizagem de estratégias,
como o saber resolver e o saber demonstrar; e pela aprendizagem das atividades
algorítmicas, como o saber calcular e o saber operar. (D’AMORE, 2005, p. 66-7)
Tendo como base a Teoria dos Registros de Representação Semiótica, de
Raymond Duval, D’Amore (2005), citando trecho da obra Pensamento e Linguagem, de
Vygotsky, afirma que:
... aprender parece ser uma construção submetida à necessidade de
“socializar”, o que acontece obviamente graças a um meio de
comunicação (que pode ser a linguagem) e que na Matemática, de
maneira cada vez mais decisiva, será condicionada pela escolha do
mediador simbólico, isto é, do registro de representação escolhido (ou
Junqueira&Marin Editores
Livro 2 - p.001533
XVI ENDIPE - Encontro Nacional de Didática e Práticas de Ensino - UNICAMP - Campinas - 2012
3
imposto, mesmo que seja apenas pelas circunstâncias). (D’AMORE,
2005, p. 57, grifos do autor)
E sobre construção, especialmente do conhecimento matemático, D’Amore
(2005, p. 63) afirma que ela corresponde à união de três ações: “a capacidade de
representar os conceitos, de tratar as representações obtidas no registro estabelecido e
converter as representações num registro para outro”.
Talvez possa o leitor questionar-se o que significa “converter as representações
num registro para outro”?
Duval (2003, p. 16), abordando sua Teoria, indica existirem dois tipos de
transformações de representações semiótica: o Tratamento que são as “transformações
de representações dentro de um mesmo registro” e a Conversão que são as
“transformações de representações que consistem em mudar de registro, conservando os
mesmos objetos denotados”.
De certa forma, o autor identifica que a Conversão não chama atenção dos
docentes, pois, na maioria das vezes, ela é utilizada por eles para fazer a escolha do
melhor registro para desenvolver o seu plano de ensino e, uma vez desenvolvido, os
docentes apenas utilizam o Tratamento com seus alunos. Um exemplo desse fato, em
Matemática, é a resolução de sistemas lineares: na maior parte das vezes, apenas o
registro algébrico é utilizado para ensinar os alunos a resolvê-los. “Ensinam-se”
procedimentos diferenciados, como adição, substituição e comparação, todos no mesmo
registro, para determinar, caso exista, o par ordenado que satisfaça, ao mesmo tempo,
todas as equações do sistema, mas, dificilmente, converte-se o objeto – resolução de
sistemas lineares – para a representação geométrica, em que cada equação do sistema
representa uma reta e a solução deste é a intersecção de todas essas retas. Aliás, nesse
quadro geométrico há maior riqueza para discussões, pois se podem discutir as possíveis
posições dessas retas e associá-las às possíveis soluções – um único par ordenado,
infinitos pares ordenados ou nenhum par ordenado.
Na concepção de Duval (2003), a maior parte dos problemas relacionados à
aprendizagem em Matemática está relacionada a utilização, apenas, do Tratamento, o
qual, na maioria das vezes, somente oferece condições de apresentar aos alunos o que
lhes serão, eventualmente, úteis muito mais tarde, configurando naquelas famosas
perguntas: pra que serve isso? Onde usaremos isso?
Por esse motivo, D’Amore (2005) adverte para a existência de três ações
constituintes da construção do conhecimento matemático: (1ª) a capacidade de
Junqueira&Marin Editores
Livro 2 - p.001534
XVI ENDIPE - Encontro Nacional de Didática e Práticas de Ensino - UNICAMP - Campinas - 2012
4
representar os conceitos; (2ª) de tratar as representações obtidas no registro estabelecido
(Tratamento); e (3ª) de converter as representações de um registro para outro
(Conversão).
Cabe, para finalizar esse momento, explicitar qual o objetivo do ensino da
Matemática, para Duval, autor de um dos referenciais de D’Amore (2005), na formação
dos alunos, do qual também compartilhamos:
... o objetivo do ensino da matemática, em formação inicial, não é nem
formar futuros matemáticos, nem dar aos alunos instrumentos que só
lhes serão eventualmente úteis muito mais tarde, e sim contribuir para
o desenvolvimento geral de suas capacidades de raciocínio, de análise
e de visualização.” (DUVAL, 2003, p. 11)
Sintetizando, para D’Amore (2005), a construção dos conhecimentos
matemáticos pelo aluno, que ocorre por meio de três ações, é a base para a
aprendizagem em Matemática, que se constitui também de três ações. Todas essas ações
envolvem registros, nos quais os alunos representam o que compreendem e efetuam,
controlando, eles mesmos, as diversidades dos processos matemáticos propostos em
situação de ensino, configurando o que Duval (2003, p. 12) indica ser os elementos
essenciais de investigação do professor em serviço, na tentativa de descrever o
funcionamento cognitivo do aluno: a “originalidade da abordagem cognitiva” de ensino.
Desta forma, o professor poderá intervir, por meio de novas situações de ensino, com o
objetivo de proporcionar aprendizagens ao aluno.
Utilizando essa concepção de aprendizagem em Matemática, de D’Amore
(2005), no segundo semestre de 2010, após abordarmos, em aulas anteriores, os
conceitos de ângulo plano, de polígonos, de polígonos convexos e não convexos, a
definição de diagonais em polígonos, entre outros, propusemos, em certa aula, que os
alunos do terceiro ano de um Curso de Pedagogia tentassem generalizar o número de
diagonais em polígonos convexos, por meio de uma atividade de construção e contagem
das diagonais de vários polígonos convexos.
Como um dos nossos objetivos era identificar, também, os conhecimentos que os
alunos traziam a sobre o número de diagonais em polígonos, nada havia sido comentado
nas aulas anteriores a respeito desse assunto.
No dia da experimentação, foram entregues, aos alunos, folhas com
representações de triângulos (um retângulo, outro acutângulo e outro obtusângulo), de 6
quadriláteros (dentre eles, um retângulo, um quadrado, um losango, um paralelogramo e
um trapézio), de pentágonos, de hexágonos, de octógonos, de eneágonos, de decágonos
Junqueira&Marin Editores
Livro 2 - p.001535
XVI ENDIPE - Encontro Nacional de Didática e Práticas de Ensino - UNICAMP - Campinas - 2012
5
(todos esses com um exemplar regular e outro não regular) e 2 heptágonos, totalizando,
21 polígonos convexos representados, os quais, na nossa opinião, são mais acessíveis à
construção, à visualização e à contagem das diagonais, quando possuem.
Foi solicitado aos alunos que formassem grupos de 5 integrantes, no máximo, e,
após a formação do grupos, as únicas instruções colocadas na lousa foram:
Os polígonos representados nas folhas são convexos, conforme já estudamos.
(1) Construir (com o auxílio de uma régua) e contar todas as diagonais desses
polígonos, iniciando pelos triângulos, depois dos quadriláteros, e assim por
diante em ordem crescente de número de lados, e registrar as conclusões sobre
os números de diagonais de todos os triângulos, de todos os quadriláteros, de
todos os pentágonos, e assim por diante.
(2) Conferir as conclusões quanto aos números de diagonais com os demais
grupos.
(3) Responder as questões:
I)
Quantas diagonais existem em um dodecágono convexo?
II)
Quantas diagonais existem em um icoságono convexo?
III)
Quantas diagonais existem em um polígono convexo com n
lados?
Os objetivos específicos das atividades relacionadas ao item (1) eram:
(a) verificar se os alunos haviam compreendido a definição de diagonais em
polígonos. Na aula anterior tínhamos visto que as diagonais dos polígonos eram os
segmentos de reta com extremidades em dois vértices não consecutivos desse polígono;
(b) levar os alunos a concluírem que o número de diagonais, em polígonos com a
mesma quantidade de lados, é sempre o mesmo.
(c) fazer com que os alunos obtivessem, por traçados e contagens, ou outro
procedimento, o número de diagonais de polígonos convexos, até 10 lados.
Já o objetivo geral do item (1) estava relacionado ao saber fazer da concepção
sobre aprendizagem Matemática de D’Amore (2005), uma vez que os alunos deveriam
utilizar conceitos e definições já estudadas para construir um novo conceito: polígonos
com a mesma quantidade de lados têm o mesmo número de diagonais.
Na atividade relacionada ao item (2) o objetivo específico era o de, apenas, levar
os alunos a constatarem se as conclusões obtidas no item (1) estavam de acordo com as
dos demais grupos. Em se tratando do objetivo geral, os alunos deveriam socializar os
Junqueira&Marin Editores
Livro 2 - p.001536
XVI ENDIPE - Encontro Nacional de Didática e Práticas de Ensino - UNICAMP - Campinas - 2012
6
resultados obtidos com membros dos demais grupos, possibilitando novas reflexões, se
fosse o caso.
Quanto às atividades relacionadas ao item (3), seus objetivos específicos eram:
(d) verificar se os alunos, através das atividades relacionadas ao item (1),
encontrariam uma regularidade para calcular o número de diagonais e, assim, responder
as perguntas (I) e (II);
(e) verificar se os alunos generalizariam o número de diagonais em um polígono.
Já o objetivo geral das atividades do item (3) era a aprendizagem de estratégias e
de atividades algorítmicas e isso somente seria possível se houvesse a Conversão do
registro geométrico para o registro algébrico, dada a dificuldade de traçar e contar todas
as diagonais, principalmente de um icoságono, que tem 20 lados.
Observando os nove grupos formados, verificamos que os alunos que não
haviam compreendido a definição de diagonais em polígonos da aula anterior, foram
rapidamente instruídos pelos colegas que haviam entendido aquela definição e a
compreenderam.
Quanto aos objetivos (b) e (c), observamos que todos os grupos chegaram aos
números corretos de diagonais e concluíram que todos os quadriláteros têm o mesmo
número de diagonais, que todos os pentágonos têm o mesmo número de diagonais, e
assim por diante. Observamos também que, para se chegar a essa conclusão, apenas 3
grupos não construíram todas as diagonais de todos os exemplares de polígonos.
Questionados os 3 grupos sobre como responderam ao item (1), um deles, que
chamaremos de α, respondeu que utilizaram a expressão
(n − 3).n , obtida através de um
2
notebook de um dos seus componentes, conectado a internet.
Os outros dois grupos, que estavam um ao lado do outro e os chamaremos de β,
justificaram as respostas da seguinte forma: “se os polígonos possuem o mesmo número
de lados, então é claro que possuem o mesmo número de diagonais, pois isso aconteceu
com os triângulos, com os quadriláteros e com os pentágonos.”
Não é uma justificativa plausível que possa ser utilizada como comprovação de
tal fato, mas lendo rapidamente as resoluções enquanto eles se justificavam, observamos
que, intuitivamente, eles utilizaram a seguinte ideia: nos hexágonos, para cada vértice,
eles contaram 3 diagonais e perceberam que todas elas eram contadas duas vezes. Logo,
eram, ao todo, 6 × 3 ÷ 2 , ou seja, 9 diagonais, qualquer que fosse o hexágono; para os
Junqueira&Marin Editores
Livro 2 - p.001537
XVI ENDIPE - Encontro Nacional de Didática e Práticas de Ensino - UNICAMP - Campinas - 2012
7
heptágonos, eles contaram 4 diagonais para cada vértice, que também eram em dobro
contadas. Logo, eram, ao todo, 7 × 4 ÷ 2 diagonais; e assim por diante, até o decágono.
Percebemos, então, que nesses grupos ocorrera a Conversão de registros logo nas
atividades do item (1) e que essa ideia poderia levá-los à solução das perguntas (I) e (II)
mais facilmente.
Observando as estratégias utilizadas pelos grupos para responder à questão (I),
verificamos que três, dos nove grupos, construíram um dodecágono convexo e traçaram
suas diagonais; quatro grupos utilizaram a expressão
(n − 3).n , obtida via internet pelo
2
grupo α; e dois, dos nove grupos, o β, resolveram, não diretamente pela expressão
(n − 3).n , mas da seguinte forma: multiplicaram 12 por 9 e dividiram o resultado por 2.
2
Questionados por que 12 × 9 ÷ 2 , eles responderam: “12 porque são 12 vértices em um
dodecágono; 9 porque são 9 diagonais por vértice; e 2 porque observamos que,
multiplicando 12 por 9, as diagonais são contadas duas vezes.”
Não satisfeito, perguntamos: por que 9 diagonais por vértice? A resposta dada
foi: “porque com os 12 vértices, não podemos contar 3 segmentos como diagonal:
aquele com uma extremidade no vértice da frente, outro com uma extremidade no
vértice de trás [estavam referindo-se aos vértices consecutivos] e o outro com
extremidade nele mesmo [referindo-se que não havia como construir um segmento de
reta tendo um único ponto como extremidades]”.
Com relação à questão (II), percebendo o trabalho que daria para construir e
contar todas as diagonais de um icoságono, sete dos nove grupos utilizaram a expressão
(n − 3).n , obtida na internet pelo grupo α. Dessa forma, o objetivo (d) não fora atingido
2
pela maioria dos alunos e o objetivo (e) já não fazia mais sentido para esses sete grupos.
Esperando dos grupos β uma resolução idêntica à da questão anterior, fomos
surpreendidos: eles responderam corretamente 170 diagonais, mas apresentaram a
seguinte resolução:
17 + 17 + 16 + 15 + 14 + 13 + 12 + 11 + 10 + 9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1 = 170
Curiosos para entender a resolução, questionamos os grupos β sobre o porquê
daquela resolução. Em resposta, disseram: “nós descobrimos, pelos casos anteriores,
uma coisa interessante e que deu certo”. Nesse momento, a maioria dos demais alunos
Junqueira&Marin Editores
Livro 2 - p.001538
XVI ENDIPE - Encontro Nacional de Didática e Práticas de Ensino - UNICAMP - Campinas - 2012
8
também começou a interessar-se pela explicação dos colegas e um dos alunos dos
grupos β, a nosso pedido, passou a mostrar na lousa o que eles haviam descoberto para
um quadrilátero, um heptágono e um decágono.
Para o quadrilátero, apresentou a operação: 1 + 1 = 2 , justificando-a da seguinte
maneira: “são 4 vértices: A, B, C e D. Pelo vértice A podemos construir apenas uma
diagonal, pelo vértice B, podemos construir apenas outra, pelos vértices C e D, podemos
construir apenas uma diagonal para cada vértice, mas elas já foram contadas. Então
temos 1 + 1 = 2 diagonais.”
Para o heptágono, começou justificando: “são 7 vértices: A, B, C, D, E, F e G.
Pelo vértice A podemos construir 4 diagonais; pelo vértice B, também 4 diagonais; pelo
vértice C, podemos construir 4 diagonais, mais uma delas já foi contada: a de
extremidades A e C; pelo vértice D, também 4 diagonais, mas duas já foram contadas:
as de extremidades A e D e de extremidades B e D; pelo vértice E, das 4 diagonais
possíveis, três já foram contadas: de extremidades A e E, B e E e C e E; pelos vértices F
e G, todas as diagonais já foram contadas. Sendo assim, temos 4 + 4 + 3 + 2 + 1 = 14
diagonais”.
Explicação semelhante deram para o decágono, ao contarem 35 diagonais como
7 + 7 + 6 + 5 + 4 + 3 + 2 + 1 = 35 , e acrescentaram: “sempre os dois primeiros números
serão os obtidos da quantidade de vértice menos três, pois correspondem ao número de
diagonais que podemos traçar por cada vértice; o menos três é porque quando fixamos
um dos vértices, não podemos contar 3 segmentos como diagonal: aquele com uma
extremidade no vértice da frente, outro com uma extremidade no vértice de trás
[referindo-se, respectivamente, aos vértices posterior e anterior, quando tomados três
vértices consecutivos] e o outro com extremidade nele mesmo.”
Comprovamos, naquele momento, que os grupos β converteram um registro
geométrico para um registro numérico.
Faltava, agora, a generalização, ou seja, a resposta à questão (III), o que,
infelizmente os grupos β não conseguiram apresentar e, tampouco, os demais.
Desta forma, assumimos, então, essa tarefa e, juntamente com os alunos, com
base nas explicações dadas pelo integrante dos grupos β, chegamos à seguinte
conclusão:
o
número
de
diagonais
de
um
polígono
com
n
lados
é
2.(n − 3) + (n − 4) + (n − 5) + ... + 2 + 1 + 0 , em que n representa o número de lados de um
polígono.
Junqueira&Marin Editores
Livro 2 - p.001539
XVI ENDIPE - Encontro Nacional de Didática e Práticas de Ensino - UNICAMP - Campinas - 2012
9
Restava-nos, para aquele momento, a responsabilidade de mostrar para aqueles
alunos do terceiro ano do Curso de Pedagogia de 2010, que a generalização encontrada
naquela situação era equivalente à expressão
(n − 3).n
2
que indica o número de
diagonais de um polígono, obtida na internet. Tarefa que foi cumprida em aula da
semana seguinte.
Considerações finais
Particularmente, mesmo com a “interferência” da internet, acreditamos que a
proposta da atividade apresentada contribuiu para a ocorrência da aprendizagem em
Matemática, na concepção de D’Amore (2005), pois ela proporcionou a alguns alunos o
saber fazer, o saber resolver e o saber demonstrar o que foi efetuado.
Além disso, a capacidade de representar os conceitos, de tratar as representações
obtidas em um registro (neste caso, o registro geométrico – a Transformação), e a
Conversão das representações de um registro para outro (do geométrico para o
numérico), mesmo tendo ocorrido apenas para parte dos alunos, contribuíram para a
construção de novos conhecimentos matemáticos para a turma do terceiro ano de 2010
do Curso de Pedagogia da Instituição em que atuamos, pois puderam ser socializadas e
discutidas com os demais.
Porém, a concepção de aprendizagem em Matemática de D’Amore (2005) está
relacionada a um trabalho que procura discutir, epistemologicamente, a Didática da
Matemática e tem como base uma Teoria utilizada para fundamentar pesquisas na área
da Educação Matemática, mais especificamente, para descrever o funcionamento
cognitivo dos alunos. Trata-se de uma concepção relacionada, ao nosso ponto de vista,
ao estudo cognitivo de atividades matemáticas em alunos da Educação Básica.
Além disso, há um agravante: conforme defendido por Duval (2003, p. 11) e
apresentado neste artigo, o objetivo do ensino da Matemática, na formação inicial
[grifo nosso] é contribuir para o desenvolvimento da capacidade de raciocínio, de
análise e de visualização. Ora, o que podemos entender como formação inicial? Ou
então: alunos de um Curso de Pedagogia, ou outro curso de nível superior, como por
exemplo, de Licenciatura em Matemática, estão em formação inicial no que se refere à
aprendizagem em Matemática?
Acreditamos não haver uma única resposta para essas perguntas. Mas,
acreditamos que a concepção de D’Amore (2005), abordado neste artigo, assim como o
Junqueira&Marin Editores
Livro 2 - p.001540
XVI ENDIPE - Encontro Nacional de Didática e Práticas de Ensino - UNICAMP - Campinas - 2012
10
objetivo do ensino da Matemática, defendido por Duval (2003), podem ser estendidos
para a formação inicial de professores que lecionarão Matemática, pois esses cursos não
têm o objetivo de formar Matemáticos.
Por outro lado, esses cursos não podem ter apenas nessas concepções sua base,
pois não estão lidando com alunos da faixa etária da Educação Básica.
Por esses motivos, deixamos como proposta a concepção de aprendizagem em
Matemática abordada neste artigo.
Concluindo, registramos que não tivemos oportunidade para discutir,
especialmente com essa turma de 2010, a concepção de aprendizagem em Matemática
aqui abordada. Mas temos convicção, pelos relatos sobre as atividades desenvolvidas
durante aquele ano, de que a maioria dos alunos entendeu a importância da Matemática
na sua formação inicial de futuros Pedagogos, assim como a importância da
metodologia e da prática de aulas utilizadas para o ensino dessa disciplina.
Referências bibliográficas:
D’AMORE, Bruno. Epistemologia e Didática da Matemática. São Paulo: Escrituras
Editora, 2005.
DUVAL, Raymond. Registros de Representações Semióticas e funcionamento
cognitivo da compreensão em Matemática. In: MACHADO, Silvia Dias Alcântara
(Org.). Aprendizagem em Matemática: Registros de Representação Semiótica.
Campinas: Papirus, 2003.
Junqueira&Marin Editores
Livro 2 - p.001541