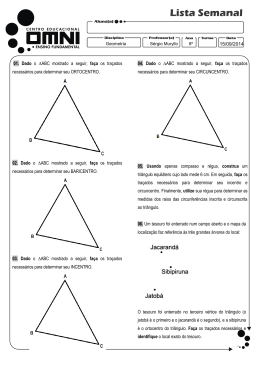
Centro Educacional Olívia Lima.
São Gonçalo, ______ de _____________________________ de 2012.
Professor (a): Suhender Ribeiro
Turma: 8º ano A
Aluno (a): _________________________________
nº: _____
Teste de Matemática – 3º bimestre
INSTRUÇÕES PARA A REALIZAÇÃO DA AVALIAÇÃO
Ao receber sua avaliação observe:
▪Se conferem todas as folhas na sequência de questões.
▪ Se há falhas de impressão ou impressões que não podem ser lidas.
▪ Se você perceber alguma falha, solicite o seu professor que substitua sua prova antes de iniciá-la.
Com a prova em mãos não esqueça:
▪ Concentre-se no que vai fazer, mas sem ansiedade. Não tenha pressa de acabar. Use o tempo disponível.
▪ Complete todos os dados de identificação: nome completo, número e turma.
▪ Leia e releia todas as questões. Inicie resolvendo as mais fácies ou aquelas que você tem certeza das respostas.
▪ Dê atenção e tempo às questões mais difíceis.
▪ Não deixe questões em branco. Você recebeu explicações sobre todos os assuntos. Portanto, recorra a sua memória ou o seu
raciocínio.
▪ Corrija os seus erros de grafia.
▪ Não use corretivos nas questões objetivas.
▪ É obrigatório ter desenvolvimento nas questões que exigem cálculos.
▪ Não rabisque ou desenhe a prova. A prova é um documento.
▪ Faça sua prova sempre de caneta esferográfica AZUL OU PRETA.
▪ Nas questões objetivas (a)s respostas deve(m) ser marcadas com um (X).
1) Enuncie e demonstre a segunda propriedade estudada em sala que relaciona os
ângulos de um triângulo.
2) Utilizando a propriedade enunciada na questão anterior, calcule a medida do ângulo
externo na figura abaixo.
3x–16º
4x+22º
2x+6º
3) Na figura abaixo. Determine os segmentos que representam mediana, bissetriz e
altura, sabendo que
.
A
____________________________
____________________________
____________________________
B

H
N
P
C
4) Na figura,
então x vale:
a)
b)
c)
d)
e)
Ĉ
B̂
. Se D é o incentro do triângulo ABC,
A
40°
120°
130°
150°
100°
D
x
5) No triângulo ABC abaixo,
B
C
é a mediana. Determine o perímetro desse triângulo.
A
3,5 cm
2,5 cm
B
C
M
1,9 cm
6) Determine o valor de x, sabendo que
e
são bissetrizes dos ângulos indicados.
E
D
C
x
20°
B
A
7) Calcule, na figura abaixo, o valor do ângulo interno x.
8)
Na figura, o ABC é congruente ao EDC. Determine o caso de congruência e o valor
de x e y.
15
23
3y + 2
2x – 3
9) Classifique em verdadeiro ou falso as afirmações abaixo:
( ) O encontro das bissetrizes de um triângulo é chamado de incentro.
( ) Baricentro é o encontro das alturas de um triângulo.
( ) Num triângulo acutângulo, o ortocentro aparece no interior da figura.
( ) É possível construir um triângulo de medidas 3 cm, 5 cm e 10 cm.
( ) Num triângulo retângulo, o menor lado é chamado de hipotenusa.
10) Sabendo que
determine quanto vale:
a)
b)
c)
d)
BOA PROVA!