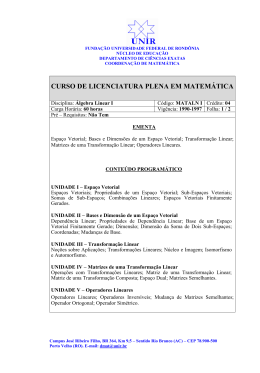
Elementos de
Matemática Avançada
Prof. Dr. Arturo R. Samana
Semestre: 2012.2
Conteúdo
- Objetivos da Disciplina
- Ementa curricular
- Critérios de avaliação
- Conteúdo programático
- Programação
Objetivos da disciplina
Atendendo aos objetivos gerais do curso de
Licenciatura Plena em Física na modalidade à
distância, esta disciplina oferecerá ao aluno
aprender as ferramentas matemáticas necessárias
para a abordagem de certos problemas físicos.
Ementa Curricular
Álgebra linear,
funções de variável complexa;
funções especiais;
transformadas de Fourier e Laplace;
espaços vetoriais de dimensão finita e infinita;
teoria das distribuições e das perturbações.
Critérios de Avaliação
Três (03) Provas Processais (40 %)
Duas (02) Provas Presenciais (60 %)
1 Prova Final
Metodologia de ensino
• Compreensão, interpretação leitura dos textos e
resolução literatura proporcionada pela coordenação
UAB.
• Uso de matemática elementar para problemas não
comuns.
• Uso de matemática não elementar para problemas
físicos comuns.
Conteúdo Programático
UNIDADE 1 - ÁLGEBRA LINEAR – MATRIZES
DEFINIÇÕES PRÉVIAS: Igualdade de Matrizes, Matriz Real
e Complexa, Coluna, Quadrada, Nula, Diagonal, Identidade,
Triangular Superior, Triangular Inferior, Transposta,
Simétrica, Hermitiana.
OPERAÇÕES COM MATRIZES: soma e produto, produto por
escalares.
Submatriz,
Determinante de uma matriz, matriz adjunta e matriz inversa,
propriedades
DETERMINANTE
E
MATRIZ
INVERSA:
Conteúdo Programático
UNIDADE 2 - ÁLGEBRA LINEAR - ESPAÇOS VETORIAIS
ESPAÇOS VETORIAIS DE DIMENSÃO FINITA: Vetores.
Espaços Vetoriais, Combinação Linear, Vetores Linearmente
Independentes e Linearmente Dependentes, Base de um
Espaço Vetorial, Dimensão de um Espaço Vetorial,
Componentes de um Vetor.
ESPAÇOS DE HILBERT: Espaço Vetorial com Produto
Interno ou Espaço de Hilbert,Norma de um Vetor, Distância
em um espaço vetorial com produto interno, Ângulo,Vetores
Ortogonais, Bases Ortogonais e Ortonormais,Subespaços
Vetoriais
Conteúdo Programático
UNIDADE 2 - ÁLGEBRA LINEAR - ESPAÇOS VETORIAIS
TRANSFORMAÇÕES LINEARES:Transformação Linear.
Matriz Associada a uma Transformação Linear, Imagem de
uma Transformação Linear, Núcleo de uma Transformação
Linear
Conteúdo Programático
UNIDADE 3 - ÁLGEBRA LINEAR - OPERADORES
OPERADORES ORTOGONAIS, UNITÁRIOS, SIMÉTRICOS
E HERMITIANOS: Operadores ortogonais e unitários,
Operadores simétricos e hermitianos,
PROBLEMA DE AUTOVALORES E AUTOVETORES:
Autovalores e Autovetores de uma Matriz, Diagonalização de
Matrizes, Autovalores e AutoVetores de um Operador,
Conteúdo Programático
UNIDADE 4 - FUNÇÕES DE VARIÁVEL COMPLEXA
NÚMEROS COMPLEXOS: Geometria e álgebra básica de
números complexos, Fórmula de De Moivre e o Calculo de
Raízes,
FUNÇÕES COMPLEXAS E A FÓRMULA DE EULER: Aplicações
da fórmula de Euler, Funções plurívocas e superfícies de riemann,
funções analíticas.
O TEOREMA DE CAUCHY : Outros teoremas de integrais. a
fórmula da integral de Cauchy .
SEQUÊNCIAS E SÉRIES COMPLEXAS. Séries de taylor e de
laurent. zeros e singularidades.
O TEOREMA DO RESIDUO E SUAS APLICAÇÕES.
Conteúdo Programático
UNIDADE 5 - FUNÇÕES ESPECIAIS
COORDENADAS CILÍNDRICAS E ESFERÍCAS
PROBLEMAS COMUNS DE VALORES DE CONTORNO
O PROBLEMA DE STURM-LIOVILLE
PROBLEMAS DE APLICAÇÃO: Potencial eletroestático no
espaço vazio, Vibração livre de uma membrana circular
Conteúdo Programático
UNIDADE 6 - TEORIA DAS DISTRIBUIÇÔES E DE
PERTURBAÇÔES
FUNÇÕES DE SCHWARTZ E FUNÇÕES DE TESTE.
TRANSFORMADAS DE FOURIER E DISTRIBUIÇÔES:
Aplicações das distribuições às equações diferenciais. Funções
de green
INTRODUÇÃO À TEORIA DE PERTURBAÇÔES.
Sumario
* Critérios de Avaliação:
Três (03) Provas Processais (40 %)
Duas (03) Provas Presenciais (60 %)
1 Prova Final
* Compreensão, interpretação leitura dos textos e
resolução literatura proporcionada pela coordenação
UAB.
UNIDADE 1 - ÁLGEBRA LINEAR – MATRIZES
UNIDADE 2 - ÁLGEBRA LINEAR - ESPAÇOS VETORIAIS
UNIDADE 3 - ÁLGEBRA LINEAR - OPERADORES
UNIDADE 4 - FUNÇÕES DE VARIÁVEL COMPLEXA
UNIDADE 5 - FUNÇÕES ESPECIAIS
UNIDADE 6 - TEORIA DAS DISTRIBUIÇÔES E DE
PERTURBAÇÔES