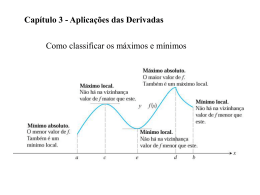
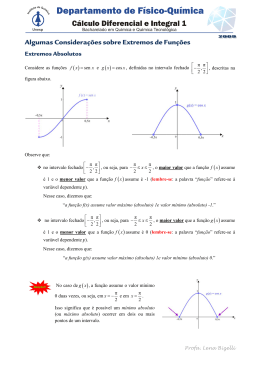
Profª Débora Bastos
Programa
EMENTA
 Aplicações da derivada: determinação de máximos e
mínimos, concavidade e pontos de Inflexão de funções,
esboço do gráfico de funções, problemas de otimização.
 Integração indefinida: método de substituição, integrais de
produtos e potências de funções trigonométricas, método
de integração por partes, método de substituição
trigonométrica, método para integração de funções
racionais.
 Integração definida: definição e cálculo da integral
definida, métodos para calcular integrais definidas,
aplicações da integral definida, cálculo de áreas, volume de
sólidos de revolução, cálculo do comprimento de arco.
Bibliografia
1. LARSON, Roland E.; HOSTETLER, Robert P. e
EDWARDS, Bruce H. Cálculo com Aplicações. Editora
LTC, 4. Ed.
2. HOFFMANN, Laurence D. & BRADLEY, Gerald L.
Cálculo - Um curso moderno e suas aplicações. Editora
LTC, 6. Ed.
3. LEITHOLD, Louis. Cálculo com Geometria Analítica.
São Paulo: Harper & Row do Brasil,1982. (Campus
Cidade)
Avaliação
 Provas:
1º Bimestre: 25/04/2012
2º Bimestre: 27/06/2012
Exame: ?
 Sem Vade Mecum (orientação apenas para os estudos)
 Sem calculadora
 Formulário de derivadas e/ou integrais
1
Atendimento
 Sala 726
 Tel: 3233 8670
 E-mail: [email protected]
 Site: http://pertenceamatematica.pbworks.com
 Horário: ?
Aplicações da Derivada
Estudo do Gráfico de funções.
Poderemos:
 Verificar a existência e encontrar pontos extremos
(máximos e mínimos) e críticos (inflexão);
 Determinar intervalos em que a função é crescente ou
decrescente;
 Determinar intervalos em que a função tem
concavidade para cima ou para baixo;
 Esboçar gráficos sabendo a lei de formação da função.
2
Pontos extremos
y
C
D
A
x
B
 Pontos de máximo relativo (local): A e C.
 Pontos de mínimo relativo (local): B e D.
 Ponto de máximo absoluto: C.
 Ponto de mínimo local: 
3
Definições
 Definição 1: Uma função f tem um
y
máximo local (relativo) em c, se
existir um intervalo aberto I,
contendo c, tal que f(c) > f(x) para
todo x  I.
f(c)
f(x1)
c x1
x
I
y
 Definição 2: Uma função f tem um
f(x1)
f(c)
c x1
I
x
mínimo local (relativo) em c, se
existir um intervalo aberto I,
contendo c, tal que f(c) < f(x) para
todo x  I.
4
Exemplo
 f(x) = 3x4  12x2
x  (  2, 2)
y
2

2
C
2
A  12 B
2
x
Pontos de mínimo local
A  2 ,12
B  2 ,12
Ponto de máximo absoluto
C ( 0, 0)
5
Mais definições
 Definição 3: Dizemos que f(c) é o máximo absoluto da
função f, se c  D(f) e f(c) > f(x) para todo x  D(f).
 Definição 4: Dizemos que f(c) é o mínimo absoluto da
função f, se c  D(f) e f(c) < f(x) para todo x  D(f).
6
7
Interpretação Geométrica da Derivada.
 Por definição f ’(x) =
f ( x  x)  f ( x)
x 0
x
lim
 P é um ponto qualquer da
função.
 s é a reta secante à função
passando por P e Q.
  é o ângulo da secante com
o eixo x.
 tg  = f ( x  x)  f ( x)
x
 O que acontece com a reta s se x  0?
Interpretação geométrica da derivada
f ( x  x)  f ( x)
 tg
x 0
x
 f ’(x) = lim
t
 A derivada da função em
um ponto é a inclinação
(coeficiente angular)
da reta tangente à função
no ponto P.

O que isso tem a ver com os extremos de
uma função?
 Se um ponto for extremo (máximo ou mínimo), como
serão as retas tangentes à função nesses pontos?
 Qual o ângulo entre a reta tangente t e o eixo ox?
 Qual o valor da tangente desse ângulo?
Afinal...
8
 Se P(xp, f(xp)) é um ponto extremo, então f ’(xp) = 0
 Teorema 1: Se f(x) foi definida para todos os valores de x
no intervalo aberto (a,b) e se f tiver um extremo relativo
em c, onde a < c < b, então f ’(c)=0, se f ’(c) existir.
 Exemplo: f(x) = 2x2 – 8x + 6
O vértice é um ponto de mínimo. V(2, 2)
f ’(x) = 4x – 8
f ’(2) = 4.2 – 8 = 0
Se f’(x) = 0 não necessariamente temos P(c, f(c))
um ponto extremo.
 Exemplos: f(x) = (x – 2)3 + 4
 f ’(x) = 3(x – 2)2
 3(x – 2)2 = 0
x=2
 P (2, 4) não é um ponto extremo, nem máximo, nem
mínimo.
9
Pode ocorrer ainda que exista um ponto
10
extremo, mas f’(x)  0.
 Exemplo:
2x  1, se x  3
f ( x)  
8  x, se x  3
 f ’(3) não existe, pois f’+(3)  f’-(3).
Gráficos com “bicos” não são deriváveis nesses pontos.
 Definição 5: Se c  D(f) e se f ’(c) = 0, ou f ’(c) não
existir , então c será chamado de número crítico de f e
P (c, f(c)) ponto crítico de f.
Existência de pontos extremos.
11
 Teorema 2: (Teorema do valor extremo) Se a função f for
contínua no intervalo fechado [a,b], então f terá um valor
máximo absoluto e um valor mínimo absoluto em [a,b].
 Os pontos críticos de uma função que satisfaz o Teorema do
valor extremo podem ser determinados pelo seguinte
processo:
1- Achar os valores da função nos números críticos de f em
(a,b).
2-Ache os valores de f(a) e f(b).
3- O maior dentre os valores das etapas 1 e 2 será o valor
máximo absoluto e o menor será o valor mínimo absoluto.
Exemplo
 Ache os extremos absolutos de f em
1


2
,

2 

se
f(x) = x3 + x2 – x + 1.
Solução: f é uma função polinomial, então é contínua em
lR, logo também é em  2, 1  .
2

Pontos críticos:
f’(x) = 3x2 +2x – 1
f’(x) = 0  x = 1/3 ou x = -1
1


2
,
Ambos estão em  2  .
Cálculo das ordenadas:
X
-2
-1
1/3
½
f(x)
-1
2
22/27
7/8
Resposta: A é mínimo absoluto, B é máximo absoluto, C
é mínimo local e D é máximo local.
Problema de máximo: Um exemplo.
 Um fabricante de caixas de papelão deseja fazer caixas
abertas a partir de pedaços quadrados de papelão com
12 cm de lado, cortando quadrados iguais dos quatro
cantos e dobrando os lados para cima. Queremos
encontrar o comprimento do lado do quadrado a ser
cortado para obter uma caixa com o maior volume
possível.
Solução:
12
Solução
 Volume = área da base x altura
 V(x)= (12-2x)2x
 V(x)= 144x – 48x2 + 4x3
x  [0,6]
V é contínua em [0,6]
Pontos críticos
V’(x) = 144 – 96x + 12x2
V’(x) existe para qualquer valor real.
13
Solução
144 – 96x + 12x2 = 0  x = 2 ou x =6
Ambos pertencem ao intervalo [0,6]
X
0
2
6
V(x)
0
128
0
Ponto de máximo P (2, 128)
Resposta: O volume máximo possível é de 128 cm3,
quando é cortado nos cantos um quadrado de 2 cm de
lado.