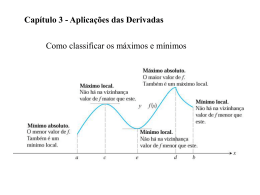
Algumas Considerações sobre Extremos de Funções
Extremos Absolutos
 π π
Considere as funções f  x   sen x e g  x   cos x , definidas no intervalo fechado   ,  , descritas na
 2 2
figura abaixo.
Observe que:
π
π
 π π
 no intervalo fechado   ,  , ou seja, para   x  , o maior valor que a função f  x  assume
2
2
 2 2
é 1 e o menor valor que a função f  x  assume é -1 (lembre-se: a palavra “função” refere-se à
variável dependente y).
Nesse caso, dizemos que:
“a função f(x) assume valor máximo (absoluto) 1e valor mínimo (absoluto) -1.”
π
π
 π π
 no intervalo fechado   ,  , ou seja, para   x  , o maior valor que a função g  x  assume
2
2
 2 2
é 1 e o menor valor que a função f  x  assume é 0 (lembre-se: a palavra “função” refere-se à
variável dependente y).
Nesse caso, dizemos que:
“a função g(x) assume valor máximo (absoluto) 1e valor mínimo (absoluto) 0.”
No caso de g  x  , a função assume o valor mínimo
0 duas vezes, ou seja, em x  
π
π
e em x  .
2
2
Isso significa que é possível um mínimo absoluto
(ou máximo absoluto) ocorrer em dois ou mais
pontos de um intervalo.
Profa. Lena Bizelli
Funções definidas pela mesma regra podem ter extremos diferentes, dependendo do domínio. Para ver esse
fato, considere a função g  x   cos x definida em vários domínios diferentes.
Analisando atentamente as diferentes situações apresentadas acima, podemos concluir que: se uma função
y  f  x  for contínua em um intervalo fechado  a,b  , ela sempre apresentará um mínimo e um máximo
absolutos nesse intervalo.
Profa. Lena Bizelli
Extremos Locais
Agora que você já aprendeu a analisar a existência de máximo e mínimo absolutos, vamos nos concentrar no
problema de localizar máximo e mínimo local de uma função y  f  x  .
Considere o gráfico da função y  f  x  descrito na figura abaixo.
Observe que:
 em uma vizinhança qualquer do ponto P (pontos próximos de P à direita e à esquerda de P) não
existe valor de f (ou de y) maior do que 10. Quando isso acontece, dizemos que a função y  f  x 
apresenta um máximo local em P.
Em outras palavras, em x = 2 existe um ponto de máximo local da função y  f  x  .
 em uma vizinhança qualquer do ponto Q (pontos próximos de Q à direita e à esquerda de Q) não
existe valor de f (ou de y) menor do que 6. Quando isso acontece, dizemos que a função y  f  x 
apresenta um mínimo local em Q.
Profa. Lena Bizelli
Em outras palavras, em x = 4, existe um mínimo local da função y  f  x  .
1) Quando escrevemos “extremos de uma função”, devemos especificar se estamos nos
referindo a extremos absolutos ou locais.
2) Os extremos locais de uma função y  f  x  só ocorrem no interior de um intervalo (ou
seja, não ocorrem nas extremidades de um intervalo).
3) Um extremo absoluto pode ser um extremo relativo, desde que este não ocorra nas
extremidades de um intervalo.
4) Quando escrevemos “ponto de máximo ou de mínimo da função y  f  x  ", estamos nos
referindo ao par ordenado  x, y  .
Quando escrevemos “valor máximo ou valor mínimo da função y  f  x  ", estamos nos
referindo ao valor da variável dependente y.
5) Outra maneira de se referir a um extremo de uma função y  f  x  é:
“em x = a existe um ponto de máximo ou de mínimo da função y  f  x  . ”
“em x = a existe um valor máximo ou mínimo da função y  f  x  . ”
Profa. Lena Bizelli