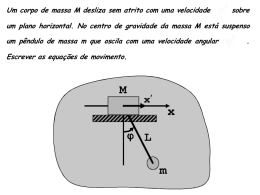
2/3/2014
Revisão de Física
Leis de Newton
1 – Equações de EulerLagrange
Dinâmica angular
Momento angular
TÓPICOS FUNDAMENTAIS DE
FÍSICA
© www.fisica-interessante.com 2/3/2014
Torque
1
© www.fisica-interessante.com 2/3/2014
Revisão de Física
Revisão de Física
Conservações
Trabalho
2
De momento linear
Energia cinética
De momento angular
© www.fisica-interessante.com 2/3/2014
3
© www.fisica-interessante.com 2/3/2014
Sistemas de partículas
Sistemas de partículas
Forças externas e internas
Referencial do centro de massa
4
Centro de massa
Decomposição das velocidades (D. Bernoulli,
1726)
© www.fisica-interessante.com 2/3/2014
5
© www.fisica-interessante.com 2/3/2014
6
1
2/3/2014
Sistemas de partículas
Vínculos
Momento angular
Holonômicos (‘lei inteira’)
Ex.: Corpo rígido:
Energia cinética
Não-holonômicos
Ex.: Gás num recipiente:
© www.fisica-interessante.com 2/3/2014
7
Vínculos
© www.fisica-interessante.com 2/3/2014
8
Sistemas de coordenadas
Problemas:
Esféricas,
1. Coordenadas não são mais independentes.
Hiperbólicas,
⇒ Eqs. de movimento não são mais independentes
Holonômicos ⇒ Introduzir coordenadas
generalizadas
Elípticas,
Cilíndricas,
etc.
2. Forças de vínculo são desconhecidas e
descobri-las é resolver o problema.
⇒ Formular mecânica de forma que desapareçam.
© www.fisica-interessante.com 2/3/2014
9
Coordenadas polares
© www.fisica-interessante.com 2/3/2014
10
Coordenadas polares
Posição, velocidade e aceleração
Derivadas:
Versores:
Força centrípeta e força de Coriolis
© www.fisica-interessante.com 2/3/2014
11
© www.fisica-interessante.com 2/3/2014
12
2
2/3/2014
Força de Coriolis
Coordenadas generalizadas
Generalizadas
© www.fisica-interessante.com 2/3/2014
13
Coordenadas generalizadas
© www.fisica-interessante.com 2/3/2014
Sistema de coordenadas curvilíneas sobre o
espaço (variedade) de configuração de um
mecanismo ou sistema mecânico com um
número finito N de graus de liberdade.
Podem ser
O estado físico de um sistema mecânico é
representado por um ponto do espaço de
configuração "ampliado" dimensão 2N.
© www.fisica-interessante.com 2/3/2014
14
Coordenadas generalizadas
N partículas: 3N coordenadas + k equações de
vínculo
⇒ 3N-k coordenadas generalizadas (graus de
liberdade)
Ex.:
15
as amplitudes de uma expansão de Fourier de r,
quantidades com dimensões de energia ou de
momento angular,
etc.
Pêndulo duplo: θ1, θ2
© www.fisica-interessante.com 2/3/2014
Princípio de D’Alambert
Princípio de D’Alambert
Num sistema em equilíbrio, o trabalho
Em termos das coordenadas generalizadas,
16
realizado por deslocamentos virtuais é nulo.
onde
⇒
© www.fisica-interessante.com 2/3/2014
17
© www.fisica-interessante.com 2/3/2014
18
3
2/3/2014
Equações de Euler-Lagrange
Equações de Euler-Lagrange
Para forças deriváveis de um potencial
escalar,
Criadas por Leonhard Euler e Joseph Louis
Lagrange na década de 1750.
⇒
onde
© www.fisica-interessante.com 2/3/2014
19
© www.fisica-interessante.com 2/3/2014
Ação
Mecânica Lagrangeana
Formulação da mecânica clássica que combina a
conservação do momento linear com a
conservação da energia.
A evolução de um sistema físico é descrita pela
solução da Equação de Euler-Lagrange para a
ação do sistema.
© www.fisica-interessante.com 2/3/2014
21
Equivalente às leis de Newton do movimento.
Vantagem: possui a mesma forma
independente do sistema de coordenadas
generalizadas utilizado.
Baseada num formalismo escalar mais simples
e geral do que o formalismo vetorial de
newtoniano.
Descreve igualmente bem fenômenos a baixas
velocidades ou a velocidades relativísticas.
© www.fisica-interessante.com 2/3/2014
Conceito criado por
Maupertuis e Euler.
Integral temporal, ao
longo do percurso do
ponto A ao ponto B,
da vis viva, isto é, do
dobro da energia
cinética.
© www.fisica-interessante.com 2/3/2014
22
Mecânica Lagrangeana
Mecânica Lagrangeana
20
Roteiro:
1. Expressar T e V em coordenadas generalizadas
2. Calcular L e suas derivadas
3. Aplicar na EqEL
23
4
2/3/2014
Exemplo
Exemplo
Partícula livre no espaço (coord. cartesianas)
Partícula livre no espaço (coord. polares)
e
e
e
© www.fisica-interessante.com 2/3/2014
25
Exemplo
Exemplo
Máquina de Atwood
Pérola deslizando por fio girando por eixo
perpendicular
⇒
⇒
Exemplo
Pêndulo sobre um suporte móvel
5