Intervalos
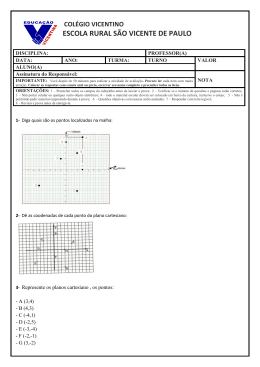
Reais
Intervalos Reais :
Parte da Reta ou
Subconjunto da Reta
a) Intervalo Aberto :
A = { x R / 2 < x < 6}
2
( 2 , 6 ) ou  2 , 6 
6
b) Intervalo Fechado :
A = { x R / 3  x  7}
[3,7]
3
7
1
5
c) Intervalo Semi-Aberto ou Semi-Fechado :
A = { x R / 1  x  5 }
] 1 , 5 ] ou ( 1 , 5 ]
1) Represente os subconjuntos abaixo na reta
e em forma de intervalos :
a) A = { x R / 3  x  4 }
b) A = { x  R / x  7 }
c) A = { x  R / x  5 }
d) A = { x  R / x  4 }
e) A = R
a) A = { x R / 3  x  4 }
3
4
b) A = { x  R / x  7 }
[3, 4)
(-  , 7 )
7
c) A = { x  R / x  5 }
[5, + )
5
d) A = { x  R / x  4 }
4
(- , 4 ) 
e) A = R
( 4,   )
( - , +  )
2) Sejam os conjuntos:
A = [ -2, 8 ) , B = ( 4 , 10 ) e C = [ 1, 13 ).
Determine :
a) ( A  B )  C
A
-2
8
4
B
10
A  B
10
-2
C
1
1
13
[ 1 , 10 )
10 ( A  B )  C
B) A - B
A
-2
8
B
4
-2
C) C A
4
10
A  B
[ -2, 4]
A
-2
8
CA
-2
8
(- , - 2 )  [ 8 , + )
3) Se
A  { x  R/ x  1} , B  {x  R/ - 1  x  3 }
e C  { x  R/ x  0 } . , então o conjunto que representa ( A  B ) - C é :
A  { x  R/ x  1 }
B  {x  R/ - 1  x  3 }
1
-1
3
AB
-1
1
-1
1
AB
C  { x  R/ x  0 }
0 a) {x  R/ - 1  x  0 }
(AB)-C
-1
0
EXERCÍCIO DO LIVRO: UFMG 1979 – 2004
PÁGINA 3 – EXERCÍCIO 04
O conjunto X é constituído dos elementos 0
e 2 e o conjunto y é o intervalo fechado
[ 1,2 ] = { y  R / 1  y  2 } . O conjunto X + Y,
definido por X + Y = { x + y ; x  X e y  Y } ,é :
a) [ 0,2 ]
b) [ 1,2 ]
c) [ 1,2 ]  { 0 }
d) [ 1,4 ]
e) [ 1,2 ]  [ 3,4 ]
X = { 0,2 }
y = [ 1,2 ]
1
Para x = 0 , teremos :
2
0 +
X + Y
1
Que será
1
Para x = 2 , teremos :
2
2
2 +
X + Y
1
Que será
3
2
4
X + Y = [ 1,2 ]  [ 3,4 ]
5) Sendo R o conjunto dos números reais,
A x  R/ -5 x  4  e Bx  R/ -3 x  7 
O conjunto A – B é igual a :
a)  x  R / 4  x  7 
 x R /
 x R /
d)  x  R /
e)  x R /
b)
c)
-5 x -3 
-3 x  4 
-5 x -3 
4x7
A  { x  R/ - 5  x  4 }
-5
4
B  {x  R/ - 3  x  7 }
-3
AB
-5
-3
A - B   x R / - 5  x  - 3 
7
PLANO
CARTESIANO
Eixo ¨ Y ¨
( Eixo das ordenadas )
{
P( x , y )
Coordenadas do ponto
II Quadrante
I Quadrante
Eixo ¨ X ¨
( Eixo das abscissas )
III Quadrante
IV Quadrante
Exercício :
Marque V ( verdadeiro) ou F ( falso ) :
a) O ponto
A ( - 1+ 2 , 7 ) está no 2° quadrante.
b) O ponto B ( a , 0 ) está sobre o eixo x .
c) O ponto C (  - 4 ,-1- 3 )
3° quadrante.
está no
d) O ponto D ( 0 , a ) está sobre o eixo y .
e) O ponto E ( a , - b ) , onde a > 0 e b < o
está no 4° quadrante.

A - 1
2 ,7
(V)

C  - 4 , - 1-
(V)

D
 0,a 
(V)
E ( 2 , 1 )( Falsa )
B a,0  ( V )
3

a > 0 ... a = 2
b < o ... b = -1
E(2,1)
Produto Cartesiano:
Dados dois conjuntos A e B , chama-se de produto
cartesiano de A por B :
AxB= {(x, y); x  Ae y  B}
Exemplo :
A={1,2} e B={1,3,4}
a) A x B = { (1,1) , ( 1, 3) , ( 1,4) , ( 2,1) , ( 2,3) , ( 2,4) }
b) B x A = { (1,1) , ( 1, 2) , ( 3,1) , ( 3,2) , ( 4,1) , ( 4,2) }
c) A 2 = A x A = { ( 1,1) , ( 1, 2) , ( 2,1) , ( 2,2) }