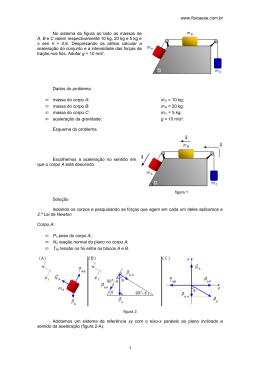
www.fisicaexe.com.br
Uma máquina de Atwood é disposta de
tal maneira que as massas móveis M1 e M2 ao
invés de se moverem verticalmente, são
obrigadas a deslizar sem atrito sobre dois
planos inclinados de 30º e 60º em relação a
horizontal. Supõe-se que os fios que sustentam
as massas M1 e M2 são paralelos as retas de
maior declive desses planos. Determinar:
a) A relação entre M1 e M2 para que o sistema
permaneça em equilíbrio;
b) Calcular a aceleração do movimento e a tensão no fio quando as massas são iguais, cada
uma, a 5 kg.
2
Dada a aceleração da gravidade igual a 9,81 m/s .
Dados do problema
•
•
M 1 = M 2 = 5 kg;
2
g = 9,81 m/s .
massa dos blocos:
aceleração da gravidade:
Esquema do problema
Adota-se um sentido aleatório para a aceleração, figura 1
figura 1
Isolando os corpos e pesquisando as forças que agem neles, temos
Corpo de massa M 1
Adotamos um sistema de referência xy com o eixo-x paralelo ao plano inclinado e
r
r
sentido da aceleração. Neste corpo agem a força peso ( P1 ), a força de tensão no fio ( T ) e a
r
reação normal da superfície ( N 1 ), conforme a figura 2-A.
•
figura 2
1
www.fisicaexe.com.br
r
A força peso pode ser decomposta em duas, uma componente paralela ( P1P ) ao eixo-x
r
e a outra normal ou perpendicular ( P1N ). Da figura 2-B vemos que a força peso é perpendicular
ao plano horizontal, forma um ângulo de 90º, o ângulo entre o plano inclinado, que contém a
componente paralela, e o plano horizontal é dado como 60º, como os ângulos internos de um
triângulo devem somar 180º o ângulo entre a força peso e a componente paralela deve ser 30º.
No triângulo à direita temos que a componente normal faz com o plano inclinado um ângulo de
90º então o ângulo entre a força peso e a componente normal deve medir 60º, é um ângulo
complementar.
Colocando as forças num sistema de eixos coordenados, figura 2-C, podemos usar a
2.ª Lei de Newton
r
r
F = m .a
Na direção y não há movimento, a reação normal e a componente normal do peso se
anulam, na direção x escrevemos em módulo
T − P1P sen 60° = M 1 a
T − M 1 g sen 60° = M 1 a
(I)
•
Corpo de massa M 2
Da mesma forma adotamos um sistema de referência xy com o eixo-x paralelo ao
r
plano inclinado e sentido da aceleração. Neste corpo agem a força peso ( P 2 ), a força de
r
r
tensão no fio (T ) e a reação normal da superfície ( N 2 ), conforme a figura 3-A.
figura 3
Analogamente a força peso pode ser decomposta em duas, uma componente paralela
r
r
( P2P ) ao eixo-x e a outra normal ou perpendicular ( P 2N ), figura 3-B, neste caso o ângulo entre
a força peso e a componente normal será 30º.
E colocando as forças num sistema de eixos coordenados, figura 3-C, podemos usar a
2.ª Lei de Newton. Na direção y não há movimento, a reação normal e a componente normal do
peso se anulam, na direção x escrevemos em módulo
P2P sen 30° − T = M 2 a
M 2 g sen 30° − T = M 2 a
(II)
Solução
a) Para que o sistema permaneça em equilíbrio devemos ter a aceleração igual a zero (a = 0),
substituindo este valor e os valores do seno e co-seno nas equações (I) e (II) temos o seguinte
sistema de equações
2
www.fisicaexe.com.br
T − M1 g
M2 g
3
2
=0
1
−T = 0
2
3
=T
2
1
M2 g =T
2
M1 g
(III)
(IV)
dividindo a equação (IV) por (III)
1
2 =T
3 T
M 1.g .
2
1
M2.
2 =1
3
M1.
2
M2
3 2
.
=
2 1
M1
M 2 .g .
M2
M1
=
3
b) Para encontrarmos a aceleração e a tensão usamos as equações (I) e (II) e fazemos
M 1 = M 2 = M = 5 kg
3
T −M g
Mg
2
=M a
1
−T = M a
2
(V)
(VI)
Este é um sistema de duas equações a duas incógnitas, a aceleração a e a tensão T,
somando estas duas equações temos
T − M .g .
(+ )
3
= M .a
2
1
− T = M .a
2
3
1
− M .g .
+ M . g . = M .a + M .a
2
2
M .g .
3
1
+ M .g . = 2 M .a
2
2
3
1 
1
+ M .g . 
. − M . g .
a=
2 M 
2
2 
− M .g .
substituindo os valores dados para a massa e para a aceleração da gravidade
3
www.fisicaexe.com.br
a=
3
1
1 
. − 5 . 9,81.
+ 5 . 9,81. 
2 
2
2 . 5 
a=
1
. [− 42,48 + 24,53]
10
a = −1,79 m/s 2
o sinal de negativo na aceleração indica que o sentido do movimento será contrário àquele
adotado na figura 1.
Subtraindo as equações (V) e (VI), obtemos
T − M .g .
(− )
3
= M .a
2
1
− T = M .a
2
3
1
− M .g .
− M . g . + 2T = 0
2
2
M .g .
2T = M . g .
T =
3
1
+ M .g .
2
2
3
1
1 
+ M .g . 
.  M .g .
2 
2
2 
substituindo os valores do problema
T =
3
1 
1
.  5 . 9,81.
+ 5 . 9,81. 
2 
2
2 
T =
1
. [ 42,48 + 24,53 ]
2
T = 33,51 N
4