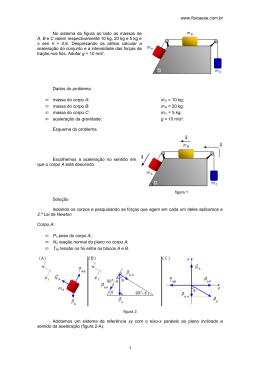
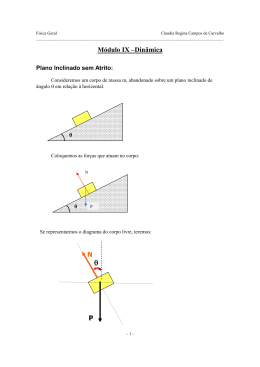
www.fisicaexe.com.br
Um corpo de massa 200 kg é mantido em
equilíbrio sobre um plano inclinado de 30º em relação
à horizontal mediante um fio que passa por uma polia
fixa e que sustenta na outra extremidade um corpo de
massa M. O fio forma com a reta de maior declive do
plano um ângulo de 45º. Determinar:
a) A massa M;
b) A força exercida pelo corpo contra o plano.
Dados do problema
•
•
•
massa do corpo no plano inclinado:
ângulo do plano inclinado com a horizontal:
ângulo da corda com o plano inclinado:
m = 200 kg;
30º;
45º.
Esquema do problema
Em primeiro lugar vamos isolar os corpos e pesquisar as forças que agem sobre cada
um e como o sistema está em equilíbrio devemos ter que a somatória de todas as forças seja
igual a zero
∑F = 0
(I)
Corpo de massa M
•
•
T: tensão na corda;
P M peso do corpo suspenso.
Como só existem forças atuando no corpo na direção vertical (figura 1) pela
condição de equilíbrio (I) temos, em módulo
T −P M = 0
(II)
figura 1
Corpo de massa 200 kg
•
•
•
T: tensão na corda, tem o mesmo valor em módulo que a
tensão que age sobre o bloco anterior;
P I: peso do corpo no plano inclinado;
N: reação normal do plano sobre o bloco.
Vamos analisar as forças em duas direções, na direção
paralela ao plano inclinado (chamada de x) e na direção
figura 2
perpendicular a este (chamada de y).
Devemos achar o ângulo que a força peso forma com as direções perpendicular (y) e
paralela (x) ao plano inclinado (figura 3).
1
www.fisicaexe.com.br

O ângulo Q AM
é dado no problema como
sendo 30º, o segmento 
Q M (direção onde está a
força peso) é perpendicular ao segmento AC , como
a soma dos ângulos internos de um triângulo deve
 M deve ser
valer 180º então o ângulo A Q
 M 30o 90o = 180o
AQ
 M = 180 o−30o −90o
AQ
A Q M = 60o
figura 3
Para determinarmos o valor do ângulo , figura 4, vamos ampliar
 M vale
a região em vermelho da figura 3. Já sabemos que o ângulo A Q


60º e o segmento Q N é perpendicular ao segmento AB (forma um
ângulo de 90º). então a soma destes ângulos com o ângulo  procurado
deve ser 180º, assim
o
o
o
60 90  = 180
 = 180o −60o −90o
o
 = 30
Desenhando as forças num sistema de eixos coordenados como
mostra a figura 5 podemos obter suas componentes, em módulo, ao longo
das direções x e y.
figura 4
componentes ao longo do eixo x
•
•
•
Nx = 0
o
T x = T cos 45
o
P i x = −P i cos 60
Aplicando a condição de equilíbrio dada em (I) a estas
equações temos
o
o
N x T cos 45 −P i cos 60 = 0
o
o
T cos 45 −P i cos60 = 0
(III)
componentes ao longo do eixo y
•
•
•
figura 5
Ny = N
o
T y = T sen 45
o
P i y = −P i sen 60
Da condição (I) escrevemos
o
o
NT sen 45 −P i sen 60 = 0
(IV)
Solução
a) Sendo a força peso dada por
P = mg
2 ,
1
o
 3 as
e sen 60 =
2
2
2
equações (II), (III) e (IV) formam um sistema de três equações a três incógnitas (N, T e M)
o
o
e lembrando da Trigonometria que cos 45 =´ sen 45 =
2
o
cos60 =´
www.fisicaexe.com.br
∣
T −M g = 0
 2 T −1 m g = 0
2
2
2
3
N  T −  m g = 0
2
2
(V)
(VI)
(VII)
isolando o valor da tensão na equação (V), temos
T =Mg
(VIII)
e substituindo em (VI)
 2 M g− 1 m g = 0
2
2
2
 M g = 1 mg
2
2
simplificando o valor de g e o 2 no denominador
2 M = m
M=
m
2
substituindo o valor de m dado no problema e sendo
M=
 2 ≈ 1,4142 , obtemos
200
1,4142
M = 141,4 kg
b) A força exercida sobre o plano ( F p ) será dada pela componente y do bloco sobre o plano
inclinado
F p = P i y = −P i sen 60
o
adotando-se o valor de 10 m/s2 para a aceleração da gravidade na Terra (já que o problema
não dá este valor), temos
F p =−200 .10 .
sendo
3
2
 3 ≈ 1,7321 , temos
F p = −1732 N
3