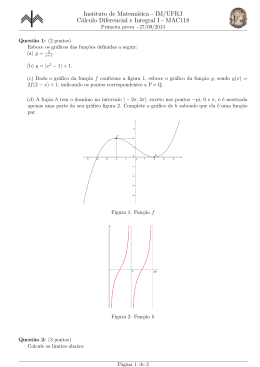
Matemática II (CG) / Análise Matemática (IG)
DERIVAÇÃO de FUNÇÕES REAIS de VARIÁVEL REAL
Derivada de uma função num ponto.
Sejam f uma função denida num intervalo A ⊆ R e a um ponto de acumulação de
A. Chama-se derivada de f no ponto a ao limite, caso exista:
lim
x→a
f (x) − f (a)
x−a
A derivada de f no ponto a designa-se por f 0 (a), Df ou
x=a
df
dx x=a
.
Designando por h o acréscimo x − a, a denição de derivada de f no ponto a pode
ser escrita na seguinte forma:
f (a + h) − f (a)
h→0
h
f 0 (a) = lim
Derivadas laterais.
Pode não existir derivada num ponto x = a, mas existirem derivadas laterais. Nesse
caso, denem-se as derivadas laterais de f no ponto a do seguinte modo:
ˆ f 0 (a− ) = lim−
f (x)−f (a)
x−a
(derivada à esquerda de f no ponto a),
ˆ f 0 (a+ ) = lim+
f (x)−f (a)
x−a
(derivada à direita de f no ponto a).
x→a
x→a
Uma condição necessária e suciente para que a função f tenha derivada no ponto
a é que:
f 0 (a− ) = f 0 (a+ )
A derivada de uma função num ponto pode ser nita ou innita. Se a derivada de
f num ponto a é nita, f diz-se derivável nesse ponto.
Interpretação geométrica.
A derivada de uma função f no ponto a é igual ao declive da recta tangente ao
gráco de f no ponto (a, f (a)).
Aulas teóricas: resumo 2
página: 1/15
Matemática II (CG) / Análise Matemática (IG)
Função derivada.
Se a função f admite derivada nita em todos os pontos de um intervalo A, a cada
ponto a ∈ A corresponde um e um só número real f 0 (a), cando assim denida em
A uma nova função f 0 (x) que se diz função derivada da função f em ordem a x.
Essa função pode representar-se por:
f0
Df
ou
df
dx
Derivadas de ordem superior à primeira.
Seja f uma função com derivada em todos os pontos de um intervalo A.
Se a função f 0 tiver derivada nita em todos os pontos desse intervalo, ca denida
uma nova função que se diz função derivada de segunda ordem de f e que se designa
por:
f 00
D2 f
ou
d2 f
dx2
Continuidade e derivabilidade.
Toda a função que admite derivada nita num ponto é contínua nesse ponto.
A única forma de existir e ser nito o limite:
lim
x→a
f (x) − f (a)
x−a
é ter
lim f (x) = f (a)
x→a
Nota: o recíproco deste teorema não é verdadeiro: uma função pode ser contínua
num dado ponto e não ser derivável nesse ponto. Um exemplo simples é o da função
g(x) = |x|, que é contínua em x = 0 mas não é derivável nesse ponto.
Aulas teóricas: resumo 2
página: 2/15
Matemática II (CG) / Análise Matemática (IG)
Cálculo de derivadas pela denição:
(k)0 =
(k · x)0 =
k · x2
0
=
=
lim
k−k
= lim 0 = 0
h→0
h
lim
k · (x + h) − k · x
k·h
= lim
= lim k = k
h→0 h
h→0
h
lim
2khx + kh2
k · (x + h)2 − k · x2
= lim
=
h→0
h
h
h→0
h→0
h→0
lim 2kx = 2kx
h→0
g(x + h) + s(x + h) − g(x) − s(x)
=
h→0
h
g(x + h) − g(x) s(x + h) − s(x)
= lim
+
= g 0 (x) + s0 (x)
h→0
h
h
[g(x) + s(x)]0 =
[g(x) · s(x)]0 =
=
lim
lim
g(x + h) · s(x + h) − g(x) · s(x)
=
h
lim
g(x + h)s(x + h) − g(x)s(x) − g(x + h)s(x) + g(x + h)s(x)
=
h
h→0
h→0
s(x) [g(x + h) − g(x)] + g(x + h) [s(x + h) − s(x)]
=
h→0
h
s(x + h) − s(x)
g(x + h) − g(x)
= lim s(x)
+ g(x + h)
=
h→0
h
h
=
lim
= g 0 (x) · s(x) + g(x) · s0 (x)
Aulas teóricas: resumo 2
página: 3/15
Matemática II (CG) / Análise Matemática (IG)
g(x)
s(x)
0
=
=
=
=
=
0
(sen x)
0
(cos x)
lim
g(x+h)
s(x+h)
−
h
h→0
g(x)
s(x)
=
lim
g(x + h)s(x) − g(x)s(x + h)
=
h s(x + h) s(x)
lim
g(x + h)s(x) − g(x)s(x + h) − g(x)s(x) + g(x)s(x)
=
h s(x + h) s(x)
lim
s(x) g(x+h)−g(x)
− g(x) s(x+h)−s(x)
h
h
=
s(x + h) s(x)
h→0
h→0
h→0
g 0 (x) · s(x) − g(x) · s0 (x)
[s(x)]2
2sen
sen (x + h) − sen (x)
= lim
= lim
h→0
h→0
h
!
sen h2
2x + h
= lim
cos
= cos x
h
h→0
2
2
h
2
cos
h
−2sen h2 sen
cos (x + h) − cos (x)
= lim
= lim
h→0
h→0
h
h
!
sen h2
2x + h
= lim −
sen
= −sen x
h
h→0
2
2
2x+h
2
=
2x+h
2
=
onde se utilizaram as relações:
α−β
α+β
cos
2
2
α+β
α−β
cos α − cos β = −2sen
sen
2
2
sen α − sen β = 2sen
lim
x→0
Aulas teóricas: resumo 2
sen x
=1
x
página: 4/15
Matemática II (CG) / Análise Matemática (IG)
Regras de derivação.
u = f (x)
k = constante
v = g(x)
a = constante
• (u ± v)0 = u0 ± v 0
• (u · v)0 = u0 · v + u · v 0
•
u 0
v
u0 · v − u · v 0
=
v2
(v 6= 0)
• (k)0 = 0
• (k · u)0 = k · u0
•
xk
0
= k xk−1
a ∈ R+
(ax )0 = ax · ln a
(loga x)0 =
1
x ln a
x ∈ R+ , a ∈ R+ \ {1}
(sen x)0 = cos x
(cos x)0 = −sen x
(arcsen x)0 = √
(arctg x)0 =
Aulas teóricas: resumo 2
1
1 − x2
−1<x<1
1
1 + x2
página: 5/15
Matemática II (CG) / Análise Matemática (IG)
Derivada da função composta.
Se f (x) é uma aplicação de A em R:
A⊂R
f : x → u = f (x)
derivável num ponto a do seu domínio, e g(x) é uma aplicação de B em R, tal que
f (A) ⊂ B :
B⊂R
g : u → y = g(u)
derivável no ponto b = f (a), então a função:
g◦f : A→R
é derivável em a e:
(g ◦ f )0 (a) = g 0 (b) · f 0 (a)
De um modo geral, em pontos correspondentes tem-se:
(g ◦ f )0 (x) = g 0 (u) · f 0 (x)
ou, utilizando outra notação:
dy
dy du
=
·
dx
du dx
Derivada da função inversa.
A⊂R
f : x → u = f (x)
Se a função f denida acima é uma aplicação de A em R, invertível, com derivada
não nula num ponto a do seu domínio, então f −1 : f (A) → A é derivável no ponto
b = f (a) e:
f −1
0
=
1
f 0 (a)
ou, utilizando outra notação:
dx
1
= du
du
dx
Aulas teóricas: resumo 2
página: 6/15
Matemática II (CG) / Análise Matemática (IG)
ALGUNS TEOREMAS
Teorema de Rolle.
Se f : [a, b] → R, com a < b, é uma função contínua em [a, b], derivável em todos
os pontos de ]a, b] e se f (a) = f (b), então existe pelo menos um ponto c ∈ ]a, b[, tal
que f 0 (c) = 0.


f contínua em [a, b] 





f derivável em ]a, b[







f (a) = f (b)
⇒ ∃ c ∈ ]a, b[ : f 0 (c) = 0
Interpretação geométrica.
Geometricamente, o teorema de Rolle arma que o gráco da função f admite, pelo
menos, uma tangente horizontal num ponto interior a ]a, b[.
Demonstração
Sendo f (x) contínua no intervalo fechado [a, b], o teorema de Weierstrass
garante que o conjunto f ([a, b]) é limitado, isto é, tem um máximo (M) e
um mínimo. Existem, assim, quatro possibilidades:
ˆ A função f atinge o seu valor máximo e mínimo no interior do intervalo
aberto ]a, b[. Como f é derivável em ]a, b[, nos dois pontos correspondentes f 0 = 0.
ˆ A função f atinge o seu valor máximo nos extremos e o seu valor mínimo
no interior do intervalo aberto ]a, b[. Como f é derivável em ]a, b[, no
ponto onde f é mínimo temos f 0 = 0.
ˆ A função f atinge o seu valor mínimo nos extremos e o seu valor máximo
no interior do intervalo aberto ]a, b[. Como f é derivável em ]a, b[, no
ponto onde f é máximo temos f 0 = 0.
ˆ A função f atinge o seu valor máximo e o seu valor mínimo nos extremos.
Como f (a) = f (b), neste caso f é constante em [a, b] e portanto f 0 (x) =
0 , ∀x ∈]a, b[.
Aulas teóricas: resumo 2
página: 7/15
Matemática II (CG) / Análise Matemática (IG)
Corolários do teorema de Rolle.
1. Seja f : [a, b] → R, com a < b, uma função contínua em [a, b], derivável em
todos os pontos de ]a, b] . Se a e b são dois zeros distintos de f, então a função
f' admite pelo menos um zero em ]a, b[.
f contínua em [a, b]
f derivável em ]a, b[
f (a) = f (b) = 0



⇒ ∃ c ∈ ]a, b[ : f 0 (c) = 0


2. Seja I ⊂ R , f : I → R derivável em I e seja [a, b] ⊂ I . Se a e b são zeros
consecutivos da função derivada f 0 , então não pode haver mais do que um zero
de f no intervalo ]a, b[.
f derivável em I
[a, b] ⊂ I
f 0 (a) = f 0 (b) = 0
f 0 (x) 6= 0 , ∀ x ∈ ]a, b[









⇒
entre a e b não pode haver
mais do que um zero de f .
Nota: Atendendo ao teorema de Bolzano sobre funções contínuas, podemos
armar que:
ˆ Se f (a) e f (b) tiverem sinais contrários, existe um zero de f em ]a, b[.
ˆ Se f (a) e f (b) tiverem o mesmo sinal, não há nenhum zero de f em ]a, b[.
3. Seja I ⊂ R , f : I → R derivável em I . Se c é o menor (maior) zero da função
derivada f 0 , não pode haver mais do que um zero de f menor (maior) que c.
Aulas teóricas: resumo 2
página: 8/15
Matemática II (CG) / Análise Matemática (IG)
Teorema de Lagrange ou do valor médio.
Se f : [a, b] → R, com a < b, é uma função contínua em [a, b], derivável em ]a, b[,
então existe pelo menos um ponto c ∈ ]a, b[, tal que:
f 0 (c) =
f contínua em [a, b]
f derivável em ]a, b[
f (b) − f (a)
b−a
)
⇒ ∃c ∈ ]a, b[ : f 0 (c) =
f (b) − f (a)
b−a
Interpretação geométrica do teorema de Lagrange.
Geometricamente, o teorema de Lagrange garante que, entre os pontos do gráco
de abcissas a e b, há pelo menos um ponto desse gráco onde a tangente é paralela
à secante denida pelos pontos (a, f (a)) e (b, f (b)).
Demonstração
Considere-se a função:
h(x) = f (x) −
f (b) − f (a)
(x − a)
b−a
Verica-se facilmente que:
ˆ Se f é contínua em [a, b], h também é.
ˆ Se f é derivável em ]a, b[, h também é.
ˆ h(a) = h(b) = f (a)
Assim, o teorema de Rolle garante que existe pelo menos um c ∈]a, b[ tal que
h0 (c) = 0.
h0 (c) = 0 ⇔ f 0 (c) −
Aulas teóricas: resumo 2
f (b) − f (a)
f (b) − f (a)
= 0 ⇔ f 0 (c) =
b−a
b−a
página: 9/15
Matemática II (CG) / Análise Matemática (IG)
Aplicação das derivadas ao estudo do comportamento de funções
Denições:
ˆ Uma função diz-se estritamente
crescente num intervalo I se
∀x1 , x2 ∈ I , x1 < x2 ⇒ f (x1 ) < f (x2 )
ˆ Uma função diz-se estritamente
decrescente num intervalo I se
∀x1 , x2 ∈ I , x1 < x2 ⇒ f (x1 ) > f (x2 )
NOTA: Se
∀x1 , x2 ∈ I , x1 < x2 ⇒ f (x1 ) ≤ f (x2 ), a função diz-se crescente em sentido lato.
Da mesma forma, se
∀x1 , x2 ∈ I , x1 < x2 ⇒ f (x1 ) ≥ f (x2 ),
a função diz-se decrescente
em sentido lato.
Corolários do teorema de Lagrange.
Seja f : [a, b] → R uma função contínua em [a, b] e derivável em ]a, b[. Então:
1. f 0 (x) > 0 ∀x ∈ ]a, b[
⇒ f (x) é estritamente crescente em [a, b].
2. f 0 (x) < 0 ∀x ∈ ]a, b[
⇒ f (x) é estritamente decrescente em [a, b].
3. f 0 (x) = 0 ∀x ∈ ]a, b[
⇒ f (x) é constante em [a, b].
Se a função f for duplamente derivável
1. f 00 (x) > 0 ∀x ∈ ]a, b[
⇒ f 0 (x) é estritamente crescente em [a, b], logo a
função f tem a concavidade voltada para cima (∪) nesse intervalo.
2. f 00 (x) < 0 ∀x ∈ ]a, b[
⇒ f 0 (x) é estritamente decrescente em [a, b], logo
a função f tem a concavidade voltada para baixo (∩) nesse intervalo.
Teorema: Se f possui um máximo ou um mínimo para x = c, então f 0 (c) = 0 ou
f 0 (c) não existe.
Os pontos onde f 0 = 0 ou f 0 não existe designam-se pontos críticos de f .
Os pontos onde f 00 = 0 ou f 00 não existe designam-se pontos de inexão de f .
Aulas teóricas: resumo 2
página: 10/15
Matemática II (CG) / Análise Matemática (IG)
Uma aplicação de derivadas:
Problemas de Optimização
Em problemas da vida real (ou de outras ciências que não a matemática), procuramse frequentemente as soluções "óptimas". Muitas vezes, esta solução "óptima"é
encontrada determinando os extremos (máximos e mínimos) de uma dada função.
A qualquer problema onde esteja em causa encontrar a solução "óptima"chama-se
problema de optimização.
Para resolver um problema de optimização, adopta-se o seguinte procedimento:
1. Compreender o problema
Qual é a incógnita? Quais são os valores conhecidos? Quais são as condições
a que obedecem as variáveis?
2. Fazer um esquema
Quais são os dados para colocar no esquema?
3. Introduzir símbolos
Como representar as variáveis? Quais as letras mais apropriadas?
4. Exprimir a incógnita em função de uma só variável
Qual é a variável independente?
5. Usar métodos analíticos para encontrar a solução
Quais são os zeros da primeira derivada?
Quais são os extremos?
Aulas teóricas: resumo 2
página: 11/15
Matemática II (CG) / Análise Matemática (IG)
Teorema de Cauchy.
Sejam f : [a, b] → R e g : [a, b] → R com a < b, duas funções contínuas em [a, b] e
deriváveis em ]a, b[. Se g 0 (x) 6= 0 ∀ x ∈ ]a, b[, existe pelo menos um c pertencente a
]a, b[, tal que:
f (b) − f (a)
f 0 (c)
= 0
g(b) − g(a)
g (c)
f, g contínuas em [a, b]
f, g deriváveis em ]a, b[
g 0 (x) 6= 0 ∀ x ∈ ]a, b[



⇒ ∃ c ∈ ]a, b[ :


f 0 (c)
f (b) − f (a)
= 0
g(b) − g(a)
g (c)
Demonstração
Considere-se a função:
h(x) = [g(b) − g(a)] · f (x) − [f (b) − f (a)] · g(x)
Verica-se facilmente que:
ˆ Se f e g são contínuas em [a, b], h também é.
ˆ Se f e g são deriváveis em ]a, b[, h também é.
ˆ h(a) = h(b) = f (a) · g(b)
Assim, o teorema de Rolle garante que existe pelo menos um c ∈]a, b[ tal que
h0 (c) = 0.
h0 (c) = 0
⇔ [g(b) − g(a)] · f 0 (c) − [f (b) − f (a)] · g 0 (c) = 0
⇔ [g(b) − g(a)] · f 0 (c) = [f (b) − f (a)] · g 0 (c)
O teorema de Cauchy conduz-nos à Regra de Cauchy, que permite levantar facilmente diversos tipos de indeterminações.
Aulas teóricas: resumo 2
página: 12/15
Matemática II (CG) / Análise Matemática (IG)
Regra de Cauchy.
Sejam f e g duas funções deriváveis num intervalo aberto I , tal que g 0 (x) 6= 0 ∀ x ∈ I ,
e seja a um dos extremos de I . Se quando x tende para a (x → a), f (x)e g(x) tendem
0 (x)
(x)
para 0, ou para ±∞, e se existe lim fg0 (x)
, então existe também lim fg(x)
e tem-se:
x→a
x→a
f (x)
f 0 (x)
= lim 0
x→a g(x)
x→a g (x)
lim
Obs. A regra de Cauchy é ainda aplicável quando x → ±∞. Esta regra permite
∞
levantar indeterminações do tipo 00 e ∞
.
EXEMPLOS:
lim
x→0
lim
x→+∞
sen x
cos x
= lim
=1
x→0
x
1
ex
ex
ex
=
lim
=
lim
= +∞
x2 x→+∞ 2x x→+∞ 2
NOTA: A regra de Cauchy não permite levantar todas as indeterminações. Pode
acontecer que exista lim
f (x)
x→a g(x)
f 0 (x)
0
x→a g (x)
mas não exista lim
x + sen(x)
= lim
lim
x→+∞
x→+∞
x
. Por exemplo,
sen(x)
1+
x
=2
mas
1 + cos(x)
= lim (1 + cos(x))
x→+∞
x→+∞
1
(o cosseno oscila entre −1 e 1).
lim
Por outras palavras, a existência de lim
x→a
o contrário não é verdadeiro.
Aulas teóricas: resumo 2
f 0 (x)
g 0 (x)
não existe!
implica a existência de x→a
lim
f (x)
g(x)
, mas
página: 13/15
Matemática II (CG) / Análise Matemática (IG)
Representação gráca de funções reais de variável real
Determinação de assimptotas
ˆ
Assimptotas verticais:
Diz-se que a recta de equação x = a é uma assimptota vertical do gráco
da função f se:
ou
lim f (x) = ±∞
x→a+
ˆ
lim f (x) = ±∞
x→a−
Assimptotas horizontais:
Diz-se que a recta de equação y = b é uma assimptota horizontal do gráco
da função f se:
ou
lim f (x) = b
x→+∞
ˆ
lim f (x) = b
x→−∞
Assimptotas oblíquas:
Uma recta y = m · x + b ,
da função f se:
(m 6= 0) é uma
assimptota oblíqua do gráco
lim (f (x) − m · x − b) = 0
x→±∞
(o que signica que, quando x tende para ±∞, o gráco da função tende a
confundir-se com a recta de equação y = m · x + b
Na prática, determina-se:
m = lim
x→±∞
f (x)
x
b = lim (f (x) − m · x)
x→±∞
NOTA: Se m = 0 trata-se de uma assimptota horizontal, descrita no ponto
anterior.
Aulas teóricas: resumo 2
página: 14/15
Matemática II (CG) / Análise Matemática (IG)
Antes de esboçar o gráco de uma função, é conveniente determinar previamente:
ˆ O domínio da função.
ˆ Os pontos de intersecção com os eixos (zeros e ordenada na origem).
ˆ Os pontos de descontinuidade.
ˆ As simetrias do gráco (em relação à origem e ao eixo dos xx).
ˆ As assimptotas.
ˆ Os intervalos onde a função é crescente ou decrescente e os máximos e mínimos
relativos (estudo da primeira derivada).
ˆ A concavidade e os pontos de inexão (estudo da segunda derivada).
Para desenhar o gráco de uma função é por vezes necessário calcular as coordenadas
de mais alguns pontos.
Aulas teóricas: resumo 2
página: 15/15