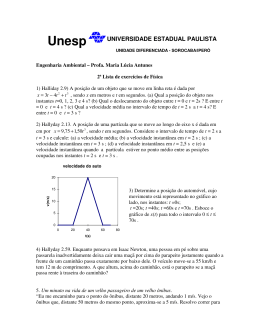
Problemas Resolvidos de Física
Prof. Anderson Coser Gaudio – Depto. Física – UFES
HALLIDAY, RESNICK, WALKER, FUNDAMENTOS DE FÍSICA, 8.ED., LTC, RIO DE
JANEIRO, 2008.
FÍSICA 1
CAPÍTULO 2 – MOVIMENTO RETILÍNEO
17. A posição de uma partícula que se move ao longo do eixo x é dada em centímetros por x = 9,75
+ 1,50 t3, onde t está em segundos. Calcule (a) a velocidade média durante o intervalo de tempo
de t = 2,00 s a t = 3,00 s; (b) a velocidade instantânea em t = 2,00 s; (c) a velocidade instantânea
em t = 3,00 s; (d) a velocidade instantânea em t = 2,50 s; (e) a velocidade instantânea quando a
partícula está na metade da distância entre suas posições em t = 2,00 s e t = 3,00 s. (f) Plote o
gráfico de x em função de t e indique suas respostas graficamente.
(Pág. 34)
Solução.
(a) Chamando de x 0 a posição da partícula em t 0 = 2,00 s e de x 1 sua posição em t 1 = 3,00 s, os
valores de x 0 e x 1 serão:
x0 =
9, 75 + 1,50 ( 2, 00 ) =
21, 75 cm
3
x1 =
9, 75 + 1,50 ( 3, 00 ) =
50, 25 cm
3
A velocidade média da partícula no intervalo de tempo t 1 − t 0 será:
vm=
,01
∆x x1 − x0
=
=
∆t t1 − t0
( 50, 25 cm ) − ( 21, 75 cm )
( 3, 00 s ) − ( 2, 00 s )
vm ,01 = 28,5 cm/s
(b) A velocidade instantânea v corresponde à derivada da função x(t) em relação a t:
dx d
v == 9, 75 + 1,50t 3 =
4,50t 2
dt dt
Logo, para t 0 = 2,00 s teremos:
(
)
v0 = 4,50 ( 2, 00 )
2
v0 = 18, 0 cm/s
(c) Para t 1 = 3,00 s teremos:
v1 = 4,50 ( 3, 00 )
2
v1 = 40,5 cm/s
(d) Para t 2 = 2,50 s teremos:
=
v2 4,50
=
( 2,50 ) 28,125 cm/s
2
v2 ≈ 28,1 cm/s
(e) A metade da distância entre as posições da partícula em t 0 = 2,00 s e t 1 = 3,00 s corresponde à
posição x 3 , definida por:
x3
=
x0 + x1
=
2
cm )
( 21, 75 cm ) + ( 50, 25=
2
36 cm
________________________________________________________________________________________________________
Halliday, Resnick, Walker - Fund.de Física 1 - 8a Ed. - LTC - 2009.
Cap. 02 – Movimento Retilíneo
1
Problemas Resolvidos de Física
Prof. Anderson Coser Gaudio – Depto. Física – UFES
A partícula alcança a posição x 3 no instante de tempo t 3 , que vale:
=
x3 9, 75 + 1,50t33
=
t3
( 36 − 9, 75)
= 2,5962 s
1,50
3
Logo, a velocidade v 3 da partícula no instante t 3 será:
=
v3 4,50
=
( 2,5962) 30,3322 cm/s
2
v3 ≈ 30,3 cm/s
(f)
x (cm)
Declividade = v1
Declividade = v3
x1
Declividade = v0
x3
x0
Declividade = vm01
1
2
t0
3
t1
t (s)
t3
________________________________________________________________________________________________________
Halliday, Resnick, Walker - Fund.de Física 1 - 8a Ed. - LTC - 2009.
Cap. 02 – Movimento Retilíneo
2