Escola Básica e Secundária Dr. Ângelo Augusto da Silva
Teste de MATEMÁTICA A 11º Ano
Duração: 90 minutos
Classificação
Março/ 2010
____________
Nome ________________________ Nº ___ T: __
O Prof.__________________
(Luís Abreu)
1ª PARTE
Para cada uma das seguintes questões de escolha múltipla, seleccione a resposta correcta de entre as alternativas
que lhe são apresentadas e escreva-a na sua folha de prova. Se apresentar mais do que uma resposta a questão será
anulada, o mesmo acontecendo em caso de resposta ambígua.
1. Considere a função g, definida em \ , por
⎧⎪ 4 x 2 + 9 se x ≥ 0
g ( x) = ⎨ 2
⎪⎩ x − 9 se x < 0 .
Qual é o conjunto dos zeros de g?
(A) {−3, 3}
(B) {3}
⎧
⎩
(C) ⎨ −3,
3⎫
⎬
2⎭
(D) {−3}
2. A função h, de domínio \ , definida por h( x ) = − 3 x 2 + 1 .
Seja t a recta tangente ao gráfico de h no ponto de abcissa
1
.
2
Qual é a inclinação da recta t?
(A) 150º
(B) 60º
(C) 120º
(D) − 60º
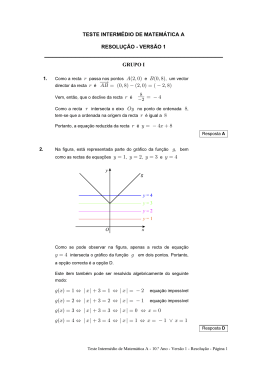
3. A função, f ´ , derivada da função f , tem a seguinte representação gráfica:
A representação gráfica da função f pode ser:
Internet: www.xkmat.pt.to
Página 1 de 4
4. A evolução das vendas de um produto, ao fim de t meses de publicidade por televisão, é dada em
percentagem de mercado, entre os produtos concorrentes, por
p(t ) = 50 −
45
,
t +1
t≥0.
Pode afirmar-se que:
(A) o produto só começou a ser vendido quando foi publicitado na televisão;
(B) as vendas podem atingir os sessenta pontos percentuais;
(C) o aumento médio da percentagem, nos três primeiros meses, foi de 11,25 pontos
percentuais ao mês;
(D) a função dada tem máximo igual a 50.
5. Apenas uma das seguintes rectas, é paralela a uma das rectas tangentes ao gráfico da função h,
definida em \ , por h( x ) = x 3 + x − 4 . Qual delas?
(B) y = −
(A) O eixo das abcissas
(C) y =
2
x +8
3
1
x+3
2
(D) y = x − 2
2ª PARTE
Apresente o seu raciocínio de forma clara, indicando os cálculos efectuados e as justificações necessárias.
Quando não é indicada a aproximação que se pede para um resultado, pretende-se o valor exacto.
]
[
1. Resolva, no intervalo −π , π , a seguinte equação trigonométrica:
π⎞
⎛
sen ⎜ x + ⎟ × ⎡3tg ( x ) + 3 ⎤ = 0
⎦
6⎠ ⎣
⎝
2. Sejam f e g funções, reais de variável real, definidas por f ( x ) = x 2 + x − 6 e
g ( x) =
4 − 2x
, de
x
domínios \ e \ \ {0} respectivamente.
2.1. Determine o domínio da função composta f o g e calcule
2.2. Caracterize a função
( f o g ) (4) .
g
, apresentando a expressão que a define simplificada.
f
2.3. Escreva uma equação da recta tangente ao gráfico de f no ponto de abcissa −1 .
2.4. Calcule, utilizando a definição de derivada de uma função num ponto, g '(2) .
2.5. Utilize a calculadora gráfica para determinar a abcissa do ponto do gráfico da função g
2
onde a recta tangente ao gráfico tem 45º de inclinação. Apresente o valor aproximado às
décimas. Na sua explicação, deve incluir o(s) gráfico(s) e as coordenadas dos pontos que
considerou para resolver esta questão.
Internet: www.xkmat.pt.to
Página 2 de 4
3. Na figura está representado um
referencial o.n. Oxyz.
Cada um dos pontos A, B e C pertence a
um eixo coordenado.
O ponto P pertence ao plano ABC.
O ponto P desloca-se no plano ABC, de
tal modo que é sempre vértice de uma
pirâmide quadrangular regular recta,
em que os restantes vértices, os da
base, pertencem ao plano xOy.
O plano ABC é definido pela equação:
x + 2 y + 3z = 9
(
)
3.1. Seja a a medida de comprimento de uma aresta da base a ∈ ]0,6[ .
Em função de a, indique as coordenadas do ponto P e mostre que o volume da pirâmide é
a3
dado por V ( a ) = a −
6
2
3.2. Estude a função V quanto à monotonia, sem recorrer à calculadora, e conclua qual é o
valor de a para o qual o volume da pirâmide é máximo.
3.3. Seja α um plano perpendicular ao plano ABC que contém o ponto C.
Determine uma equação cartesiana do plano α e indique quantas soluções existem?
FIM
Formulário
Regras de derivação
( ax )′ = a
k′ = 0 ( k ∈ \ )
bc
⎛ b ⎞′
⎜
⎟ =−
⎝ cx + d ⎠
(cx + d ) 2
(ax3 )′ = 3ax 2
(ax 2 )′ = 2ax
( mx + b )′ = m
( f + g )′ =
f ′ + g′
Cotações:
2ª Parte
1ª Parte
Questões
Pontos
Internet: www.xkmat.pt.to
10 pontos
cada
questão
1.
2.1.
2.2.
2.3.
2.4.
2.5.
3.1.
3.2.
3.3.
20
15
16
16
20
16
16
16
15
Página 3 de 4
Soluções
1ª Parte
1
D
2
C
3
C
4
C
5
D
2ª Parte
⎧ π 5π ⎫
, ⎬
⎩ 6 6 ⎭
1. S = ⎨ −
2.1. D f o g = \ \ {0}
2.2. D g = \ \ {−2,0,3}
f
( f o g ) (4) = −6
⎛g⎞
2
⎜ ⎟ ( x) = − 2
x + 3x
⎝ f ⎠
2.3. y = − x − 7
2.4. g '(2) = −1
2.5.
x ≈ −4,8
3.2. Crescente para a ∈ ]0,4] , Decrescente para a ∈ [ 4,6[ . Volume é máximo quando a = 4 .
3.3. Existem infinitas soluções por exemplo 2 x − y = 0
Internet: www.xkmat.pt.to
Página 4 de 4