Prof. MSc. HENRIQUE STARICK
•
•
•
•
•
•
•
GRADUAÇÃO :
Matemática (FAFITO)
Física ( UNIG)
POS GRADUAÇÃO
Matemática e Estatística (UFLA)
MESTRADO
Mestre Ciências Superiores (UMCC - Cuba)
FUNÇÃO
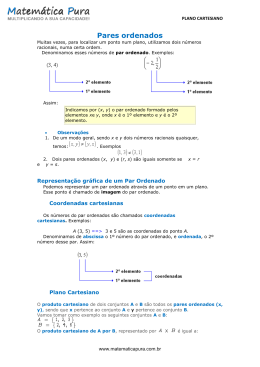
• RELAÇÃO: Dados dois conjuntos, A e B, não
vazios, definimos uma relação R de A em B
como um subconjunto de A x B; portanto R
está contido em A x B.
Considere A={0 ; 1} e B = {2 ; 3}.Temos:
A x B ={( 0 ; 2),(0 ; 3), (1; 2), (1 ; 3)}
• NOTAÇÃO: Podemos escrever uma relação de A em
B das seguintes formas:
• Nomeando seus pares ordenados;
R1 ={(0 ; 2),(0 ; 3),(1 ; 2), (1 ; 3)}
• Através de uma sentença matemática;
R2= {(x,y) Є A x B | y = x + 1}, onde cada conjunto é
representado A = {0 ; 1} B = {2 ; 3}.
• DOMÍNIO E IMAGEM DE UMA RELAÇÃO
Ao conjunto formado por todos os primeiros
elementos dos pares ordenados (x,y), de uma
Relação damos o nome de domínio e representamos
Por D(R).
Os segundos elementos desses pares formam o
conjunto do contra domínio CD(R).
Os elementos em que o primeiro conjunto faz relação
com os elementos do segundo conjunto, chamamos
de conjunto imagem, representado por Im(R).
•REPRESENTAÇÃO DE UMA RELAÇÃO
Podemos representar uma relação ou por um
diagrama de setas ou no plano cartesiano.
VEJAMOS UM EXEMPLO A SEGUIR.
Sendo A= {1 ; 2} e B = {3; 4; 5; 6},temos sua
representação no diagrama de setas. Dada a
função Y = x + 3, onde D ={1; 2}, CD ={3;4;5;6}
e Im = {4 ; 5}
•1
•2
•3
•4
•5
•6
EXERCITANDO:
SENDO R UMA RELAÇÃO POR R = {(x,y) Є IN* x IN* |y = 2x 10}, DETERMINE:
a) R
b) D(R)
c)Im(R)
d) gráfico de R
X
Y = 2X - 10
Y
1
2
Y = 2.1 – 10
Y = 2.2 - 10
-8
-6
3
Y = 2.3 - 10
-4
4
5
Y = 2.4 - 10
Y = 2.5 - 10
-2
0 não pertence a IN*
R = {(1;8),(2;6,(3;4),(4;2)}
D(R) = {1; 2; 3; 4}
Im(R) = {2; 4; 6; 8}
REPRESENTAÇÃO NO PLANO CARTESIANO
COORDENADAS
(1 ; 4) e (2 ; 5)
CONTRA DOMÍNIO Y
6
5
4
3
2
1
-2 -1 0
(2 ; 5)
(1 ; 4)
1
2
DOMÍNIO X
REPRESENTAÇÃO GRÁFICA
EIXO Y
10
9
8
7
6
5
4
3
2
1
0 1 2 3 4 5 6 7 8
EIXO X
FUNÇÃO - CONCEITO
• Dados conjuntos A e B, não vazios,
dizemos que a relação f de A em B é
função se, e somente se, para qualquer x
pertencente ao conjunto A existe, em
correspondência, um único (ЭI) y pertence a B
tal que o par ordenado (x,y) pertença a f.
• F é função de A em B <=>V x Є A, Э| Y Є B| (x; y) Є f
VEJAMOS ALGUNS EXEMPLOS DE FUNÇÃO
2.
3.
4.
1.
2.
3.
1.
2.
3.
4.
4.
3.
5.
6.
7.
1.
2.
3.
F1 é função porque todos os elementos
de A têm um único correspondente em B
F2 não é função porque 4ЄA, e não
têm correspondente em B.
F3 não é função porque 4ЄA e tem
Dois correspondentes em B
NOTAÇÃO E VALOR NUMÉRICO
NOTAÇÃO:
Podemos escrever uma função f: A B através de suas
variáveis X( independente) e Y(dependente). Exemplos:
• Y = 3x² + 4x ou f(x) = 3x² + 4x
• Y = 2x + 1 ou f(x) = 2x + 1
VALOR NUMÉRICO DE UMA FUNÇÃO
Chamamos de valor numérico de uma função o valor
Que a variável y = f(x) assume quando atribuímos a
a x um determinado valor. Vejamos:
F(x) = 3x² + 4x + 6, então f(2) = 3.2² + 4.2 + 6, f(2) =26
DOMÍNIO, IMÁGEM E CONTRADOMÍNIO
SEJA A FUNÇÃO F: A
A
-2.
-1.
0.
1.
B
.-2
.-1
.0
.1
.2
.3
B
R= {(-2;-1),(-1;0),(0;1),(1;2)}
Df = {-2 ; -1; 0; 1}
Imf = {-1 ;0; 1 ;2}
CDf = B ={-2; -1; 0; 1; 2; 3 }
Observação: decorre da definição que Im(f) está contido
No CD(f), Ou Im(f) está contido em B
GRÁFICO DE UMA FUNÇÃO
Para esboçar o gráfico de uma função no plano
Cartesiano, devemos atribuir valores a x,
determinando os respectivos valores numéricos
de Y.
Vejamos o exemplo de f: E F, definida por
Y = 2x, sendo E ={0; 1; 2}e F ={-4; -2; 0; 2; 4; }
x
y = 2x
y
-2
y = 2.(-2) -4
-1
y = 2.(-1) -2
0
y = 2. 0
0
1
y = 2.1
2
2
y = 2.2
4
Y
4
3
2
1
-2 -1 0
-1
-2
-3
-4
1
2
X
EXERCÍCIOS DE FIXAÇÃO
1- SENDO R UMA RELAÇÃO POR R= {(x,y) Є IN* x IN* |
X + 4 = Y}, DETERMINE:
a) R
b)D(R)
c)Im(R)
d) Cd(R)
e) Gráfico de R
2- SE Y = X + 1, e X < 6 / X Є IN*, CONSTRUA O
GRÁFICO DE R, IDENTIFICANDO SEU CAMPO DE
ATUAÇÃO, BEM COMO SEU DOMÍNIO, CONTRA
DOMÍNIO, IMÁGEM DE R.
OBS: OS EXERCÍCIOS DEVEM SER APRESENTADOS
AO PROFESSOR EM ESTRUTURA DIGITAL, PARA
QUE POSSAM SER VISUALIZADOS E DISCUTIDOS
POR TODA A EQUIPE.
RECONHECIMENTO DE UMA
FUNÇÃOATRAVÉS DO GRÁFICO
ANALIZANDO UM GRÁFICO DE UMA RELAÇÃO,
PODEMOS IDENTIFICAR SE ESTÁ É UMA FUNÇÃO OU
NÃO. PARA TAL É SÓ TRAÇAR PERPENDICULARES
AO EIXO X POR VALORES PERTENCENTES AO DOMÍNIO,
SE TODAS AS PERPENDICULARES INTERCEPTAREM O
GRÁFICO EM APENAS UM PONTO, ENTÃO ESSA RELAÇÃO
REPRESENTA POR ESSE GRÁFICO UMA FUNÇÃO.
OBSERVE:
ESSE GRÁFICO REPRESENTA
UMA FUNÇÃO, POIS TODAS AS
PERPENDICULARES AO EIXO X
INTERCEPTAM O GRÁFICO EM
APENAS UM SÓ PONTO.
Y
X
ESSE GRÁFICO NÃO REPRESENTA UMA FUNÇÃO,
POIS CADA PERPENDICULAR INTERCEPTA-O EM
DOIS PONTOS DISTINTOS.