UNIVERSIDADE SÃO FRANCISCO
ANTONIO MORANDIN JUNIOR
RA : 00200400206 – 10º Semestre
ANALISE DE ESTABILIDADE DE ATERRO REFORÇADO SOBRE SOLO MOLE
COM GEOGRELHAS
ITATIBA
2009
2
UNIVERSIDADE SÃO FRANCISCO
ANTONIO MORANDIN JUNIOR
RA : 00200400206 – 10º Semestre
ANALISE DE ESTABILIDADE DE ATERRO REFORÇADO SOBRE SOLO MOLE
COM GEOGRELHAS
Trabalho
apresentado
à
disciplina
Trabalho de Conclusão de Curso, do
Curso
de
Universidade
Engenharia
São
Civil
Francisco,
da
sob
orientação do Profª. Ms Cristina das
Graças Fassina Guedes, como exigência
parcial para conclusão do curso de
graduação.
.
ITATIBA
2009
3
DEDICATÓRIA
“Dedico este trabalho aos meus pais, que sempre
lutaram para que eu tivesse um futuro digno e me
ensinaram a nunca desistir de meus sonhos.”
4
AGRADECIMENTOS
A Deus por me mostrar que nada é impossível e por me guiar em todos os
momentos, principalmente nos de dificuldades.
Aos meus familiares que me atribuíram atenção e carinho para vencer essa
etapa da minha vida.
Ao professora e orientadora Ms Cristina das Graças Fassina Guedes, que fez
com que este trabalho de conclusão de curso se tornasse possível, se dedicando e
conduzindo da melhor maneira. Meus sinceros agradecimentos.
Aos funcionários da Maccaferri do Brasil Ltda. que contribuiu com
informações referentes à pesquisa.
Ao corpo docente da Engenharia Civil que contribuiu com os ensinamentos e
crescimento profissional.
5
MORANDIN JUNIOR, A. Analise de estabilidade de aterro reforçado sobre
solo mole. 2009. Faculdade de Engenharia Civil, Universidade São Francisco,
Itatiba, 2009.
RESUMO
Este setor, denominado de Engenharia Geotécnica, se ocupa primordialmente
de projetos de fundações de edifícios e obras de arte, contenções, taludes e sua
estabilização, projetos de terraplanagem, pavimentação e drenagem, além de túneis
e barragens.
Em muitos casos é comum, ao se realizar uma investigação geotécnica, a
presença de solos com baixa capacidade de suporte, e mediante a incidência cada
vez maior de casos como este e a eminente necessidade de vencer-los, a
solicitação por profissionais qualificados para trabalhar com esse tipo de situação,
vem crescendo gradativamente.
Visando uma situação de um empreendimento que requer a utilização de tal
solução, com o intuito de vencer situações de solos com baixa capacidade de
suporte, tomado por base a Norma BS 8006 (Principal norma de projetos
geotécnicos utilizando geossintéticos ) este trabalho tem como objetivo descrever as
principais metodologias de analise de estabilidade para um aterro Reforçado com
geogrelhas sobre solo mole, sendo este estaqueado ou não, assim como as
principais investigações geotécnicas, afim de se obter as informações necessárias
para a aplicação de tais conceitos.
PALAVRAS CHAVES: Solo Reforçado, Dimensionamento e Geossintético.
6
MORANDIN JUNIOR, A. Analise de estabilidade de aterro reforçado sobre
solo mole. 2009. Faculdade de Engenharia Civil, Universidade São Francisco,
Itatiba, 2009.
ABSTRACT
This sector, denominated of Geotecnical Engineering, occupies mostly of
buildings and works of art foundations projects, contentions, slopes and your
stabilization, embankment projects, paving and drainage, beyond tunnels and dams.
In lots of cases is common, to the if accomplish an geotechnical investigation,
the presence of soils with support low capacity, and by means of the every time
larger incidence of cases as this and the eminent need to win them, the solicitation
for professionals qualified to work with that kind of situation, it comes growing
gradually.
Aiming a situation of an enterprise that requires the utilization of such a
solution, with objective of wining soils situations with support low capacity, taken by
base Norma BS 8006 (Geotecnical Projects main norm using geosynthetics) this
work has as goal describe the main methodologies of analyzes of stability for an
earthwork Reinforced with geogrids about soft soil, being this with stakes or not, as
well as the main geotechnical investigations, similar to obtain the necessary
information for the application of such concepts.
KEY WORDS: Reinforced Soil, Measure, Geosynthetics
7
INDICE DE FIGURAS
FIGURA 1 – CICLO DE QUALIDADE PARA PROJETOS GEOTÉCNICOS SEGUNDO A ABEG .............. 18
FIGURA 2- ILUSTRAÇÃO DO ENSAIO SPT ................................................................................. 22
FIGURA 3 - ILUSTRAÇÃO DO PIEZOCONE ................................................................................. 26
FIGURA 4 - EQUIPAMENTOS UTILIZADOS PARA A REALIZAÇÃO DO ENSAIO CPT E CPTU. ............. 27
FIGURA 5 - RESULTADOS TÍPICOS DE UM ENSAIO DE CONE ...................................................... 28
FIGURA 6 - EQUIPAMENTO PARA ENSAIO DE PALHETA “IN SITU” ................................................ 34
FIGURA 7 - EQUIPAMENTO PARA ENSAIO DE PALHETA .............................................................. 35
FIGURA 8 - CURVAS TÍPICAS TORQUE X ÂNGULO DE ROTAÇÃO EM ENSAIOS DE PALHETA. ............ 36
FIGURA 9 – CILINDRO PADRÃO PARA REALIZAÇÃO DO ENSAIO DE PROCTOR ............................. 39
FIGURA 10 - CURVA OBTIDA EM ENSAIO DE COMPACTAÇÃO PROCTOR NORMAL. ........................ 41
FIGURA 11 - CURVAS DE COMPACTAÇÃO DE UM SOLO COM DIFERENTES ENERGIAS.................... 42
FIGURA 12 - CURVAS DE COMPACTAÇÃO NORMAL DE ALGUNS SOLOS BRASILEIROS................... 43
FIGURA 13 - PRENSA DE COMPRESSÃO EDOMÉTRICA.............................................................. 45
FIGURA 14 - ESQUEMA DA CÂMARA DE ENSAIO DE COMPRESSÃO EDOMÉTRICA. ........................ 46
FIGURA 15 - CURVA DE COMPRESSÃO EDOMÉTRICA DE UMA ARGILA MOLE. .............................. 48
FIGURA 16 - CONSTRUÇÃO GRÁFICA PARA A DETERMINAÇÃO DA TENSÃO DE PRÉ-ADENSAMENTO.
..................................................................................................................................... 49
FIGURA 17 - CONSTRUÇÃO GRÁFICA PARA A DETERMINAÇÃO DA TENSÃO DE PRÉ-ADENSAMENTO.
..................................................................................................................................... 50
FIGURA 18 - CURVA DE RECALQUE NA ESCALA DA RAIZ DO TEMPO PARA A DETERMINAÇÃO DE CV53
FIGURA 19 - CURVA DE RECALQUE, MÉTODO DO LOGARITMO DO TEMPO.................................... 54
FIGURA 20 - ESQUEMA DO EQUIPAMENTO DE CISALHAMENTO DIRETO. ...................................... 55
FIGURA 21 - RESULTADO TÍPICO DE UM ENSAIO DE CISALHAMENTO DIRETO. .............................. 56
FIGURA 22 - ENVOLTÓRIA DE RESISTÊNCIA. ............................................................................ 57
FIGURA 23 - APARELHO DE COMPRESSÃO TRIAXIAL ................................................................. 58
FIGURA 24 - APLICAÇÃO DA TENSÃO PRINCIPAL Σ1 E DA TENSÃO DE CONFINAMENTO Σ3; (B) CORPO
DE PROVA ROMPIDO; (C) CIRCULOS DE MOHR E ENVOLTÓRIA DE COULOMB. ...................... 59
FIGURA 25 - ELEMENTOS COMPONENTES DE UMA GEOGRELHA. ................................................ 63
FIGURA 26 - MONÔMEROS DOS PRINCIPAIS POLÍMEROS DOS GEOSSINTÉTICOS. ......................... 64
FIGURA 27 - COMPORTAMENTO TENSÃO VS DEFORMAÇÃO DE DIFERENTES POLÍMEROS............ 66
FIGURA 28 - ESQUEMA ILUSTRATIVO DOS ENSAIOS DE CISALHAMENTO DIRETO E DE
ARRANCAMENTO ............................................................................................................ 67
FIGURA 29 - DIAGRAMA ESQUEMÁTICO DO EQUIPAMENTO APSR .............................................. 68
FIGURA 30- ESQUEMA ILUSTRATIVO DO ENSAIO DE CISALHAMENTO DIRETO COM REFORÇO
INCLINADO ..................................................................................................................... 69
8
FIGURA 31 - ESQUEMA DO ENSAIO DE TRAÇÃO CONFINADA COM SOLO ...................................... 70
FIGURA 32 - ELEMENTOS DE SOLO COM E SEM REFORÇO ....................................................... 71
FIGURA 33 - ESTADO LIMITE ULTIMO PARA A BASE O ATERRO REFORÇADO ................................ 72
FIGURA 34 – ESTADO LIMITE DE UTILIZAÇÃO ( SERVICIBILIDADE ) PARA ATERROS COM BASE
REFORÇADO. ................................................................................................................. 73
FIGURA 35 - REFORÇO UTILIZADO PARA CONTROLAR SOMENTE A ESTABILIDADE INICIAL DO
ATERRO......................................................................................................................... 75
FIGURA 36 - REFORÇOS UTILIZADOS PARA CONTROLE SOMENTE DE ESTABILIDADE INICIAL E
RECALQUE DO ATERRO. .................................................................................................. 75
FIGURA 37- PROCEDIMENTO PARA AVALIAR A ESTABILIDADE ROTACIONAL ATRAVÉS DE ANÁLISES
DE SUPERFICIES CIRCULARES DE DESLIZAMENTO. ............................................................ 87
FIGURA 38 - ESTABILIDADE LATERAL NA INTERFACE DO ATERRO. ............................................. 89
FIGURA 39 - ANALISE DE ESTABILIDADE CONTRA A EXPULSÃO DO SOLO DE FUNDAÇÃO. ....... ERRO!
INDICADOR NÃO DEFINIDO.
FIGURA 40 – METODO DE MEYERHOF PARA ESTABELECER SUPERFÍCIE CRITICA DE RUPTURA DE
FUNDAÇÃO .................................................................................................................... 94
FIGURA 41 – MÉTODO DAS LAMELAS ....................................................................................... 95
FIGURA 42 – LAMELA DE FORMA INDIVIDUAL ............................................................................ 96
FIGURA 43 – FORÇAS ATUANTES EM UMA LAMELA SEGUNDO O MÉTODO DE BISHOP SIMPLIFICADO.
..................................................................................................................................... 97
FIGURA 44 – CURVA DE ADENSAMENTO ................................................................................ 100
FIGURA 45 - CONFIGURAÇÕES DE ATERROS ESTAQUEADOS. .................................................. 102
FIGURA 46 - ESTADO LIMITE ULTIMO PARA ATERROS ESTAQUEADOS COM BASE REFORÇADA. ... 104
FIGURA 47 - ESTADO LIMITE DE SERVICIBILIDADE (UTILIZAÇÃO) PARA ATERROS ESTAQUEADOS COM
REFORÇO DE BASE. ...................................................................................................... 105
FIGURA 48 - LIMITE DOS CAPTEIS. ......................................................................................... 107
FIGURA 49 - VARIÁVEIS USADAS NA DETERMINAÇÃO DE TRP. ................................................. 110
FIGURA 50 - ESTABILIDADE LATERAL CONTRA O DESLIZAMENTO NA INTERFACE ATERRO /
REFORÇO. ................................................................................................................... 112
FIGURA 51 - VARIÁVEIS UTILIZADAS NA ANALISE DE ESTABILIDADE GLOBAL EM ATERROS
ESTAQUEADOS COM REFORÇO DE BASE......................................................................... 115
9
INDICE DE TABELAS
TABELA 1 - CONSISTÊNCIA E COMPACIDADE DE SOLOS ARGILOSOS E ARENOSOS ...................... 23
TABELA 2 - PARAMETROS MÉDIOS DOS SOLOS ......................................................................... 24
TABELA 3 - PARÂMETROS ESTIMADOS ATRAVÉS DO ENSAIO DE PIEZOCONE ............................... 25
TABELA 4 - FATOR TEMPO T* PARA ANÁLISE DOS ENSAIOS DE DISSIPAÇÃO ................................ 30
TABELA 5 - SENSIBILIDADE DAS ARGILAS ................................................................................. 37
TABELA 6 - ENERGIAS DE COMPACTAÇÃO ................................................................................ 41
TABELA 7 - TIPOS DE GEOSSINTÉTICOS E SUAS PRINCIPAIS APLICAÇÕES ................................... 62
TABELA 8 - PROPRIEDADES DE DEGRADAÇÃO DOS PRINCIPAIS POLÍMEROS QUE CONSTITUEM AS
GEOGRELHAS ................................................................................................................ 65
TABELA 9 - RESUMO DOS FATORES PARCIAIS DE SEGURANÇA PARA SEREM UTILIZADOS EM
PROJETOS DE ATERROS REFORÇADOS SOBRE SOLO MOLE................................................ 76
TABELA 10 - FATORES DE REDUÇÃO EM FUNÇÃO DO TIPO DE POLÍMERO .................................. 79
TABELA 11 - FAIXA DE FATORES DE DANO PARA GEOGRELHAS ................................................ 82
TABELA 12 - CRITÉRIO PARA CLASSIFICAÇÃO DA CAPACIDADE DE SOBREVIVÊNCIA DE
GEOSSINTÉTICOS .......................................................................................................... 83
TABELA 13 - CLASSIFICAÇÃO DA SEVERIDADE DO MEIO ........................................................... 83
TABELA 14 – FATOR TEMPO EM FUNÇÃO DA PORCENTAGEM DE RECALQUE PARA ADENSAMENTO
PELA TEORIA DE
TERZAGHI ........................................................................................... 100
TABELA 15 – COEFICIENTE DE ARQUEAMENTO CC PARA REFORÇO DE ATERROS ESTAQUEADOS 108
10
LISTA DE ABREVIATUTAS, SIGLAS E SIMBOLOS
ABEG = Associação Brasileira de Empresas de Projeto e Consultoria em
Engenharia Geotécnica
SPT = Standard Penetration Test
NSPT = Number Standard Penetration Test
CPT = Cone Penetration Test
CPTU = Penetration Test
= resistência de ponta do cone
= atrito lateral
OCR = Razão
de pré-adensamento
= Resistência não drenada
Eu = Módulo de Young não drenado
M = Módulo edométrico
Gmax = Módulo cisalhante máximo
Sf = Sensitividade
= Coeficiente de adensamento horizontal
= Coeficiente de adensamento vertical
ko = Coeficiente de empuxo no repouso
φ = Ângulo de atrito efetivo
= Densidade relativa ()
= raio do piezocone;
= tempo de dissipação;
= índice de rigidez;
T* = fator tempo
G = módulo de cisalhamento do solo.
= tensão vertical in situ;
= poropressão medida na face do cone;
= poropressão medida na base do cone;
= poropressão hidrostática.
11
= módulo de deformabilidade correspondente a 25% da tensão
desviadora máxima.
IPT = Instituto de Pesquisas Tecnológicas
ABNT = Associação Brasileira de Normas Técnicas ()
M = torque máximo
D = diâmetro da palheta
= sensibilidade da argila
= Peso específico seco do solo
γ = peso específico aparente seco do solo
γ = peso específico real dos grãos do solo
γ = peso específico da água
S = grau de saturação;
w = teor de umidade
= energia de compactação por unidade de volume;
= peso do soquete
ℎ = altura de queda do soquete;
= número de golpes por camada;
! = número de camadas;
" = volume do solo compactado.
′$ = pressão de pré-adensamento
%= índice de vazios
GG = Geogrelhas (geogrid - genérica)
GGE = Geogrelha Extrudada (extruded geogrid)
GGB = Geogrelha Ligada (bounded geogrid)
GGW = Geogrelha Tecida (woven geogrid)
PET = poliéster
PP = polipropileno
PE = polietileno
PEAD = polietileno de alta densidade
APSR = Automated Plane Strain Reinforcement cell
&' = resistência de projeto do reforço;
( = fator parcial para ramificações econômicas de colapso
12
$)) = fator parcial do material relativo a consistência de fabricação do reforço
$) = fator parcial do material relativo a extrapolação dos ensaios
procedendo com a resistência de base.
$) = fator parcial do material relativo a susceptibilidade do reforço a danos
de instalação.
$ = fator parcial do material relativo ao ambiente no qual o reforço é
instalado.
* = Fator de redução devido a deformações por fluência
+ = Fator de redução devido à degradação química e biológica pelo meio
ambiente
, = Fator de redução devido a eventuais emendas
' = Fator de redução devido a danos mecânicos
&- = Propriedade funcional da geogrelha
&. = Propriedade índice da geogrelha
= fator de redução total
H = altura total do aterro;
/ = comprimento horizontal do talude lateral do aterro;
$ = fator parcial de segurança para o um geossintético
Yj = braço do momento vertical para a superfície ao longo da base do aterro
MRRj = máximo momento resistente devido ao reforço em um local jao longo
da base do aterro;
MDj = máximo momento atuante fatorado em um local ao longo da base do
aterro
MRSj = máximo momento resistente fatorado devido ao solo em um local ao
longo da base do aterro.
fn = fator de segurança parcial que governa as ramificações econômicas do
mecanismo de falha
fp = fator de segurança parcial aplicado à resistência do reforço ao pull-out
(arrancamento)
Troj = carga no reforço por metro, necessária para manter a estabilidade no
ponto ao longo da base do aterro;
γ = peso específico do material que forma o aterro;
h = altura média do aterro sobre o reforço ao longo do comprimento
13
α = coeficiente de interação solo/ângulo de adesão do reforço
Lj = comprimento de ancoragem necessário para o reforço, por metro, dentro
do arco que define a superfície de ruptura;
Cu = resistência não drenada do solo mole que forma a fundação adjacente
ao reforço.
Tds = carga de tração no reforço por metro, necessária para resistir ao empuxo
lateral gerado pelo aterro;
Ka = coeficiente de empuxo ativo
ωs = intensidade da sobrecarga externa no topo do talude;
ffs = fator parcial de segurança para o peso específico do solo
fq = fator de segurança parcial para as cargas externas aplicadas
fs = fator de segurança parcial para a resistência ao deslizamento do reforço
Rha = força horizontal fatorada que causa a expulsão do solo de fundação
Rhp = força horizontal fatorada devida à resistência passiva do solo de
fundação
Rs = força horizontal fatorada devida à resistência ao cisalhamento do solo de
fundação
RR = força horizontal fatorada devida à resistência ao cisalhamento do solo de
fundação no lado inferior do reforço
ffs = fator parcial de segurança para o peso específico do solo
E = Empuxo
X = Esforço cisalhante
N = Força normal
T =
A força que mede a resistência mobilizada, que é uma fração da
ℓ = É o comprimento da base da lamela
F = Coeficiente de segurança referente à relação entre a resistência ao
cisalhamento do solo e a tensão cisalhante atuante
C2 = Índice de recompressão
C3 = Índice de Compressão
P5 = Tensão de Pré-adensamento
σ7 = Tensão inicial
σ8 = Tensão após a construção do aterro
= Tempo em que ocorrerá o Recalque
14
& = Fator tempo, em função do grau de adensamento
9' = Altura referente a metade da espessura da camada de solo mole
U = Grau de adensamento ao longo da profundidade
TD = resistência de projeto para o reforço
fn = fator parcial que rege as ramificações econômicas de uma possivel falha
Qp = capacidade de carga admissível de cada estaca que forma o grupo
ffs = fator parcial de segurança para o peso específico do solo
n = inclinação do talude do aterro na forma n-horizontal/1vertical
WT = carga vertical distribuída atuando no reforço entre os capitéis de estacas
adjacentes
ffs = fator parcial de segurança para o peso específico do solo
fq = fator de segurança parcial para as cargas externas aplicadas
ε = deformação do reforço
Tds = carga de tração no reforço por metro, necessária para resistir ao empuxo
lateral gerado pelo aterro;
MD = momento solicitante em todos os pontos ao longo da base do aterro
MRS = momento resistente devido ao solo em todos os pontos ao longo da
base do aterro
MRP = momento resistente devido às estacas em todos os pontos ao longo da
base do aterro
MRR = momento resistente devido ao reforço em todos os pontos ao longo da
base do aterro
15
SUMÁRIO
1.
INTRODUÇÃO ............................................................................................................. 17
2.
INVESTIGAÇÃO GEOTÉCNICA ................................................................................. 21
2.1.
GENERALIDADES ............................................................................................... 21
2.2.
ENSAIOS DE CAMPO .......................................................................................... 21
2.2.1. SONDAGENS DE SIMPLES RECONHECIMENTO - SPT ............................... 21
2.2.2. ENSAIO DE CONE (CPT) E DE PIEZOCONE (CPTU) .................................... 25
2.2.2.1.
GENERALIDADES ........................................................................................... 25
2.2.2.2.
SOLOS ARGILOSOS ............................................................................... 28
2.2.2.2.1. RESISTÊNCIA NÃO-DRENADA (Su) ................................................... 28
2.2.2.2.2. COEFICIENTE DE ADENSAMENTO HORIZONTAL (ℎ) DO SOLO ... 29
2.2.2.3.
SOLOS ARENOSOS ................................................................................ 31
2.2.2.3.1. DENSIDADE RELATIVA ....................................................................... 31
2.2.2.3.2. ÂNGULO DE ATRITO INTERNO DO SOLO (φ’)................................... 31
2.2.2.3.3. MÓDULO DE DEFORMABILIDADE (E) ............................................... 32
2.2.3. ENSAIOS DE PALHETA (“VANE TEST”) ......................................................... 32
2.3.
ENSAIOS DE LABORATORIO ............................................................................. 37
2.3.1. GENERALIDADES ........................................................................................... 37
2.3.2. ENSAIOS DE COMPACTAÇÃO DE PROCTOR .............................................. 38
2.3.3. ENSAIO DE COMPRESSÃO EDOMÉTRICA ................................................... 44
2.3.3.1.
GENERALIDADES ................................................................................... 44
2.3.3.2.
ENSAIO DE COMPRESSÃO COM CARREGAMENTO INCREMENTAL . 44
2.3.3.3.
MÉTODO DE CASAGRANDE .................................................................. 48
2.3.3.4.
MÉTODO DE PACHECO SILVA............................................................... 49
2.3.3.5.
DETERMINAÇÃO DO COEFICIENTE DE ADENSAMENTO .................... 50
2.3.3.6.
MÉTODO DE TAYLOR ............................................................................. 52
2.3.4. ENSAIO DE CISALHAMENTO DIRETO ........................................................... 54
2.3.5. ENSAIO DE COMPRESSÃO TRIAXIAL ........................................................... 57
3.
GEOSSINTÉTICOS ..................................................................................................... 61
3.1.
GENERALIDADES ............................................................................................... 61
16
3.2.
4.
GEOGRELHA....................................................................................................... 62
PROJETO DE ATERRO REFORÇADO SOBRE SOLO MOLE ................................... 71
4.1.
GENERALIDADES ............................................................................................... 71
4.2.
FATORES PARCIAIS ........................................................................................... 76
4.2.1. ASPECTOS RELATIVOS AOS REFORÇOS – FATORES DE REDUÇÃO....... 77
4.2.1. FATOR DE REDUÇÃO DEVIDO A FLUÊNCIA ................................................ 79
4.2.2. FATOR DE REDUÇÃO DEVIDO A DEGRADAÇÃO PELO MEIO AMBIENTE . 80
4.2.3. FATOR DE REDUÇÃO DEVIDO A EMENDAS ................................................ 81
4.2.4. FATOR DE REDUÇÃO DEVIDO A DANOS MECANICOS ............................... 81
4.3.
ESTABILIDADE LOCAL ....................................................................................... 84
4.4.
ANÁLISE DE SUPERFÍCIES DE DESLIZAMENTO ............................................. 84
4.5.
DESLIZAMENTO LATERAL ................................................................................. 88
4.6.
EXPULSÃO DA FUNDAÇÃO ............................................................................... 89
4.7.
ESTABILIDADE GLOBAL .................................................................................... 94
4.2.2. METODO DE BISHOP SIMPLIFICADO ........................................................... 97
4.8.
VERIFICAÇÃO DO RECALQUE .......................................................................... 98
4.9.
REFORÇO USADOS COMO COMPONENTES PARA O CONTROLE DA
ESTABILIDADE E RECALQUE DO ATERRO ............................................................... 101
4.9.2. CAPACIDADE DE UM GRUPO DE ESTACAS............................................... 104
4.9.3. GRUPO DE ESTACAS EXTENDIDO ............................................................. 106
4.9.4. DISTRIBUIÇÃO DAS CARGAS VERTICAIS .................................................. 107
4.9.5. ESCORREGAMENTO LATERAL ................................................................... 111
4.9.6.
ANCORAGEM DO REFORÇO ................................................................... 112
4.9.7. ESTABILIDADE GLOBAL............................................................................... 114
4.9.8. DEFORMAÇÃO NO REFORÇO ..................................................................... 115
5.
CONCLUSÃO ............................................................................................................ 116
6.
REFERÊNCIAS BIBIOGRÁFICAS ............................................................................ 118
Formatado: Fonte: 12 pt
17
1. INTRODUÇÃO
Ao se realizar uma investigação geotécnica em locais propícios a construção
de obras de infra-estrutura, é fato comum se deparar com a presença de camadas
de solos com baixa capacidade de suporte, solos totais ou parcialmente saturados,
os chamados solos moles. Esses solos ao serem carregados sofrem um nível de
compressibilidade que induzem ao seu adensamento. De maneira muito simples,
adensamento nada mais é que a retirada da água existente nos vazios do solo,
esses solos por sua vez apresentam baixa resistência ao cisalhamento que, durante
o processo de adensamento, conduz a um estado de tensões tal que pode levá-los a
ruptura.
Devido situações como estas, citadas no parágrafo anterior, e a necessidade
cada vez maior de vencer-las, nas últimas décadas vem-se percebendo um rápido
crescimento na demanda dos geossintéticos nos mercados mundial e nacional. Esse
fato induz simultaneamente um esforço continuo dos pesquisadores para adequar as
potencialidades destes novos materiais e necessidades do mercado consumidor.
Para tal vem se desenvolvendo esforço no sentido de caracterizar as propriedades
destes materiais, de se adequar ensaios as finalidades a que se destinam e de
elaborar métodos de dimensionamento que consideram as características de obras
e dos materiais utilizados.
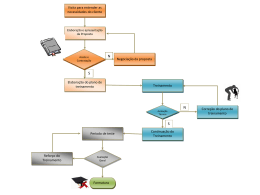
Tomando por base o Ciclo de qualidade de Projetos Geotécnicos da ABEG (
Figura 1) – Associação Brasileira de Empresas de Projeto e Consultoria em
Engenharia Geotécnica, onde temos como principais etapas de um projeto
geotécnico:
18
Figura 1 – Ciclo de qualidade para projetos Geotécnicos segundo a ABEG
Fonte: ( http://www.abeg.com.br )
1 - Necessidades dos Clientes:
Caracterização do empreendimento face aspectos geotécnicos;
2 - Coleta de dados:
Conhecimento do comportamento geotécnico dos solos;
Acompanhamento de ensaios in situ ou em laboratórios;
3 - Análise dos dados:
Definição dos parâmetros geotécnicos envolvidos;
4 - Elaboração do projeto:
Conceituação dos fenômenos e inteirações envolvidas;
Seleção dos modelos de cálculo;
Dimensionamento dos elementos;
19
Especificação, memorial e desenhos;
Seqüência executiva;
5 - Acompanhamento da execução da obra (ATO):
Garantia da execução do projetado;
Adequação do projeto às condições de execução no campo;
6 - Avaliação do desempenho:
Monitoramento das obras;
Visando uma situação de um empreendimento que requer a utilização de tal
solução, com base na Norma BS 8006 (Principal norma de projetos geotécnicos
utilizando geossintéticos ) será descrito as principais metodologias de analise de
estabilidade para um aterro Reforçado com geogrelhas sobre solo mole, sendo este
estaqueado ou não, assim como as principais investigações geotécnicas, afim de se
obter as informações necessárias para a aplicação de tais conceitos.
A analise de estabilidade de um aterro reforçado sobre solos moles é
governada principalmente pela resistência ao cisalhamento do solo de fundação, ou
o solo que está imediatamente em contato com a base do aterro, onde em geral os
problemas na construção dos aterros compactados sobre solos moles são
essencialmente causados pela baixa capacidade de suporte da fundação, que ao
ser solicitado ao cisalhamento não encontra suficiente resistência e rompe, sendo
necessária à adição de um reforço geossintético na base desse aterro a fim de
estabilizá-lo.
Os critérios estabelecidos pela BS 8006, sendo governados pela tensão
cisalhante do solo de fundação e aos problemas de capacidade de suporte, são:
Os estados limites últimos considerados segundo a BS 8006 são:
a) Estabilidade local do material de aterro;
b) Estabilidade rotacional do material de aterro;
c) Estabilidade de deslizamento lateral do material de aterro;
d) Estabilidade de extrusão da fundação;
e) Estabilidade global.
20
Os estados limites de servicibilidade a serem considerados são:
a) Tensão excessiva no reforço;
b) Recalque da fundação.
A eminente necessidade de vencer situações de solos com baixa capacidade
de suporte, sobretudo em obras de infra-estrutura, conseqüentemente faz crescer a
solicitação por profissionais qualificados para trabalhar com esse tipo de situação.
Por isso, procura-se através desta pesquisa contribuir com a engenharia, revisando
bibliograficamente os conhecimentos referentes a analise de estabilidade de um
aterro reforçado sobre solo mole com geogrelha.
21
2. INVESTIGAÇÃO GEOTÉCNICA
2.1.
GENERALIDADES
Formatado: Nível 2
A aplicação da teoria da Mecânica dos Solos aos problemas de engenharia,
exige o conhecimento de parâmetros que representem determinadas propriedades
dos solos. A determinação destes parâmetros pode ser realizada através de ensaios
de laboratório, ou ensaios realizados “in situ”, onde estas devem ser devidamente
programadas e executadas com rígidos critérios, sob a pena de insucesso nas
fases de projeto e fatalmente na fase de execução e operação.
2.2.
ENSAIOS DE CAMPO
2.2.1. SONDAGENS DE SIMPLES RECONHECIMENTO - SPT
O Standard Penetration Test (SPT), é reconhecidamente a mais popular,
rotineira e econômica ferramenta de investigação em praticamente todo o mundo.
Esta sondagem é um procedimento geotécnico que constitui uma medida de
resistência dinâmica conjugado ao objetivo de identificar a estratigrafia do subsolo,
sendo composta pó duas fases que se intercalam: perfuração e amostragem.
A perfuração é realizada com um trado até se atingir o nível freático, e com
um trépano e jato d’água no solo situado abaixo do nível freático. A amostragem é
executada a cada metro de profundidade, por processo de cravação dinâmica ou
percussão, e está associada ao ensaio de penetração padronizado (SPT- “Standard
Penetration Test”). Este ensaio permite uma estimativa da resistência do solo,
através da dificuldade ou facilidade de cravação do amostrador ao longo da
profundidade.
Ao se realizar uma sondagem, pretende-se conhecer o tipo de solo perfurado
( através da retirada de amostras deformadas, a cada metro de profundidade ), a
resistência do solo à cravação do amostrador padrão, e o posicionamento do nível
d’água.
O ensaio SPT tem sido usado para inúmeras aplicações. Dentre elas, pode-se
citar: identificação do perfil geotécnico, previsão da tensão admissível de fundações
Formatado: Nível 2
Formatado: Nível 3
22
diretas em solos granulares, identificação da consistência de solos coesivos e
rochas brandas, e indicação da densidade relativa de solos granulares.
O ensaio consiste basicamente na cravação de um amostrador padrão no
solo, através da queda livre de um peso de 65kg (martelo) caindo de uma altura de
75cm. A perfuração é realizada por tradagem e circulação de água, utilizando-se um
trépano de lavagem como ferramenta de escavação. A Figura 2 ilustra o ensaio
SPT.
Figura 2- Ilustração do Ensaio SPT
Fonte: (Maccaferri).
23
Nos ensaios SPT, o dado registrado é o número de golpes (NSPT) necessário
para que o amostrador padronizado penetre 30 cm no solo, após uma penetração
inicial de 15 cm.
Os valores de NSPT são usualmente obtidos a cada metro de sondagem e
representados em um gráfico em função da profundidade.
A caracterização do tipo de solo de cada camada é feita com base no exame
táctil-visual do material recolhido durante as operações de cravação dos
amostradores padronizados.
A partir do conhecimento do tipo de solo e do valor de NSPT, podem-se
estimar, com base em correlações empíricas, as principais características de
densidade, consistência, deformabilidade e resistência das camadas de solo.
Tabela 1 - Consistência e Compacidade de solos argilosos e arenosos
Fonte: ( Joppert, 2001).
Solo
NSPT
Designação
Argilas e siltes argilosos
<2
3–4
5–8
9 – 15
16 – 30
>30
Muito mole
Mole
Média
Rija
Muito rija
dura
Areias e siltes arenosos
<4
5 – 10
11 – 30
31 – 50
> 50
Fofo
Pouco compacto
Medianamente compacto
Compacto
Muito compacto
24
Tipo de
Faixa
Solo
de SPT
0-4
Tabela 2 - Parametros médios dos solos
Fonte : ( Joppert, 2001)
Peso Especifico
Ângulo
Modulo de
de atrito
elasticidade Natural Saturado
efetivo
(t/m²)
(t/m³)
(t/m³)
(f)
2000 - 5000
1,7
1,8
25°
Coesão
efetiva
(t/m²)
-
Areia pouco
5-8
4000 - 8000
1,8
1,9
30°
-
siltosa/pouco
9 - 18
5000 - 10000
1,9
2,0
32°
-
argilosa
19 - 41
8000 - 15000
2,0
2,1
35°
-
Areia média
≥ 41
16000 - 20000
2,0
2,1
38°
-
0–4
2000
1,7
1,8
25°
0
5–8
4000
1,8
1,9
28°
0,5
e fina muito
argilosa
Argila
9 - 18
5000
1,9
2,0
30°
0,75
19 – 41
10000
2,0
2,1
32°
1,0
0–2
200 – 500
1,5
1,7
20°
0,75
porosa
3–5
500 – 1000
1,6
1,7
23°
1,5
vermelha e
6 – 10
1000 – 2000
1,7
1,8
25°
3,0
≥ 10
2000 – 3000
1,8
1,9
25°
3,0 a 7,0
0–2
100
1,7
1,8
20°
0,75
amarela
3–5
100 – 250
1,8
1,9
23°
1,5
pouco
6 – 10
250 – 500
1,9
1,9
24°
2,0
arenosa
11 – 19
500 – 1000
1,9
1,9
24°
3,0
20 – 30
3000 – 10000
2,0
2,0
25°
4,0
≥ 30
10000 – 15000
2,0
2,0
25°
5,0
0–2
500
1,5
1,7
15°
1,0
Argila siltosa
(terciário)
Argila
3–5
500 – 1500
1,7
1,8
15°
2,0
arenosa
6 – 10
1500 – 2000
1,8
1,9
18°
3,5
pouco siltosa
11 – 19
2000 – 3500
1,9
1,9
20°
5,0
≥ 20
3500 – 5000
2,0
2,0
25°
6,5
Turfa / argila
0–1
40 – 100
1,1
1,1
15°
0,5
orgânica
2–5
100 – 150
1,2
1,2
15°
1,0
5-8
8000
1,8
1,9
25°
1,5
pouco
9 - 18
1000
1,9
2,0
26°
2,0
argiloso
19 - 41
15000
2,0
2,0
27°
3,0
≥ 41
20000
2,1
2,1
28°
5,0
Silte arenoso
(residual)
25
2.2.2. ENSAIO DE CONE (CPT) E DE PIEZOCONE (CPTU)
2.2.2.1.
GENERALIDADES
Formatado: Nível 3
Formatado: Nível 2
Os ensaios de cone, executados com monitoramento mecânico ou elétrico,
são conhecidos internacionalmente há várias décadas como “Cone Penetration
Test”, com a sigla CPT, sendo este utilizado no Brasil a desde o final da década de
1950. O ensaio consiste na cravação estática de uma haste cilíndrica com ponta em
forma cônica, medindo-se a resistência de ponta ( ) e o atrito lateral ( ).
Mais recentemente, foi desenvolvido o Ensaio de Piezocone (CPTU), que
utiliza um transdutor piezométrico na ponta cônica. No ensaio de Piezocone, obtémse, portanto, o registro das poropressões durante a cravação do cone, além das
medições usuais do ensaio de CPT .
Os ensaios de cone e piezocone , vêm se caracterizando internacionalmente
como uma das mais importantes ferramentas de prospecção geotécnica. Resultados
de ensaios podem ser utilizados para determinação estratigráfica de perfis de solos,
determinação de propriedades dos materiais prospectados, particularmente em
depósitos de argilas moles, e previsão da capacidade de carga de fundações. A
Tabela 3 apresenta os principais parâmetros que são usualmente estimados através
do ensaio de piezocone.
Tabela 3 - Parâmetros estimados através do ensaio de Piezocone
Fonte : ( Joppert, 2001)
Argilas
Areias
Razão de pré-adensamento (OCR)
Densidade relativa (DR)
Resistência não drenada (Su)
Ângulo de atrito efetivo (φ’)
Coeficiente de empuxo no repouso (ko)
Coeficiente de empuxo no repouso (ko)
Módulo de Young não drenado (Eu)
Módulo edométrico (M)
Módulo cisalhante máximo (Gmax)
Sensitividade (Sf)
Coeficiente de adensamento (ch ou cv)
Módulo de Young (E)
Módulo edométrico (M)
Módulo cisalhante máximo (Gmax)
.
O procedimento padrão do ensaio de cone consiste na cravação estática da
ponteira cônica (com 60º de ápice) sob velocidade constante de 20mm/s. A seção
26
transversal do cone é normalmente de 10cm², podendo atingir 15cm² para
equipamentos mais robustos. Existem diferentes tipos de equipamentos, que podem
ser classificados em três categorias:
- o cone mecânico, caracterizado pela medida na superfície, com a
transferência mecânica pelas hastes, dos esforços necessários para cravar a ponta
cônica qc e o atrito lateral fs;
- o cone elétrico, cujas células de carga instrumentadas permitem a medida
de qc e fs diretamente na ponteira;
- o piezocone, que além das medidas elétricas de qc e fs, permite o
monitoramento contínuo das poropressões geradas durante o processo de cravação.
A Figura 3 apresenta uma ilustração típica do piezocone. Um aspecto importante do
piezocone é a falta de consenso em relação à localização do elemento filtrante, para
registro das poropressões geradas durante a cravação (Robertson et al, 1992;
Schnaid et al, 2000). A escolha de uma posição particular: ponta (u1), base (u2) ou
luva (u3) dependerá da aplicação dada às poropressões registradas no ensaio.
FIGURA 3 - ILUSTRAÇÃO DO PIEZOCONE
Fonte: (Schnaid, 2000).
O equipamento de cravação consiste de uma estrutura de reação sobre a
qual é montado um sistema de aplicação de cargas. Em geral, são utilizados
sistemas hidráulicos para essa finalidade, sendo o pistão acionado por uma bomba
hidráulica acoplada a um motor de combustão ou elétrico. A penetração é executada
através da cravação contínua de hastes de comprimento de 1.00m, seguida da
27
retração do pistão hidráulico para posicionamento de nova haste. O conjunto pode
ser montado sobre um caminhão, cuja capacidade varia entre 10 e 20 toneladas. A
reação aos esforços de cravação é obtida pelo peso próprio do equipamento. O
principal atrativo do ensaio é o registro contínuo da resistência à penetração,
fornecendo uma descrição detalhada da estratigrafia do subsolo.
Figura 4 - Equipamentos utilizados para a realização do ensaio CPT e CPTU.
Fonte : ( http://www.insitu.com.br )
A Figura 5 apresenta alguns resultados típicos de ensaios de piezocone. No
caso do CPT, as grandezas medidas são: resistência de ponta qc e atrito lateral fs. A
razão de atrito é o primeiro parâmetro derivado do ensaio, utilizado na classificação
dos solos.
*
* : <;
(1)
=
A partir dos resultados de ensaios de piezocone, podem ser estimadas várias
propriedades de solos argilosos e arenosos, conforme descrito a seguir.
28
Figura 5 - Resultados Típicos de um Ensaio de Cone
Fonte : ( http://www.insitu.com.br )
2.2.2.2.
SOLOS ARGILOSOS
Formatado: Nível 4
2.2.2.2.1. RESISTÊNCIA NÃO-DRENADA (Su)
Formatado: Nível 5
A resistência não drenada pode ser estimada a partir das equações propostas
por Lunne Et Al (1997) ( adapatado de Schnaid, 2000 ) :
:
><? @ABC D
: EFG
∆I
E∆I
( 2)
(3)
29
Onde
JK
e
são os fatores de cone em termos de resistência de ponta e
∆
de poropressão, respectivamente. Os valores de
JK
e
∆
podem ser estimados
através de ábacos ou previamente obtidos a partir de correlações entre ensaios de
piezocone e de palheta.
2.2.2.2.2. COEFICIENTE DE ADENSAMENTO HORIZONTAL ( ) DO
SOLO
Ensaios de dissipação do excesso de poropressões geradas durante a
cravação do piezocone no solo podem ser interpretados para a obtenção do
coeficiente de adensamento horizontal ( ). O ensaio consiste em interromper a
cravação do cone em profundidades pré-estabelecidas, por um período de
aproximadamente 1 hora, até atingirem-se 50% de dissipação do excesso de
poropressão.
O método de estimativa de mais utilizado é o proposto por Houlsby e Teh
(1988) que leva em conta o índice de rigidez Ir do solo:
∗
= & ∙ 2 ∙ Q
OP R
(4)
onde:
= raio do piezocone;
= tempo de dissipação;
= índice de rigidez;
T* = fator tempo, obtido a partir da Tabela 4 para as duas posições mais
utilizadas do elemento poroso;
Sendo:
S
= T
I
(5)
Formatado: Nível 5
30
Onde:
G = módulo de cisalhamento do solo.
Tabela 4 - Fator tempo T* para análise dos ensaios de dissipação
Fonte : (Schnaid, 2000 adaptado de Houlsby e Teh, 1988).
∆U
∆UV
Fator tempo T*
(%)
20
Elemento poroso na face
do cone (ut)
1.040
Elemento poroso na base
do cone (ub)
1.600
30
0.463
0.804
40
0.226
0.439
50
0.118
0.245
60
0.063
0.142
70
0.032
0.078
80
0.014
0.038
O conhecimento da magnitude da tensão de pré-adensamento do solo é
fundamental na análise do comportamento de depósitos de argilas moles. A história
de tensões de um depósito, ou seja, a variação da tensão de pré-adensamento
(′$ ) com a profundidade pode ser estimada através das seguintes correlações
propostas por Mayne e Holtz (1988):
′$ = 0,33 ∙ ( − )
(6)
′$ = 0,47 ∙ ( − )
(7)
′$ = 0,54 ∙ ( − )
(8)
onde:
=
tensão vertical in situ;
=
poropressão medida na face do cone;
=
poropressão medida na base do cone;
31
=
poropressão hidrostática.
A razão de pré-adensamento (OCR) de um depósito argiloso pode ser então
determinada através da equação:
^ = 2.2.2.3.
AB_
(9)
ABC
SOLOS ARENOSOS
Formatado: Nível 4
2.2.2.3.1. DENSIDADE RELATIVA
Formatado: Nível 5
Para solos granulares, a medida da resistência de ponta do cone (qT) pode
ser utilizada na previsão da densidade relativa (
). Pesquisas em câmaras de
calibração
foram
determinantes
para
o
desenvolvimento
de
correlações,
gradativamente incorporadas à prática de engenharia (Robertson & Campanella,
1988; Jamiolkowski, et al, 1985) O valor de pode ser determinado através da
equação:
= −98 + 66 log)
<=
(ABg )C,h
(10)
sendo e ′i expressos em t/m².
2.2.2.3.2. ÂNGULO DE ATRITO INTERNO DO SOLO (φ’)
Formatado: Nível 5
A partir do valor da densidade relativa do solo, pode-se obter o ângulo de
atrito através das seguintes correlações:
(1,49 − ) ∙ tan n′ = 0,712
(11)
n = 33 + {3 ∙ p
(10 − !q ) − 1r}
(12)
32
2.2.2.3.3. MÓDULO DE DEFORMABILIDADE (E)
Formatado: Nível 5
Inúmeras correlações entre o módulo de deformabilidade e a resistência à
penetração (qc) têm sido propostas na literatura. No entanto, na ausência de
correlações desenvolvidas e validadas para solos arenosos brasileiros, recomendase a utilização da expressão de Baldi Et Al (1981) para uma primeira estimativa do
módulo E25:
= 1,5 ∙ (13)
onde:
=
módulo de deformabilidade correspondente a 25% da tensão
desviadora máxima.
2.2.3. ENSAIOS DE PALHETA (“VANE TEST”)
O ensaio de palheta (Vane Test) foi desenvolvido na Suécia, em 1919, por
John Olsson. Ao término da década de 1940 foi aperfeiçoado, assumindo a forma
empregada até hoje. Em 1987 a ASTM realizou conferência sobre o tema, que pode
servir de referência internacional. No Brasil o ensaio foi introduzido em 1949 pelo
Instituto de Pesquisas Tecnológicas de São Paulo (IPT). O ensaio de palheta foi
normalizado pela Associação Brasileira de Normas Técnicas (ABNT) em outubro de
1989.
O ensaio de palheta é um método semi-indireto de investigação do subsolo.
Este tipo de ensaio não fornece informações sobre a natureza do terreno, sendo
estas informações obtidas a partir de correlações indiretas.
O principal objetivo dos ensaios “Vane” é a determinação da resistência ao
cisalhamento não-drenada de um estrato argiloso, podendo-se obtê-la tanto para
amostras em estado indeformado, quanto para amostras em estado deformado ou
amolgado. A partir de variações das formas e dimensões da palheta, pode-se ainda
investigar a anisotropia da resistência não-drenada do material.
Formatado: Nível 3
33
A parte essencial do aparelho é uma palheta que consiste em um eixo de aço
no qual estão soldadas quatro aletas finas e retangulares. As palhetas usuais têm
uma altura igual a 130mm e um diâmetro de 65mm (altura igual ao dobro do
diâmetro). No entanto, admite-se também palhetas com diâmetros de 55mm e
88mm. A palheta é ligada a uma haste de aço, capaz de suportar os torques
aplicados. A haste conduz a palheta até a profundidade de realização do ensaio.
O equipamento é composto de uma “mesa” fixada à boca do revestimento,
onde estão os dispositivos para a aplicação de um momento de torção à
extremidade da haste. O equipamento de aplicação e medição do torque, projetado
para imprimir uma rotação ao conjunto de 6º/min, deve possuir um mecanismo de
coroa e pinhão acionado por manivela (Figura 6 e 7).
A medida do momento é feita através de anéis dinamométricos e de vários
tipos de instrumentos com molas, capazes de registrar o momento máximo aplicado.
Alguns instrumentos registram o momento num diagrama onde a máxima leitura é
obtida por calibração do aparelho.
34
Figura 6 - Equipamento para Ensaio de Palheta “in situ”
Fonte: (Ortigão e Collet, 1987).
35
Figura 7 - Equipamento para Ensaio de Palheta
Fonte : ( http://www.insitu.com.br )
A idéia básica do ensaio consiste em cravar no maciço de solo uma palheta
cruciforme, que é submetida ao torque necessário para que ocorra o cisalhamento
do solo por rotação, em condições não drenadas.
Com o valor da força obtido, calcula-se a resistência unitária ao cisalhamento,
desenvolvida pela superfície lateral do cilindro e pelas superfícies circulares
correspondentes ao seu topo e base.
A instalação da palheta até a profundidade do ensaio pode ser feita por
cravação estática, ou no interior de um furo aberto a trado ou, ainda, por circulação
de água.
36
Para a primeira hipótese é necessário que não haja camadas resistentes
sobrejacentes à argila a ensaiar e que a palheta esteja munida de uma sapata de
proteção durante a cravação.
O ensaio propriamente dito é feito girando-se a manivela com uma velocidade
tal que a velocidade transmitida à palheta seja constante e igual a 6º/min. A
deformação da mola ou anel dinamométrico é lida de ½ em ½ minuto (3º em 3º). No
momento em que as leituras atingem um máximo, o ensaio é suspenso.
Para a medição da resistência amolgada da argila, imediatamente após a
aplicação do torque máximo, são realizadas 10 revoluções completas na palheta e o
ensaio é refeito.
A Figura 8 apresenta curvas típicas, rotação da palheta versus momento, de
ensaios em argila sensível natural e amolgada.
A relação entre o momento máximo da curva natural e o correspondente à
curva amolgada define a sensibilidade da argila.
Figura 8 - Curvas típicas torque x ângulo de rotação em ensaios de palheta.
Fonte : (Schnaid, 2000).
Com base no torque medido, é possível determinar a resistência ao
cisalhamento não drenada do solo ( ), conforme a expressão:
= ,tuv
wxy
(14)
37
onde:
M
=
torque máximo medido;
D
=
diâmetro da palheta
O valor da resistência não drenada amolgada ( ) é obtido pela mesma
equação apresentada anteriormente, porém, com o valor do torque correspondente
à condição amolgada.
Com os valores de e determina-se o valor da sensibilidade da argila
(St):
= TI
(15)
TIP
A Tabela 5 apresenta a classificação das argilas, de acordo com a
sensibilidade.
Tabela 5 - Sensibilidade das argilas
Fonte : ( Skempton e Northey, 1952)
Sensibilidade
St
Baixa
2–4
Média
4–8
Alta
8 –16
Muito alta
> 16
O ensaio de Palheta é tradicionalmente utilizado para a determinação da
resistência não drenada e da sensibilidade de depósitos de argilas moles.
2.3.
ENSAIOS DE LABORATORIO
2.3.1. GENERALIDADES
No laboratório, além das características físicas do material, pode-se também
determinar suas propriedades de mecânica tais como resistência, permeabilidade e
compressibilidade. Para a realização desses ensaios são necessárias amostras de
solos. Alguns ensaios requerem amostras que guardam todas as características do
Formatado: Nível 2
Formatado: Nível 3
38
solo no campo, ou seja, amostras indeformadas. Este tipo de amostra requer
técnicas de amostragem mais sofisticadas. No entanto, a maioria dos ensaios
utilizados para a determinação das características físicas do material é realizada
com amostras deformadas.
Os ensaios de laboratório têm grande importância para determinação dos
parâmetros de deformabilidade e resistência dos solos. Estes parâmetros não são
características físicas do material, e dependem de fatores como tipo de
carregamento, condições de drenagem, trajetória de tensão e tempo de
carregamento.
2.3.2. ENSAIOS DE COMPACTAÇÃO DE PROCTOR
Nem todos os terrenos naturais em, que se propõe realizar algum tipo de
fundação, são adequados. Um terreno granular solto, por exemplo, pode sofrer
deformações elásticas inadmissíveis. O mesmo pode ocorre a um terreno coesivo
por motivos de consolidação. Tem se então que realizar uma melhora nesse solo.
O processo de compactação consiste na densificação de um solo por meio de
um equipamento mecânico. O objetivo da compactação é reduzir o índice de vazios
do solo. O aumento da densidade, ou redução do índice de vazios, ocasiona uma
melhoria nas propriedades dos solos. Na compactação, as quantidades de partículas
sólidas e de água permanecem constantes e o aumento da massa específica
corresponde à eliminação de ar dos vazios.
Em 1933, Proctor divulgou suas observações sobre a compactação dos solos,
mostrando que, para uma dada energia de compactação, o peso específico seco ( )
é função do teor de umidade do solo. Para baixos valores de umidade, a saída da
água é facilitada, pois o ar se encontra em forma de canalículos intercomunicados. A
partir de certo teor de umidade, a compactação não é capaz de expulsar o ar dos
vazios, pois o grau de saturação é elevado e o ar está ocluso. Há, portanto, um
determinado valor de umidade, denominado umidade ótima, que conduz a uma
densidade máxima.
Para a execução do ensaio de compactação Proctor, a amostra deve ser
previamente seca ao ar e destorroada. Inicialmente, acrescenta-se água até que o
solo fique com uma umidade cerca de 5% abaixo da umidade ótima. Uma vez
uniformizada a umidade da amostra, uma porção de solo é colocada em um cilindro
Formatado: Nível 3
39
padrão com 10 cm de diâmetro e 12.73cm de altura. A amostra é então submetida a
26 golpes de um soquete com massa de 2.5kg, caindo de uma altura de 30.5cm. A
porção do solo compactado deve atingir 1/3 da altura do cilindro. O processo é
repetido mais duas vezes, atingindo-se a altura total do cilindro. Neste momento,
determina-se a massa específica e o teor de umidade do corpo de prova. Com estes
valores, calcula-se a densidade seca.
Figura 9 – Cilindro padrão para Realização do Ensaio de Proctor
Fonte: ( http:// www.insitu.com.br )
Com os valores, do peso específico do solo e teor de umidade, pode-se
calcular o peso específico aparente seco mediante a fórmula de correlação:
z
z{ = (|}~)
(16)
Junto com a curva de compactação, sempre que necessário, pode-se
desenhar as curvas representativas de um mesmo grau de saturação, a partir da
equação:
40
'
€; .‚.€ƒ
;.€ƒ„€ .ƒ
…
(17)
onde:
γ= peso específico aparente seco;
γ = peso específico real dos grãos;
γ = peso específico da água;
S = grau de saturação;
w = teor de umidade.
Com o desenvolvimento da engenharia mecânica, foram lançados no
mercado equipamentos de compactação capazes de fornecer maior energia de uma
forma econômica, gerando a necessidade de se normalizar ensaios com diferentes
energias (intermediária e modificada), conforme mostrado na Tabela 6 . A energia de
compactação por unidade de volume pode ser calculada, através da fórmula:
=
†..E.(
‡
= energia de compactação por unidade de volume;
= peso do soquete;
ℎ = altura de queda do soquete;
= número de golpes por camada;
! = número de camadas;
" = volume do solo compactado.
(18)
41
Tabela 6 - Energias de compactação
Fonte : ( Santos, 2008 )
Ensaio de Compactação
P(kg) h(cm)
N
n
V(cm³) E(kg.cm/cm²)
Normal
2.5
30.5
3
26
1000
5.7
Intermediário
4.5
45.7
5
26
2085
12.6
Modificado
4.5
45.7
5
55
2085
26.6
Terminado o ensaio, a amostra é destorroada, a umidade aumentada, o
processo é repetido e obtém-se um novo par de valores umidade-densidade seca. O
ensaio é repetido até que se perceba que a densidade seca, após atingir um valor
máximo, começa a decrescer.
A curva de compactação é obtida pela representação da densidade seca em
função do teor de umidade, como indica a Figura 10. O ponto máximo da curva
define uma densidade seca máxima, à qual corresponde uma umidade ótima.
Figura 10 - Curva obtida em ensaio de compactação Proctor Normal.
Fonte : ( Santos, 2008 )
Um mesmo solo, quando compactado com energias diferentes, apresentará
valores de peso específico aparente seco máximo maiores e teor de umidades
42
ótimas menores, para valores crescentes dessa energia, o ponto se deslocará para
cima e para a esquerda, conforme mostra a Figura 11.
Figura 11 - Curvas de compactação de um solo com diferentes energias.
Fonte : ( Santos, 2008 )
Segundo VARGAS, 1997, a natureza do solo, influência nos valores do peso
específico aparente seco máximo e do teor de umidade ótima. Ao se tentar
compactar um solo, o esforço de compactação será mais ou menos efetivo conforme
a granulometria e plasticidade. As curvas da Figura 12 ilustram este fato mostrando
curvas de compactação obtidas, em amostras de vários solos brasileiros, no ensaio
normal de compactação.
Em geral, para o mesmo esforço de compactação (E) atinge-se nos solos
arenosos (ou materiais granulares bem graduados) maiores valores de peso
43
específico aparente seco máximo sob menores teores de umidade ótima, do que
solos argilosos finos (uniformes).
A secagem de um solo argiloso, dependendo do argilo-mineral que o compõe,
poderá alterar de forma irreversível as suas características, refletindo nos valores
das coordenadas do ponto de máximo da curva de compactação. Assim como a
secagem, também a forma de realizar o ensaio, utilizando uma única amostra de
solo (com reuso) para todos os pontos ou uma amostra nova (sem reuso) para cada
ponto, apresentará valores diferentes para as coordenadas do pico da curva. Por
isso, se recomenda que os solos argilosos não sejam secos diretamente ao sol ou
em estufa e que o ensaio seja realizado com amostras secadas à sombra, sempre
que necessário.
Figura 12 - Curvas de compactação normal de alguns solos brasileiros.
Fonte : ( Maccaferri )
44
2.3.3. ENSAIO DE COMPRESSÃO EDOMÉTRICA
2.3.3.1.
Formatado: Nível 3
GENERALIDADES
Formatado: Nível 4
É de conhecimento geral que qualquer material sujeito a uma determinada
solicitação se deforma no sentido de suportar essa solicitação. Isto é, nenhum
material pode suportar uma solicitação sem se deformar, sendo o valor dessa
deformação dependente do tipo de solicitação e do tipo de material em questão.
Ao solicitar um solo confinado ele se deforma no sentido de absorver essa
solicitação. Do fato de que o solo se encontrar confinado, ocorrem apenas
extensões verticais. Do exposto conclui-se que num estrato confinado só existe
deformação se ocorrer variação de volume.
Dentre os parâmetros de compressibilidade que o engenheiro geotécnico
necessita para a execução de projetos e o estudo do comportamento dos solos,
destacam-se a pressão de pré-adensamento (′$ ), o índice de compressão ( ) e
o coeficiente de adensamento ( ).
Atualmente, a obtenção desses parâmetros se dá a partir de resultados de
ensaios de compressibilidade do solo, sendo, atualmente, várias modalidades de
ensaios de compressão. Esses ensaios de compressão podem ser agrupados
segundo a forma de aplicação das tensões ou deformações em dois grupos:
- Ensaio a carregamento incremental.
- Ensaio a carregamento contínuo.
2.3.3.2.
ENSAIO
DE
COMPRESSÃO
COM
CARREGAMENTO
INCREMENTAL
Este ensaio de compressão edométrica, comumente denominado “ensaio de
adensamento convencional”, é o tipo mais antigo e mais conhecido para
determinação dos parâmetros de compressibilidade dos solos. O ensaio consiste na
compressão axial de um corpo de prova, confinado lateralmente, pela aplicação de
pressões verticais, com duração e razão de carregamento pré-definidas, comumente
com duração de 24 horas e razão de carregamento igual a 1.
Formatado: Nível 4
45
Figura 13 - Prensa de compressão Edométrica.
Fonte : ( Santos, 2008 )
O equipamento utilizado nesse ensaio está apresentado na Figura 13. Além
da prensa apresentada na Figura 13, são ainda necessários para a realização de um
adensamento edométrico incremental, os itens listados abaixo:
1. Célula rígida para confinamento da amostra.
2. Anel de moldagem, biselado.
3. Placa de topo ou placa de carregamento.
4. Pedras porosas.
5. Medidor de deslocamento.
6. Pesos.
7. Cronômetro.
8. Papel filtro.
9. Balança com sensibilidade de 0.01 g.
10. Cápsulas de alumínio.
46
11. Ferramentas de moldagem.
Figura 14 - Esquema da câmara de ensaio de compressão Edométrica.
Fonte : ( Santos, 2008 ).
O ensaio edométrico é realizado uma amostra cilíndrica, com dimensões, em
geral, de 19 mm de espessura e 70 mm de diâmetro é solicitada de acordo com as
hipóteses base da Teoria de Consolidação Unidimensional de Terzaghi:
- o solo encontra-se saturado (submerso);
- o solo encontra-se confinado, sendo as deformações verticais (anel rígido);
- o fluxo é vertical (anel impermeável).
Após a recolha, preparação e corte da amostra, ela é colocada no edómetro e
submetida a carregamentos progressivos (por meio de um sistema de pesos e
alavancas), respeitando em geral as seguintes condições:
- cada carregamento (escalão de carga) é mantido por um período de 24h. O
primeiro estádio de carregamento foi de 13kPa, com 6 estádios de carregamento
que foram aplicados à amostra, ou seja, a variação de carregamento foi de 13kPa,
25kPa, 50kPa, 100kPa, 200kPa e 400kPa;
- durante a fase de carga, cada carregamento adicional (novo escalão de
carga) duplica o que se encontrava aplicado anteriormente;
- em geral é realizada, pelo menos, uma fase de descarga, na qual, em cada
escalão, a carga se vai progressivamente reduzindo para ¼ da anterior (menores
47
deformações na descarga);
- o ensaio deve abranger um campo de tensões relevante para o problema
em estudo tal que permita definir com rigor os parâmetros de compressibilidade mais
importantes do solo.
Durante a realização de cada estágio de carregamento são feitas medidas de
compressão vertical da amostra em função do tempo, para os tempos de 0, 0.15,
0.29, 1, 2, 4, 9, 16, 25, 36, 49, 64, 120, 240, 480, 1440 minutos. Com estes dados
constroem-se as curvas de recalque, ou seja, compressão versus o tempo. Com o
auxílio dessas curvas, determina-se o coeficiente de adensamento do solo por um
dos processos encontrados na literatura tais como: o método de Casagrande (escala
de log t) ou o método de Taylor (escala t), como será descrito mais adiante. A Figura
14 apresenta uma curva típica de recalque.
Com o desenvolvimento do processo de adensamento, ocorre a dissipação
das poropressões na amostra. Considerando-se que o grau de adensamento da
amostra para um determinado fator tempo & é idêntico à porcentagem média de
dissipação da poro-pressão, no final do processo de adensamento (U = 100%) o
acréscimo da tensão efetiva vertical ao longo de toda a espessura da amostra será
igual ao acréscimo de tensão total aplicada no topo da amostra.
Com os valores de deformação, ao final de cada estádio de carregamento,
constrói-se uma curva da tensão efetiva versus a deformação produzida pelo
acréscimo desta tensão, como ilustrado pela Figura 15. Esta curva pode ser
apresentada de várias formas, tais como tensão efetiva vertical versus índice de
vazios, tensão efetiva vertical versus deformação volumétrica específica, dentre
outras formas.
48
Figura 15 - Curva de compressão edométrica de uma argila mole.
Fonte : (Santos, 2008).
Através da curva de compressão edométrica pode-se determinar a Tensão de
pré adensamento (′$ ). Existem na literatura vários métodos para a determinação
da tensão de pré-adensamento, entre eles se pode destacar:
- Método de Casagrande
- Método de Pacheco Silva
2.3.3.3.
MÉTODO DE CASAGRANDE
A determinação da tensão de pré-adensamento pelo método de Casagrande
apresentado por Taylor, 1948, pode ser feita através da curva índice de vazios
versus a tensão efetiva vertical, na escala logarítmica, ou seja, a curva e versus log
′ . Sobre essa curva, estima-se o ponto de maior curvatura (ponto A na Figura 16)
e através deste ponto, traça-se uma horizontal (H) e uma tangente (T) à curva.
Marca-se em seguida a bissetriz (B) do ângulo formado entre a horizontal (H) e a
tangente (T). A abscissa do ponto de interseção da bissetriz com o prolongamento
da reta virgem representa a tensão de pré-adensamento, ′$ .
Formatado: Nível 4
49
Figura 16 - Construção gráfica para a determinação da tensão de pré-adensamento.
Fonte : ( Barros, 1997 )
2.3.3.4.
MÉTODO DE PACHECO SILVA
Formatado: Nível 4
Para se determinar a tensão de pré-adensamento pelo método de Pacheco
Silva (1970), o seguinte procedimento é seguido: Na curva índice de vazios versus a
tensão efetiva vertical, e versus log ′ traça-se uma reta horizontal passando pelo
índice de vazios inicial, % .
Prolonga-se a reta virgem até interceptar a horizontal por % , ponto A na
Figura 17. Pelo ponto A é traçada uma vertical até interceptar a curva de
compressão no ponto B, e por esta interseção traça-se uma horizontal. A abscissa
da interseção dessa horizontal com o prolongamento da reta virgem, ponto C na
Figura 17, representa a tensão de pré-adensamento, ′$ ,
método de Pacheco Silva.
determinada pelo
50
Figura 17 - Construção gráfica para a determinação da tensão de pré-adensamento.
Fonte: (Pacheco Silva, 1970).
2.3.3.5.
DETERMINAÇÃO DO COEFICIENTE DE ADENSAMENTO
O coeficiente de adensamento de uma camada argilosa, ˆ , determina a
velocidade na qual um solo se deforma quando solicitado por acréscimo de tensão,
∆. Pode-se dizer que para um mesmo solo, quanto maior a permeabilidade do solo,
mais rápido se dará o adensamento, pois ˆ será maior. Por outro lado, quanto mais
compressível for o solo, tanto maior será o tempo necessário para que o
adensamento se processe totalmente, uma vez que maior quantidade de água terá
que sair da massa de solo, e assim o solo apresentará menor ˆ .
Com os dados obtidos de um ensaio de adensamento edométrico, o
coeficiente de adensamento do solo pode ser obtido através dos Métodos de Taylor
ou de Casagrande.
Os métodos de Taylor e de Casagrande são os mais conhecidos e
comumente empregados para a determinação do coeficiente de adensamento.
Formatado: Nível 4
51
O método de Casagrande é de difícil de utilizar no caso de solos com
elevados coeficientes de consolidação e/ou sofrendo assentamentos em que a
fluência constitui uma componente importante.
O método de Taylor, porque se baseia na interpretação da fase inicial da
consolidação, é menos influenciado pela ocorrência de fluência durante o ensaio,
contudo exige maior número e precisão de leituras no início do processo (requisito
facilmente satisfeito por meio da aquisição automática de dados).
A solução da equação diferencial de adensamento de Terzaghi fornece uma
função u(z,t), que é a função de distribuição do excesso de poro pressão ao logo da
espessura camada de solo para um tempo t qualquer.
O valor do grau médio de adensamento, U, pode ser expresso com excelente
aproximação pelas seguintes equações empíricas:
- Quando U ≤ 60%:
w
& = ‰ Š
(19)
- Quando U > 60%:
& = −0,9332 ∙ log(1 − Š) − 0,0851
(20)
Nestes dois métodos a determinação de ˆ é feita utilizando-se de ajustes da
curva de formação versus tempo obtida do ensaio de adensamento oedométrico
incremental.
Ambos os métodos utilizam propriedades características e distintas da curva
teórica de adensamento de Terzaghi, ou seja, da semelhança da curva real de
deformação versus tempo (em suas respectivas escaladas de tempo) com a curva
teórica U versus & .
52
2.3.3.6.
MÉTODO DE TAYLOR
Formatado: Nível 4
Segundo o método de Taylor, os dados de deformação devem ser traçados
em uma escala aritmética versus a raiz quadrada do tempo, sendo desta forma
também chamado de “Método da raiz de t”. O método de Taylor consiste em se
determinar o início, do, do adensamento, através de um ajuste fase linear da curva
de adensamento. O início do adensamento é determinado pela interseção da fase
linear, extrapolada, com o eixo das deformações, como mostrado na Figura 18. Uma
segunda reta com abscissa 1.15 vezes maior do que a reta da fase linear e traçada,
pr = 1.15 pq. Essa segunda reta intercepta a curva de compressão de laboratório no
ponto A, onde U = 90 %. A abscissa do ponto A é 90 t . Com o valor de ‹ e &‹ =
0.848 (fator tempo para U= 90 %) o coeficiente de adensamento do solo pode ser
determinado como:
ˆ = 0,848 ∙
Œ… R
C
(21)
O valor de 9' a ser utilizado na equação (21) é a máxima distância de
drenagem a 50 % de deformação, ou seja, é a média de 9' para o início e o fim do
estádio de carregamento.
53
Figura 18 - Curva de recalque na escala da raiz do tempo para a determinação de cv
Fonte : ( Santos, 2008 ).
Para a utilização do método de Casagrande para a determinação do
coeficiente de adensamento é necessário que os resultados de deformação sejam
traçados em uma escala aritmética, sendo o tempo representado na escala
logarítmica, por este motivo, este método é também chamado de “Método log t”.
Casagrande, em seu método, corrige a deformação elástica inicial
determinando-se o foco da parábola que representa 0% do adensamento primário. A
determinação do foco desta parábola no gráfico da deformação versus log t, ou seja,
inicio do adensamento, é feita tomando-se dois tempos, t1 e t2, tal que t2 = 4t1. Em
seguida, a diferença de deformação entre t1 e t2, distância vertical entre P e Q, é
subtraída do valor da deformação correspondente ao tempo t1, ponto P, como
mostrado na Figura 19. O final do adensamento primário é determinado através da
interseção da fase linear da curva de recalque com o prolongamento da fase de
compressão secundária, ponto T na Figura 19.
Com a média dos valores de 0% e 100% de adensamento calcula-se a
deformação para 50% do adensamento e determinar a partir da curva de
adensamento o tempo , que representa o tempo necessário para transcorrer 50 %
do adensamento, conforme indicado na Figura 19. Com os valores de , & =
54
0.197 e 9' correspondente a 50% de deformação se calcula, então, ˆ pela
equação.
ˆ = 0,197 ∙
Œ… R
hC
(22)
Figura 19 - Curva de recalque, método do logaritmo do tempo
Fonte : (Casagrande, 1937, p.).
2.3.4. ENSAIO DE CISALHAMENTO DIRETO
O ensaio de cisalhamento direto é utilizado para a determinação dos
parâmetros de resistência ao cisalhamento dos solos. Este ensaio permite o estudo
da resistência em um plano de ruptura, pré-fixado.
Neste ensaio a amostra de solo é colocada em uma caixa dividida em 2
metades, como esquematizado na Figura 20. Inicialmente, aplica-se sobre a amostra
uma força vertical N. Em seguida, uma força tangencial T é aplicada à metade
superior da caixa, de modo a provocar o deslocamento de uma metade da caixa em
relação à outra, até a ruptura. As tensões normal (σ) e tangencial (τ) no plano de
ruptura podem ser calculadas a partir das expressões:
Formatado: Nível 3
55
E
= (23)
Ž
 = K
Ž
(24)
onde:
 é a área da seção transversal da amostra.
A tensão cisalhante & pode ser representada em função do deslocamento no
sentido do cisalhamento, como indica a Figura 21. O deslocamento vertical também
é registrado durante o ensaio, indicando se houve diminuição ou aumento de volume
durante o cisalhamento.
Os parâmetros de resistência dos solos são determinados diretamente da
envoltória de resistência, como mostra a Figura 22. A envoltória de resistência pode
ser obtida a partir de resultados de ensaios de cisalhamento direto executados sob
diferentes valores de tensão normal.
Figura 20 - Esquema do equipamento de cisalhamento direto.
Fonte : ( Maccaferri ).
56
Figura 21 - Resultado típico de um ensaio de cisalhamento direto.
Fonte : ( Pinto, 2000 ).
57
Figura 22 - Envoltória de resistência.
Fonte : ( Santos, 2008 ).
2.3.5. ENSAIO DE COMPRESSÃO TRIAXIAL
O ensaio triaxial é utilizado para a determinação dos parâmetros de
deformabilidade e resistência dos solos.
Este ensaio é realizado utilizando-se corpos de provas cilíndricos moldados a
partir de amostras indeformadas e consiste na aplicação de um carregamento axial
sobre um corpo de prova cilíndrico de solo, submetido a um estado hidrostático de
tensões.
O corpo de prova é colocado dentro de uma câmara de ensaio (Figura 23),
envolvido por uma membrana de borracha. Em contato direto com o corpo de prova
utiliza-se uma tira de papel filtro em espiral, cujo objetivo é diminuir o caminho de
drenagem ao longo da amostra. Pedras porosas são instaladas no topo e na base
do corpo de prova para facilitar a drenagem.
A câmara é preenchida com água, à qual se aplica uma pressão, que é
chamada pressão confinante do ensaio. A pressão confinante atua em todas as
direções, submetendo o corpo de prova a um carregamento hidrostático.
Formatado: Nível 3
58
Figura 23 - Aparelho de compressão triaxial
Fonte : ( Souza Pinto, 2000).
A carga axial é aplicada através de um pistão que penetra na câmara e é
medida por meio de um anel dinamométrico externo, ou por uma célula de carga
intercalada no pistão. Durante os carregamentos, mede se em intervalos de tempo,
o acréscimo de tensão axial que está atuando e a deformação vertical do corpo de
prova. Esta deformação dividida pela altura inicial da amostra fornece a deformação
vertical específica. A ruptura é obtida com σ1, e os círculos de Mohr são traçados
com os pares (σ1, σ3) obtidos no ensaio e em seguida a envoltória de Coulomb,
conforme mostrado na figura 24.
59
Figura 24 - Aplicação da tensão principal σ1 e da tensão de confinamento σ3; (b)
corpo de prova rompido; (c) Circulos de Mohr e envoltória de Coulomb.
Fonte : (Barros, 1995).
A força normal que é aplicada ao corpo de prova pelo pistão axial, dividida
pela seção transversal do corpo de prova e somada a σ3 corresponde à pressão
axial σ1. A pressão neutra desenvolvida na água intersticial do corpo de prova é
medida utilizando-se um aparelho capaz de medir pressões na água sem exigir
variações de volume d’água intersticial da amostra.
Existem três maneiras de se realizar o ensaio triaxial:
a) ensaio não adensado e não drenado (UU – unconsolidated undrained) ou
ensaio rápido ( Q de quick): Este ensaio é recomendado quando se deseja obter a
coesão e ângulo de atrito de por exemplo um talude, logo após a sua execução.
Neste ensaio o corpo de prova é submetido à pressão confinante (σ3) e depois ao
carregamento axial, sem se permitir a drenagem da água intersticial (sem conectar
as buretas). O teor de umidade permanece constante e no caso da amostra estar
saturada, não ocorre variação de volume. Quando colocada uma barra sobre a letra
Q significa que o ensaio é feito com medidas de pressões neutras. O ensaio Q será
o mesmo só que sem a medida dessas pressões. Este ensaio demora cerca de 1 a
2 horas.
b) ensaio adensado não drenado (CU – consolidated undrained) ou ensaio
rápido pré-adensado (R): este ensaio é o que melhor representa as condições do
solo para a análise da estabilidade de um aterro certo tempo após a sua construção,
ou da estabilidade de uma barragem em virtude de um rebaixamento rápido do
reservatório. Neste ensaio é aplicada a pressão confinante (σ3) e deixa-se dissipar a
pressão neutra correspondente, adensando o corpo de prova com σ3 (conecta-se as
buretas para o pré-adensamento – cerca de um dia para adensar). Na seqüência
60
aplica-se o carregamento axial σ1, espera estabilizar e rompe sem drenagem. Este
ensaio fornece a resistência não drenada em função da tensão de adensamento. Se
as pressões neutras forem medidas, ter-se-á a resistência em termos de tensões
efetivas, sendo por essa razão bastante empregado por permitir determinar a
envoltória de resistência em termos de tensão efetiva em cerca de dois dias;
c) ensaio adensado drenado (CD – consolidated drained), também chamado
impropriamente de ensaio lento (S - slow), devido à condição de ser um ensaio
muito lento, levando no caso das argila, cerca de duas semanas: Neste ensaio é
permitida em todas as fase, a drenagem do corpo de prova, sendo que muitas vezes
este chega ao laboratório já pré-adensado. É aplicada a tensão confinante (σ3) e
espera-se que a amostra adense, ou seja, que a pressão neutra (u) se dissipe.
Aumenta-se, então, a tensão axial, de maneira a expulsar a água sob pressão,
ocorrendo a dissipação total das pressões neutras durante todo o ensaio, ou seja,
mantendo-se nulas durante todo o ensaio, de maneira que as pressões totais
medidas sejam iguais às efetivas.
61
3.
GEOSSINTÉTICOS
Formatado: Nível 1
3.1.
Formatado: Nível 2
GENERALIDADES
A utilização de materiais como elemento de reforço de solos é prática comum
desde 3000 a.C., onde os babilônios já inseriam materiais fibrosos na construção de
habitações. A muralha da China, construída há dois mil anos, possui seções de
argila e cascalho reforçados com fibras naturais. Os antigos romanos utilizavam
troncos imersos em tipos distintos de solo para a construção de muros de
contenção. Diversos materiais vegetais, constituídos de fibras resistentes, foram
utilizados em obras do Império Romano. Dentre estes materiais, pode-se citar:
estivas de junco, bambu, troncos de árvores, palha, etc.
Porém, com a necessidade de maior resistência e durabilidade dos reforços, a
partir dos anos 50 com o desenvolvimento dos geotêxteis tecidos, deu-se inicio das
inclusões sintéticas afim da melhoria da qualidade do solo.
Pela definição temos:
GEO - Prefixo grego relacionado que significa solo.
SINTÉTICO - Material obtido através de síntese química ou algum
procedimento industrial.
GEOSSINTÉTICO - materiais obtidos através de síntese química ou algum
procedimento industrial que tem como objetivo melhorar o comportamento dos solos.
Numa obra de Engenharia os geossintéticos podem exercer varias funções,
onde segundo VERTEMATTI (2004), são:
- Controle de Erosão Superficial, Prevenção de erosão superficial de
particulas de solo devido a escoamento superficial de um fluido.
- Drenagem, Coleta e condução de um fluido pelo corpo de um geossintético.
- Filtração, Retenção de um solo ou de outras partículas, permitindo a
passagem livre do fluido em movimento.
- Impermeabilização, Bloqueio ou desvio de fluidos.
- Proteção, Limitação ou prevenção de danos a elementos de obras
geotécnicas.
- Reforço, Utilização das propriedades mecânicas de um geossintético para a
melhoria do comportamento mecânico de uma estrutura geotécnica.
62
- Separação, Ação de impedir a mistura ou interação de materiais adjacentes.
A tabela 7 apresenta as principais aplicações dos geossintéticos em função
dos diferentes tipos.
Tabela 7 - Tipos de Geossintéticos e suas principais aplicações
Fonte: ( Vertematti, 2004)
APLICAÇÃO
GEOSSINTÉTICO
(1)
(2)
(3)
(4)
(5)
(6)
(7)
Geotêxtil
x
x
x
x
x
-
x
Geogrelha
x
-
-
-
-
x
-
Geomembrana
x
-
-
-
-
-
x
Georrede
-
x
-
x
-
-
-
-
-
-
-
-
-
x
Geocélula
-
x
-
-
x
x
-
Geotubo
-
-
-
x
-
-
-
Geofibras
-
-
-
-
-
x
-
Geocomposto
Argilioso
3.2.
GEOGRELHA
Segundo Vertematti (2004), as geogrelhas são produtos em forma de grelha
com função predominante de reforço, cujas aberturas permitem a interação do meio
em que estão confinadas, e constituído por elementos resistentes a tração. É
considerado unidirecional quando apresenta elevada resistência à tração apenas em
uma direção, e bidirecional quando apresenta elevada resistência a tração nas duas
direções principais (ortogonais). Em função do processo de fabricação, as
geogrelhas podem ser etrudadas, soldadas ou tecidas.
Formatado: Nível 2
63
Figura 25 - Elementos componentes de uma geogrelha.
Fonte : (TEIXEIRA, 2003)
As principais aplicações das geogrelhas são as seguintes:
• reforço em taludes e muros de contenção;
• separação / reforço em rodovias não pavimentadas e ferrovias;
• em conjunto com outros elementos para construção de muros reforçados
com controle de erosão e encontros de ponte;
• reforço para execução de aterros sobre solos moles;
• reforço de pavimento asfáltico;
• em conjunto com geotêxteis ou geomembranas (formando geocompostos).
Existe uma tendência mundial em se padronizar uma terminologia para se
classificar os geossintéticos, e por conseqüência as geogrelhas. A terminologia
apresentada a seguir e sua respectiva definição leva em conta as recentes
recomendações feitas pela IGS e aquelas especificadas na NBR 12553.
GG - Geogrelhas (geogrid - genérica): estrutura sintética, fabricada em
forma de manta consistindo de uma rede de elementos integralmente conectados
que podem ser unidos por extrusão, colagem ou entrelaçamento. Suas aberturas
são maiores que seus elementos constituintes e são empregadas em aplicações de
engenharia geotécnica, ambiental, hidráulica e viária.
GGE
-
Geogrelha
Extrudada
(extruded
geogrid):
produzida
estiramento uniaxial ou biaxial de uma estrutura extrudada integralmente.
pelo
64
GGB - Geogrelha Ligada (bounded geogrid): produzida através da união,
usualmente em ângulos retos, de dois ou mais conjuntos de fios ou outros
elementos.
GGW - Geogrelha Tecida (woven geogrid): produzida pela tecelagem,
geralmente em ângulos retos, de dois ou mais conjuntos de fibras, fios, filamentos
ou outros elementos.
Os polímeros geralmente empregados na produção de geogrelhas são o
polietileno de alta densidade (PEAD), o poliéster (PET) e o polipropileno (PP). A
Figura 26 mostra as estruturas dos monômeros que dão origem a estes polímeros.
Nestas Figuras, n é denominado “grau de polimerização” e indica o número de vezes
que o monômero se repete no polímero. O peso molecular do polímero, que
influencia sobremaneira o seu comportamento, corresponde ao produto do peso
molecular do monômero pelo grau de polimerização.
Figura 26 - Monômeros dos principais polímeros dos geossintéticos.
Fonte : (Teixeira, 2003)
Outro aspecto importante dos polímeros relaciona-se ao seu grau de
cristalinidade. As porções em que as macromoléculas dos polímeros se alinham em
pequenas regiões são denominadas cristalinas enquanto as não alinhadas
denominam-se amorfas. Os polímeros utilizados em geogrelhas possuem sempre
parte de sua estrutura amorfa e parte cristalina e, por isso, são denominados de
semi-cristalinos.
O tipo de polímero afeta as diversas características de comportamento dos
geossintéticos, principalmente aquelas de longo prazo. Dentre as propriedades
influenciadas pelo tipo de polímero destacam-se a resistência à degradação
química, por ação dos raios ultravioleta, resistência à temperatura, à hidrólise, bem
como os comportamentos mecânicos. A tabela 8 apresenta um resumo do
comportamento de longo prazo dos materiais em função do polímero utilizado.
65
Tabela 8 - Propriedades de degradação dos principais polímeros que constituem as
geogrelhas
Fonte : (adaptado de Jonh, 1987 e den Hoedt, 1988, apud TEIXEIRA, 2003).
POLÍMERO
PROPRIEDADE
PET
PP
PEAD
Foto-degradação
3
3* a 1** 3* a 1**
Termo-oxidação
3
1
1
Hidrólise
1
2
2
Degradação Biológica
3
3
3
Degradação química a álcalis
1
2a3
3
Degradação química a ácidos
2
3
3
Fluência
3
2
2
* com tratamento (por exemplo, negro de fumo); ** sem tratamento
Legenda: resistência elevada (3); média (2) e baixa (1).
Outra propriedade importante devido ao tipo de polímero é a resistência a
tração. A Figura 27 apresenta faixas típicas para a curva tensão/deformação dos
diferentes polímeros em ensaios de tração simples.
66
Figura 27 - Comportamento Tensão vs Deformação de Diferentes Polímeros.
Fonte: ( Manual Maccaferri Simplificado para aplicação de Geossintéticos,
2009 )
Nas primeiras aplicações das grelhas como elementos de reforço de solo,
foram empregas as grelhas metálicas que eram susceptíveis à corrosão. Essa
limitação motivou a indústria ao desenvolvimento de grelhas a partir de materiais
poliméricos que, sendo relativamente inertes, podem ser usados em ambientes
agressivos. Alem disso, as geogrelhas poliméricas também oferecem uma boa
interação com o solo, que é resultante de um efeito conjugado de, atrito entre solo e
superfície da geogrelha e resistência passiva oferecida pelo solo aos seus
elementos transversais.
As propriedades mecânicas de interação entre solo e geogrelha são fatores
importantes para o projeto de estruturas em solo reforçado. Mediante a crescente
necessidade da utilização de geossinteticos em obras de solo reforçado, tem se
desenvolvido ensaios para avaliar a interação solo geogrelha, onde entre estes
temos:
a-) Ensaio de Cisalhamento direto e de Arrancamento: Os ensaios de
arrancamento e de cisalhamento direto diferem entre si basicamente pela forma com
67
que os esforços são aplicados ao geossintético, pelos mecanismos de ruptura
impostos e pelas condições de contorno de cada um, porém ambos tem como
principal objetivo simular o atrito entre o solo e o reforço, onde, o Ensaio de
arrancamento simula o comportamento de geogrelhas ao serem solicitadas em um
maciço reforçado, e o ensaio de cisalhamento direto, simula a situação em que
ocorram um deslizamento relativo de uma camada de solo sobre a geogrelha em
relação a uma camada de solo abaixo dela.
Figura 28 - Esquema ilustrativo dos ensaios de cisalhamento direto e de
arrancamento
Fonte: (Teixeira, 2003).
b-) APSR (Automated Plane Strain Reinforcement cell) : Este equipamento,
foi esenvolvido no MIT por Larson (1992) e permite que os esforços e as
deformações que se desenvolvem no reforço sejam monitorados à medida que a
massa de solo é cisalhada sob condições de deformação plana (σ‘‘ =σ1, σ’’ =σ3 e
ε”” =0), permitindo assim estudada a interação entre solo e reforço sob condições
similares às que ocorrem em estruturas de contenção, onde se desenvolve um
mecanismo de cisalhamento na massa de solo sob condições de deformações
planas, e fornece resultados bastante interessantes.
68
Figura 29 - Diagrama esquemático do equipamento APSR
(Abramento apud Teixeira,2003).
c-) Ensaio de Cisalhamento direto com o reforço inclinado: Este tipo de ensaio
é bastante semelhante ao ensaio de cisalhamento direto convencional, utilizado para
se determinar os parâmetros de resistência na interface solo–geogrelha. A principal
diferença está na posição em que a geogrelha é instalada. Neste ensaio, a amostra
de reforço fica inclinada com relação à caixa de ensaios de tal forma que a
superfície de cisalhamento passe pelo geossintético, conforme mostra a Figura 29. A
geogrelha, por sua vez, deve possuir um comprimento L mínimo para mobilizar
resistência ao arrancamento na massa de solo, simulando assim,
camadas
horizontais de reforço ao serem solicitadas ao cisalhamento por uma superfície
potencial de ruptura de um talude ou uma estrutura de contenção que se movimenta.
69
Figura 30- Esquema ilustrativo do ensaio de cisalhamento direto com reforço
inclinado
Fonte: ( Abramneto apud Teixeira, 2003).
d-) Ensaio de Tração confinada com solo: McGown et al., (1982) citado por
Texeira (2003) apresentou este tipo de ensaio, que consiste na combinação dos
ensaios de tração e de arrancamento e se presta ao estudo do comportamento da
relação entre força e deformação de reforços em meio a um solo e submetidos a
uma tensão de confinamento. Este tipo de teste pode ser executado em um
equipamento de ensaios de arrancamento, desde que a extremidade final da
amostra de geossintético seja fixada em uma estrutura indeslocável na parte
posterior da caixa de ensaios. A Figura 31 ilustra esquematicamente o ensaio.
Os resultados dos ensaios têm aplicação principalmente quando se deseja
estudar o comportamento força vs. deformação de alguns geossintéticos, em
especial geogrelhas em meio a um solo arenoso ou pedregulhoso, onde ocorre o
imbricamento de partículas em meio às aberturas da grelha. O comportamento força
vs. deformação do conjunto solo–geogrelha é bastante influenciado pelo
imbrcamento das partículas de solo e diferente sensivelmente do comportamento
não confinado.
70
Figura 31 - Esquema do ensaio de tração confinada com solo
Fonte: (Lo apud Teixeira, 2003).
71
4. PROJETO DE ATERRO REFORÇADO SOBRE SOLO MOLE
4.1.
GENERALIDADES
A técnica de solo reforçado consiste na introdução de elementos resistentes à
tração, convenientemente orientados, que aumentam a resistência e diminuem a
deformabilidade do maciço. Neste método, designado por reforço de solos, o
comportamento global do maciço é melhorado à custa da transferência de esforços
para os elementos resistentes.
Figura 32 - Elementos de Solo Com e Sem Reforço
Fonte: (adaptada de Abramento, 1998)
72
Atualmente com relação a aterros, segundo a BS 8006, existem duas áreas
de aplicação:
a)
Fundações de aterros sobre solos moles e muito moles;
b)
Aterros sobre áreas propensas a subsidência.
Os estados limites últimos ( 120 anos ) considerados pela BS 8006 são:
a) Estabilidade local do material de aterro;
b) Estabilidade rotacional do material de aterro;
c) Estabilidade de deslizamento lateral do material de aterro;
d) Estabilidade de extrusão da fundação;
e) Estabilidade global.
Figura 33 - Estado limite ultimo para a base o aterro reforçado
Fonte : ( Maccaferri, adaptado de BS8006)
Os estados limites de servicibilidade a serem considerados são:
a) Tensão excessiva no reforço;
b) Recalque da fundação.
73
Figura 34 – Estado limite de utilização ( servicibilidade ) para aterros com base
reforçado.
Fonte : (Maccaferri, adaptado de BS8006)
Uma importante consideração é aquela na qual estabilidade do aterro é mais
crítica durante a sua construção. Isto se deve à relativa baixa permeabilidade do
solo mole que não permite a completa consolidação durante o período de
construção. Ao final da construção a carga do aterro foi totalmente aplicada, mas o
ganho da resistência ao cisalhamento do solo de fundação devido à consolidação
pode ser insuficiente para garantir a estabilidade.
Uma vez ocorrida a consolidação, a melhoria resultante da resistência ao
cisalhamento do solo da fundação irá remover a necessidade do uso de reforços
para melhorar a estabilidade. Deste modo durante o período entre o final da
construção e a consolidação da fundação o requerimento fundamental de resistência
do reforço é aquele de garantir, em qualquer instante neste intervalo, que a
resistência de projeto se iguale ou supere a carga de projeto.
O reforço da base estabiliza um aterro sobre solo mole através da prevenção
da ruptura lateral do aterro, da extrusão (ruptura) do solo de fundação e da ruptura
global. Esta força estabilizante é gerada no reforço através da tensão de
cisalhamento transmitida do solo de fundação e do aterro que colocam o reforço em
tensão.
A força de tração máxima Tr, no estado limite, a ser resistida pelo reforço na
base do aterro deve ser o maior que:
74
- máxima força de tração necessária para resistir ao estado limite de rotação Tro
por metro linear; ou
- a soma da máxima força de tração necessária para resistir o deslizamento
lateral Tds por metro linear e a máxima força de tração necessária para resistir à
extrusão da fundação Trf, por metro linear.
Para assegurar que o estado limite último que governa a ruptura do reforço não
será atingido durante a vida de projeto do reforço, a seguinte condição deverá ser
observada:
K…
*•
≥ &
( 22)
Onde:
&' = é a resistência de projeto do reforço;
( = é o fator parcial para ramificações econômicas de colapso, ver tabela 9.
Para assegurar que o estado limite último da força de tração poderá se
desenvolver ao longo do reforço de base uma ancoragem adequada será necessária
entre o reforço e o solo adjacente. Para cada estado limite, forças de tração devem
ser determinadas (Tro, Tds e Trf) as ancoragens associadas aos reforços devem
também ser verificadas para assegurar que o estado limite de carga poderá ser
gerado no reforço.
As deformações desenvolvidas nos reforços não devem exceder os valores
pré-determinados através de considerações do estado limite de serviciabilidade
(utilização), ver figura 34. Deformações no reforço devem ser determinadas a partir
das cargas aplicadas. Existem outros mecanismos, tal como processos construtivos
que podem induzir deformações ao reforço; estas deformações são difíceis de
quantificar.
Como regra geral a máxima deformação εmax no reforço de base não deve
exceder 5% para aplicações de curto prazo e 5% a 10% para condições de longo
prazo. As observações mostraram que os aterros reforçados apresentaram um bom
comportamento com estes valores limites.
Onde os aterros reforçados são construídos sobre solos de fundação moles e
compressíveis, a deformação máxima admissível no reforço deve ser reduzida para
garantir a compatibilidade com o solo de fundação.
75
Para a construção de aterros reforçados sobre solos moles e muito moles as
técnicas em uso podem ser classificadas em uma de duas categorias:
Aquelas técnicas onde o reforço é utilizado para o controle inicial da
estabilidade do aterro, sem controle de recalques, ver figura 35;
Figura 35 - Reforço utilizado para controlar somente a estabilidade inicial do aterro.
Fonte : (Maccaferri, adaptado de BS8006).
Aquelas técnicas onde o reforço é utilizado como parte do sistema de
estabilização da fundação para o controle da estabilidade e prevenção de recalques
do aterro, ver figura 36.
Figura 36 - Reforços utilizados para controle somente de estabilidade inicial e
recalque do aterro.
Fonte : (Maccaferri, adaptado de BS8006)
O primeiro estágio do projeto, normalmente é a determinação de uma
geometria consistente para o aterro, com sua estabilidade definida a longo prazo
utilizando métodos convencionais. A tensão de cisalhamento do aterro e do solo de
fundação pode ser modelada usando os parâmetros apropriados c´ e ϕ´, em termos
76
de tensões efetivas, já fatorados e com as devidas considerações de longo prazo
para regimes de poro-pressão atuando no aterro ou no solo de fundação.
Nos casos onde o solo de fundação é muito mole, taludes laterais com
geometria baseada em análises de estabilidade de longo prazo, podem ser muito
íngremes, se analisado em condições de curto prazo, mesmo com a inclusão de
reforços. Nesta situação o talude deve ser suave para satisfazer as condições de
estabilidade de curto prazo e então re-analisado para a condição de longo prazo
para assegurar que aquelas condições de estabilidade serão atingidas.
4.2.
FATORES PARCIAIS
Formatado: Nível 2
Muitas das análises e projetos de solos reforçados utilizam o método do
equilíbrio limite, no qual um fator de segurança global deve ser satisfeito. Como
estes métodos são baseados em considerações de equilíbrio eles podem ser
simplesmente redefinidos na forma de um estado limite pelo acréscimo do peso de
solo e cargas atuantes através de fatores parciais de carga apropriados ou
reduzindo as propriedades dos solos e de resistência dos reforços com o uso de
apropriados fatores parciais relacionadas ao tipo do material.
Tabela 9 - Resumo dos fatores parciais de segurança para serem utilizados em
projetos de aterros reforçados sobre solo mole
Fonte: ( Maccaferri adaptado deBS8006 )
Estado limite
último
Estado limite
de utilização
ffs = 1.3
ffs = 1.0
ff = 1.2
ff = 1.0
fq = 1.3
fq = 1.0
para ser aplicado para tan ϕ´cv
fms = 1.0
fms = 1.0
Para ser aplicado para c´
fms = 1.6
fms = 1.0
para ser aplicado para cU
fms = 1.0
fms = 1.0
Fatores parciais
Fatores de
Carga
Fatores do
tipo de solo
Fatores do
tipo de
reforço
Fatores de
interação
solo/reforço
Peso específico dos solos, ex. altura
dos aterros.
Linha de cargas externas fixas, ex.
linha ou ponto de carga
Linha de carga externa móveis, ex.
carregamento de tráfego
para ser aplicado para resistência
nominal do reforço
ASPECTOS RELATIVOS AOS
REFORÇOS – FATORES DE
REDUÇÃO (ITEM 4.2.1.)
Deslizamento através da superfície do
reforço
fs = 1.3
fs = 1.0
Resistência do reforço ao pull-out
fp = 1.3
fp = 1.0
77
O fator parcial para o material do solo, que leva em consideração a resistência
do reforço a longo prazo, é também especificado pela BS 8006. O fator parcial para
o material, $ , é calculado como segue abaixo:
$ = $)) ∙ $) ∙ $) ∙ $
(23)
onde:
$)) é um fator parcial do material relativo a consistência de fabricação do
reforço e como a resistência pode ser afetada por isso e possível imprecisão nesta
avaliação;
$) é um fator parcial do material relativo a extrapolação dos ensaios
procedendo com a resistência de base;
$) é um fator parcial do material relativo a susceptibilidade do reforço a
danos de instalação;
$ é um fator parcial do material relativo ao ambiente no qual o reforço é
instalado.
4.2.1. ASPECTOS RELATIVOS AOS REFORÇOS – FATORES DE
REDUÇÃO
Um projeto envolvendo materiais geossintéticos deve considerar três tipos de
propriedades: propriedade requerida, propriedade índice e propriedade funcional.
A propriedade requerida está associada ao valor da função especificada no
projeto para efeito de dimensionamento. A partir da propriedade requerida, procedese à escolha do geossintético que melhor se aplica ao projeto. Os produtos capazes
de atender às propriedades requeridas podem ser posteriormente submetidos a
ensaios, para possibilitar o dimensionamento final.
As propriedades índice são obtidas a partir de ensaios de caracterização e
geralmente são fornecidas pelo fabricante. Estas propriedades são inerentes ao
produto e não consideram objetivo determinar as características básicas do produto
e possuem procedimentos estabelecidos em norma, tratando-se, em geral, de
ensaios rápidos e simples.
78
A propriedade funcional deve levar em consideração o tipo de solicitação
imposta na obra e as condições de utilização do geossintético. Esta propriedade
representa o comportamento do geossintético sob as condições de utilização
impostas pela obra e permite considerar a interação com o meio adjacente.
A propriedade funcional (&- ) de um determinado geossintético pode ser
determinada pela razão entre a propriedade índice (&. ) e o fator de redução total ( ).
O fator de redução total ( ) é dado pelo produto dos fatores de redução parciais,
definidos por função e tipo de aplicação.
No caso de obras de solo reforçado com geossintéticos, os principais fatores
de redução a serem considerados são:
• Fator de redução devido a deformações por fluência (* );
• Fator de redução devido à degradação química e biológica pelo meio
ambiente (+ );
• Fator de redução devido a eventuais emendas (, );
• Fator de redução devido a danos mecânicos (' );
Neste caso, a propriedade funcional é dada pela expressão:
&- =
K—
*˜ ∙*™ ∙*š ∙*…
(24)
Os fatores de redução indicam a razão entre a propriedade índice e a
propriedade funcional sob condições específicas de projeto. O fator de redução total
é composto pelo conjunto dos fatores de redução parciais obtidos para cada
condição. A análise de sistemas de solo reforçado tem adotado os fatores de
redução parciais (ou fatores de segurança parciais), ao invés de um único fator de
segurança total, como é usual em outras áreas da Geotecnia. O motivo da adoção
de fatores de redução parciais deve-se às inúmeras variáveis que intervêm nas
propriedades mecânicas dos reforços em condições de serviço.
Os fatores de redução dependem basicamente das características do
geossintético e das características do ambiente onde o geossintético será instalado.
Dentre as características dos geossintéticos, pode-se citar o tipo e a natureza do
polímero e o processo de fabricação. Em relação às características do ambiente,
destacam-se o tipo de aplicação do geossintético, ou seja, a função desempenhada,
o tipo de obra e o processo de instalação.
79
Segundo Koerner (1998), citado em Santos (2008), os valores sugestivos de
fatores de redução em função do tipo de aplicação para geogrelhas em Aterros
Reforçado sobre solos moles, é:
' = 1.1 a 1.4
* = 1.6 a 3.0
+ = 1.0 a 1.8
Na Tabela 10, são propostos fatores de redução em função do tipo de polímero
constituinte.
Tabela 10 - Fatores de Redução em Função do Tipo de Polímero
Fonte: (Santos, 2008 , apud Vidal et al,1999)
França
Alemanha
*
'
+
)
, PET
PP, PE
PET
PP, PE
2.5
5.0
2.5
5.0
1.5
1.5
1.05
2.0
1.0
1.0
Legenda: PET: poliéster PP: polipropileno PE: polietileno
¹ (sem impacto ambiental) ; ² (sem emendas)
4.2.1. FATOR DE REDUÇÃO DEVIDO A FLUÊNCIA
A fluência pode ser definida como a aptidão de um material ao alongamento,
quando submetido a um carregamento estático de longa duração. A magnitude das
deformações por fluência depende da composição do polímero e da estrutura das
fibras. O geossintético, quando submetido a uma carga de tração constante, leva um
determinado intervalo de tempo para atingir a ruptura por fluência. A resistência do
geossintético a ser utilizada no dimensionamento de um aterro reforçado deve ser
baseada na expectativa da resistência do material ao final da vida útil da obra.
Em geral, o fator de redução por fluência é definido pela razão entre a carga de
ruptura convencional (obtida em ensaios de tração simples) e a carga que leva à
ruptura do geossintético por fluência.
80
4.2.2. FATOR DE REDUÇÃO DEVIDO A DEGRADAÇÃO
PELO MEIO AMBIENTE
O meio ambiente pode produzir a degradação dos geossintéticos ao longo de
sua vida útil. A degradação ambiental manifesta-se através dos mecanismos de
degradação química e biológica. Estes mecanismos atuam continuamente ao longo
do tempo de serviço do reforço. A degradação química compreende a transformação
estrutural dos polímeros, resultante da ação de substâncias quimicamente ativas
presentes no solo.
Os principais mecanismos de degradação química são a termo-oxidação, a
foto-oxidação e a hidrólise, onde a seguir serão comentadas suas principais
características.
A termo-oxidação é o mecanismo de oxidação ativado pelo calor. Em
temperaturas normais de utilização em Geotecnia, os polímeros comumente
empregados nos geossintéticos não apresentam, em geral, problemas de
estabilidade. No entanto, sob temperatura elevada, algumas propriedades
mecânicas podem sofrer alteração ao longo do tempo, especialmente a relação
tensão-deformação.
A foto-oxidação é um mecanismo oxidante ativado pela radiação ultravioleta. A
ação da radiação UV atinge apenas a superfície das fibras, tornando-as quebradiças
e com menor resistência.
A hidrólise consiste na ruptura das cadeias moleculares pela ação das
moléculas de água. O processo de hidrólise pode ocasionar uma perda de massa
molecular do polímero para o meio em que se encontra e uma erosão superficial das
fibras do geossintético. A conseqüência desse processo é a perda de resistência por
enfraquecimento das fibras que compõem o produto.
A oxidação provoca a corrosão das fibras do geossintético causando sua
ruptura, e consequentemente, a redução de suas propriedades. Já a degradação
biológica é resultante da atividade de microorganismos (bactérias e fungos), que
podem eventualmente se agregar à superfície dos geossintéticos.
81
4.2.3. FATOR DE REDUÇÃO DEVIDO A EMENDAS
As emendas em geossintéticos podem ser executadas através de 4 processos:
solda ou colagem, travamento simples, superposição de camadas ou costura. A
presença de emendas gera uma região menos resistente. Para os processos de
solda, costura e travamento, os fatores de redução devido a emendas são obtidos
através de ensaios de tração em emendas. Em geral, o fator de redução devido a
emendas varia entre 1.0 e 1.2.
4.2.4. FATOR
DE
REDUÇÃO
DEVIDO
A
DANOS
MECANICOS
O dano mecânico pode ser definido como a transformação da estrutura do
geossintético causada por esforços durante o manuseio e instalação do material e
durante a compactação do solo sobrejacente.
No caso de maciços reforçados, o fator de redução por danos de instalação
(danos mecânicos) prepondera sobre os demais. A ocorrência do dano mecânico é
maior quando são empregados solos de granulometria grosseira e métodos de
compactação mais agressivos. Quanto maior a intensidade do dano mecânico, maior
o fator de redução.
Durante o processo de instalação, o geossintético pode sofrer danos
provocados pela compactação, tráfego de veículos, lançamento de agregados
pontiagudos, rasgos, etc.
Estes danos podem reduzir significativamente as propriedades mecânicas do
produto. A Tabela 11 apresenta faixas de valores para o fator de redução por dano
mecânico em função da capacidade de sobrevivência do geossintético e da
severidade do ambiente de instalação.
82
Tabela 11 - Faixa de Fatores de Dano para Geogrelhas
Fonte: ( Manual Maccaferri Simplificado para Aplicação em Geossintéticos adaptado
de Azambuja, 1994 )
Severidade do Meio
Capacidade de
Geossintético sobrevivência
Baixa
Moderada
Alta
Muito alta
Geogrelha
flexível-acrilico
Geogrelha
flexível- PVC
Geogrelha
rígida
de polipropileno
Geogrelha
rígida
de polietileno
Moderada
1.10 – 1.20
1.20 – 1.40
NR
NR
Alta
1.10 – 1.15
1.20 – 1.40
1.50 – NR
NR
Moderada
1.05 – 1.15
1.15 – 1.30
1.40 – 1.60
NR
Alta
1.05 – 1.15
1.15 – 1.30
1.40 – 1.60
1.50 – 2.00
Moderada
1.05 – 1.15
1.05 – 1.20
1.30 – 1.45
NR
Moderada
1.05 – 1.15
1.10 – 1.40
1.20 – 1.50
1.30 – 1.60
Alta
1.04 – 1.10
1.05 – 1.20
1.15 – 1.45
1.30 – 1.50
O termo “capacidade de sobrevivência” é utilizado para descrever a resistência
à destruição do geossintético diante dos esforços decorrentes do processo
construtivo e das solicitações iniciais da obra. Os critérios de classificação da
capacidade de sobrevivência das geogrelhas registrados na literatura estão
resumidos na Tabela 12.
Os ambientes de instalação são classificados segundo a agressividade ou
severidade do meio. Allen (1991), citado por Manual Maccaferri Simplificado para
Aplicação em Geossintéticos, propõe critérios de classificação da severidade do
ambiente em função das condições de instalação do geossintético em sistemas de
contenção (Tabela 13), porém podendo assim ser utilizado para aterros reforçados
sobre solos moles com geogrelhas. Esta classificação é função da espessura da
camada de solo sobrejacente ao geossintético, da forma e da dimensão dos grãos
de solo e do tipo de equipamento utilizado na compactação.
83
Tabela 12 - Critério para Classificação da Capacidade de Sobrevivência de
Geossintéticos
Fonte: (Manual Maccaferri Simplificado para Aplicação em Geossintéticos adaptado
de Azambuja, 1994).
Geogrelhas
Capacidade
Sobrevivência
Flexíveis
Rígidas
Baixa
-
-
Moderada
T ≤ 55
T < 55
Alta
T > 55
T ≥ 55
T = resistência à tração (kN/m²)
Tabela 13 - Classificação da Severidade do Meio
Fonte: ( Manual Maccaferri Simplificado para Aplicação em Geossintéticos adaptado
de Azambuja, 1999)
Espessura da Camada
Tipo de
Aterro
Equipamento
< 15cm
15-30cm
> 30cm
leve
e
rebocado
areia fina a grossa com
grãos
sub-arredondados
baixa
baixa
baixa
areia e cascalho bem
graduados com grãos
de subarredondados
a subangulares,
∅$+ < 75mm
moderada
baixa
baixa
muito alta
alta
moderada
moderada
baixa
baixa
areia e cascalho bem
graduados com grãos
de subarredondados
a subangulares,
∅$+ < 75mm
alta
moderada
baixa
cascalho mal graduado
com
grãos angulosos,
∅$+ < 75mm
NR
muito alta
alta
cascalho mal graduado
com
grãos angulosos,
∅$+ < 75mm
areia fina a grossa com
grãos
sub-arredondados
pesado
e
autopropelido
84
4.3.
ESTABILIDADE LOCAL
A estabilidade local dos taludes laterais do aterro (ver figura 33a) deve ser
Formatado: Nível 2, Vários níveis +
Nível: 2 + Estilo da numeração: 1, 2, 3,
… + Iniciar em: 2 + Alinhamento:
Esquerda + Alinhado em: 2,01 cm +
Recuar em: 3,28 cm
verificada da seguinte forma:
Œ
ž;
<
5¡ ¢=B
(25)
*_;
Onde:
H
=
é a altura total do aterro;
/
=
é o comprimento horizontal do talude lateral do aterro;
n′
=
é o ângulo de atrito do aterro a grandes deformações sob
condições de tensões efetivas;
$
=
é o fator parcial de segurança para o material aplicado ao valor
tang φ’cv, ver tabela 9.
4.4.
ANÁLISE DE SUPERFÍCIES DE DESLIZAMENTO
A análise de superfícies de deslizamento é a técnica mais comum utilizada
para analisar a estabilidade rotacional de aterros reforçados. Os princípios gerais
envolvidos são mostrados na figura 37.
O procedimento envolve a análise de superfícies de deslizamento, buscando
ao longo da base do aterro, a posição (ou local) da carga no reforço que é
necessário prover uma margem de estabilidade adequada (ver figura 37), de forma
que Linha de ruptura seja um arco de circunferência.
Para a verificação o reforço é considerado como um momento estabilizante
adicional que promove a estabilidade global do aterro, e a resistência do reforço Troj
necessária por metro linear em qualquer local, j, ao longo da base do aterro (ver
figura 37a) e deve ser determinada a partir de:
Troj .Y j = M RRj = M Dj − M RSj
Onde:
(26)
Formatado: Nível 2, Vários níveis +
Nível: 2 + Estilo da numeração: 1, 2, 3,
… + Iniciar em: 2 + Alinhamento:
Esquerda + Alinhado em: 2,01 cm +
Recuar em: 3,28 cm
85
Yj
=
é o braço do momento vertical para a superfície crítica no local j
ao longo da base do aterro;
MRRj
=
é o máximo momento resistente devido ao reforço em um local j
ao longo da base do aterro;
MDj
=
é o máximo momento atuante fatorado em um local j ao longo da
base do aterro;
MRSj
=
é o máximo momento resistente fatorado devido ao solo em um
local j ao longo da base do aterro.
Um gráfico dos valores de Troj através base do aterro determinam o local das
forças mostradas na figura 37a. A máxima resistência necessária para o reforço Tro
é obtida onde Troj alcança um valor máximo.
Para a maioria das geometrias dos aterros é necessário executar análises de
superfícies de deslizamento em um dos lados do aterro somente para checar ao
valor do Tro.
Porém para aterros muito baixos e largos, as análises das superfícies de
deslizamento podem ter que continuar além da linha de centro do aterro a fim de
determinar Tro.
O reforço deve alcançar uma ancoragem adequada com o solo adjacente para
assegurar que a carga Troj seja mobilizada. Esta ancoragem deveria ser atingida ao
longo do reforço em ambos os lados da linha que define a potencial superfície de
deslizamento (dentro e além dela), ver figura 37b. Dentro da superfície de
deslizamento temos:
f n . f p .Troj ≤ γ .h.
α ' . tan ϕ cv'
f ms
⋅ Lj +
α bc '.Cu
f ms
⋅ Lj
(27)
Onde:
fn
=
é o fator de segurança parcial que governa as ramificações
econômicas do mecanismo de falha, ver tabela 9;
fp
=
é o fator de segurança parcial aplicado à resistência do reforço
ao pull-out (arrancamento), ver tabela 9;
Troj
=
é a carga no reforço por metro, necessária para manter a
estabilidade no ponto j ao longo da base do aterro;
86
γ
=
é o peso específico do material que forma o aterro;
h
=
é a altura média do aterro sobre o reforço ao longo do
comprimento Lj;
α’
=
é o coeficiente de interação solo/ângulo de adesão do reforço
=
é o ângulo de atrito do aterro a grandes deformações sob
tang φ’cv;
φ’cv
condições de tensões efetivas;
fms
=
é o fator parcial de segurança para o material aplicado ao valor
tang φ’cv e Cu, ver tabela 9;
Lj
=
é o comprimento de ancoragem necessário para o reforço, por
metro, dentro do arco que define a superfície de ruptura;
αbc’
=
é o coeficiente de interação solo/adesão do reforço com Cu.
Cu
=
é a resistência não drenada do solo mole que forma a fundação
adjacente ao reforço.
O comprimento de reforço necessário além da linha que define a superfície de
deslizamento pode ser determinada substituindo B-Lj por Lj na equação acima, onde
B é o comprimento total do reforço no aterro, ver figura 37b.
87
Momento solicitante devido ao solo e carregamentos:
M D = [∑ ( f fs .Wi + f q .bi .wsi ).sin α i ].Rd
Momento estabilizante devido ao solo:
'
 c'

tan ϕ cvi
M RS = [∑  i ⋅ bi . secα i + ((Wi + bi .wsi ). cos α i − ui .bi . secα i ).
].Rd
f ms 
 f ms
Momento estabilizante devido ao reforço:
M RR = Tro .Y
a) Princípios que governam o uso do método de análise de superfícies de deslizamento para
determinar a máxima tensão necessária em um reforço de base de um aterro.
Figura 37- Procedimento para avaliar a estabilidade rotacional através de análises
de superficies circulares de deslizamento.
Fonte : (Maccaferri, adaptado de BS8006 ).
88
4.5.
DESLIZAMENTO LATERAL
A estabilidade contra o deslizamento lateral do aterro, ver figura 33c, deve
considerar qualquer possível superfície de deslizamento que se desenvolva entre o
aterro e a superfície superior do reforço na base.
O reforço na base é necessário para resistir o empuxo horizontal externo (para
fora) do aterro.
A carga no reforço é máxima na extremidade da crista do aterro, ver figura 38.
Esta carga no reforço Tds vale:
Tds = 0,50.K a .( f fs .γ .H + 2. f q .ω s ).H
(28)
Onde:
Tds
=
é a carga de tração no reforço por metro, necessária para resistir
ao empuxo lateral gerado pelo aterro;
(
)
Ka
=
é o coeficiente de empuxo ativo [ = tan 2 45 o − ϕ ' cv 2 ];
H
=
é a altura do aterro;
γ=
é o peso específico do material que forma o aterro;
ωs
=
é a intensidade da sobrecarga externa no topo do talude;
ffs
=
é o fator parcial de segurança para o peso específico do solo,
=
é o fator de segurança parcial para as cargas externas
ver tabela 9;
fq
aplicadas, ver tabela 9.
Para gerar a carga de tração Tds no reforço, o aterro não deve deslizar fora do
reforço. Para prever este deslizamento horizontal o comprimento de reforço mínimo
Le deverá ser:
Le ≥
0,50.K a .H .( f fs .γ .H + 2. f q .ω s ). f s . f n
γ .h.
Onde:
α ' . tan ϕ cv'
f ms
(29)
Formatado: Nível 2, Vários níveis +
Nível: 2 + Estilo da numeração: 1, 2, 3,
… + Iniciar em: 2 + Alinhamento:
Esquerda + Alinhado em: 2,01 cm +
Recuar em: 3,28 cm
89
fs =
é o fator de segurança parcial para a resistência ao deslizamento do
reforço, ver tabela 9;
fn
é o fator de segurança parcial que governa as ramificações
=
econômicas do mecanismo de falha, ver tabela 9;
h
é a altura média do aterro sobre o reforço ao longo do
=
comprimento Le;
α’
=
é o coeficiente de interação solo/ângulo de adesão do reforço
para tang φ’cv;
φ’cv
=
é o ângulo de atrito do aterro a grandes deformações sob
condições de tensões efetivas;
fms
=
é o fator parcial de segurança para o material aplicado ao valor
tang φ’cv, ver tabela 9;
Figura 38 - Estabilidade lateral na Interface do aterro.
Fonte : (Maccaferri, adaptado de BS8006 ).
4.6.
EXPULSÃO DA FUNDAÇÃO
A geometria do aterro induz uma tensão de cisalhamento para fora no interior
da camada de solo mole da fundação. Onde o solo de fundação é muito mole e de
profundidade limitada a força cisalhante para fora pode provocar a expulsão do solo
da fundação (ver figura 33d). Para prevenir esta expulsão o comprimento do talude
lateral do aterro Ls tem que ser grande suficiente para evitar a mobilização destas
forças de cisalhamento para fora.
Formatado: Nível 2, Vários níveis +
Nível: 2 + Estilo da numeração: 1, 2, 3,
… + Iniciar em: 2 + Alinhamento:
Esquerda + Alinhado em: 2,01 cm +
Recuar em: 3,28 cm
90
O mecanismo de falha assume a expulsão do solo de fundação abaixo do
aterro, ver figura 39. Para prevenir a ocorrência deste estado limite é necessário
limitar o movimento da fundação para fora, através do desenvolvimento de um
adequado confinamento lateral sobre uma área de superfície suficientemente grande
em contato com o lado inferior do reforço de base. Para que estas duas condições
sejam satisfeitas. Primeiramente a resistência ao cisalhamento global no lado inferior
do reforço deve ser suficiente para resistir o desenvolvimento das cargas laterais no
solo de fundação. E em segundo lugar o reforço de base deve ter resistência
suficiente para absorver as cargas induzidas pelas forças de cisalhamento e
transmitidas para o solo de fundação.
Para prevenir a expulsão da fundação a seguinte relação deve ser aplicada, ver
figura 39a:
Rha = Rhp + Rs + RR
(30)
Onde:
Rha
=
é força horizontal fatorada que causa a expulsão do solo de
=
é força horizontal fatorada devida à resistência passiva do solo
=
é força horizontal fatorada devida à resistência ao cisalhamento
fundação;
Rhp
de fundação;
Rs
do solo de fundação a uma profundidade zc;
RR
=
é força horizontal fatorada devida à resistência ao cisalhamento
do solo de fundação no lado inferior do reforço;
Uma análise refinada utilizando diferentes valores de zc é realizada para
determinar o mínimo comprimento de ancoragem Ls necessário para prevenir a
expulsão da fundação.
É prática comum executar análises utilizando parâmetros não-drenados do
solo. Se o solo mole tem um limite de profundidade e tem resistência não drenada
constante com a profundidade, usa-se então a relação indicada na figura 39b
91
indicando o comprimento de ancoragem mínimo necessário Ls a ser determinado
como segue:

4C
 f fs .γ 1.H + f q .ω s − u
f ms
Ls ≥ 
'
1 + α bc .Cu
f ms
(
)

.z c

(31)
Onde:
ffs
=
é o fator parcial de segurança para o peso específico do solo,
=
é o fator de segurança parcial para as cargas externas
ver tabela 9;
fq
aplicadas, ver tabela 9;
γ1
=
é o peso específico do material que forma o aterro;
H
=
é a máxima altura do aterro;
ωs
=
é a intensidade da sobrecarga externa no topo do aterro;
Cu
=
é a resistência não drenada do solo mole que forma a fundação;
fms
=
é o fator parcial de segurança para o material aplicado ao valor
Cu, ver tabela 9;
=
zc
é a profundidade da camada de solo mole quando a fundação
tem uma espessura definida e resistência não-drenada constante com a
profundidade;
αbc’
=
é o coeficiente de interação solo/adesão do reforço com Cu.
A carga de tração gerada no reforço da base Trf por metro linear devido à
tensão de cisalhamento “para fora” da fundação será:
Trf =
α bc ' .C uo .Le
f ms
(32)
Onde:
Le
=
é o comprimento do reforço, ver figura 39;
92
Cuo
=
é a resistência não drenada do solo de fundação abaixo do
=
é o fator parcial de segurança para o material aplicado ao valor
reforço;
fms
Cu, ver tabela 9;
É necessário cuidado na escolha do valor de αbc´, o coeficiente de interação
reforço/solo de fundação. A magnitude de αbc´ está relacionada não somente às
características da superfície do reforço, mas também à deformação do reforço
comparada com a deformação do solo de fundação. A compatibilidade de
deformações entre o reforço e o solo mole da fundação é necessária a fim de se
atingir o máximo coeficiente de adesão. Isto é particularmente o caso quando se lida
com solos de fundação compressíveis e amolgados onde a deformação no reforço
não deve exceder a deformação que corresponde ao pico de resistência não
drenada mobilizada no solo de fundação.
93
Figura 39 - Analise de estabilidade contra a expulsão do solo de fundação
Fonte : (Maccaferri, adaptado de BS8006).
94
4.7.
ESTABILIDADE GLOBAL
Para aterros executados sobre camadas profundas de solo muito mole, a
estabilidade global deve ser verificada para garantir que mecanismos de falha
profundos não possam ocorrer (ver figura 32), onde um fator de segurança deve ser
satisfeito.
Esse tipo de superfície de ruptura pode ser determinado através do método de
Meyerhof (ver figura 40)
Ângulo de aplicação do empuxo ativo (£) )
£) = 45 b
n
2
Ângulo de aplicação do empuxo Passivo (£ )
£ : 45 Z
n
2
Raio de aplicação do Empuxo Ativo ( ¤))
¤) : ∙
7¡ ¥Q
7¡ ¦
,
sendo: § : 90 Z n
Raio de aplicação do Empuxo Passivo
¤ : ¤ ∙ % >)t@∩RD∙ 5¡ ¢ , sendo: ¤ : ¤) ∙ %>Z∩1 ∙tan nD
∩) : 180 Z £) Z §
∩ : § Z £
Figura 40 – Metodo de Meyerhof para estabelecer superfície critica de ruptura de
fundação
Fonte : ( Adaptado de Cintra, 2003 )
Formatado: Nível 2, Vários níveis +
Nível: 2 + Estilo da numeração: 1, 2, 3,
… + Iniciar em: 2 + Alinhamento:
Esquerda + Alinhado em: 2,01 cm +
Recuar em: 3,28 cm
95
Após estabelecido a superfície critica pode ser determinado o fator de
segurança através do método das lamelas.
Levando em conta que a massa de solo seja dividida em lamelas e o equilíbrio
de forças envolve o peso “W” da lamela, e as forças resultantes de pressões neutras
“U” e forças normais “N” e tangenciais “T” ( ver figura 41 )
Figura 41 – método das Lamelas
Fonte : ( Santos, 2008 ).
As lamelas de forma individual são submetidas aos esforços de Empuxo “E”,
Esforço cisalhante “X”, Força normal “N” e Força tangencial “T” ( ver figura 42 ).
96
Figura 42 – Lamela de forma individual
Fonte : ( Santos, 2008).
Onde:
T =
A força que mede a resistência mobilizada, que é uma fração da
resistência total ao cisalhamento, sendo dada por:
ℓ =
É o comprimento da base da lamela
 =
É a força normal “efetiva” atuante na base da lamela.
F =
Coeficiente de segurança referente à relação entre a resistência ao
cisalhamento do solo (s) e a tensão cisalhante atuante ( ) é obtida através da
equação de equilíbrio:
T
©=ª
(33)
Sendo:
= . ℓ
(34)
97
4.7.1.4.2.2. METODO DE BISHOP SIMPLIFICADO
Segundo o método de Bishop simplificado, levando em consideração a
interação entre as varias lamela o equilíbrio das forças se dá na direção vertical,
conforme figura 43, onde para este tipo de analise um fator de segurança deverá ser
satisfeito.
Figura 43 – Forças atuantes em uma lamela segundo o método de Bishop
simplificado.
Fonte : ( Santos, 2008 ).
Onde:
(
+ Š) ∙ cos ­ b & ∙ sin ­ : ¯
(35)
e
:
=± ∙∆²∙³´µ ¶
·
³´µ º± ∙»¼µ ¶
3¸ ¹}
·
°@∙∆@
(36)
O processo de calculo para determinação do fator de segurança contra a
ruptura, deve ser estabelecido através de um processo interativo, pois
função de F, onde através da equação abaixo :
esta em
98

c'.∆x.tgθ

P − u.∆x −


F
∑' c'.l +
.tgφ 
tgφ '.senθ


cos θ +

F

F=
∑( P.senθ )
(37)
O cálculo iterativo do coeficiente de segurança F é feito da seguinte forma:
a) Adota-se um valor inicial F1, entra-se na expressão acima (37), extraindo
um novo fator de segurança F2, que é comparado a F1.
b) Se a precisão escolhida não for atingida, extrai-se um novo valor do fator de
segurança F3 e assim por diante, até a precisão desejada
c) Em geral três iterações são necessários
4.8.
VERIFICAÇÃO DO RECALQUE
Para solos sobre adensados a estimativa dos Recalques finais podem ser
determinados através da Teoria Unidimensional de Terzagui, sendo:
ρ=
¾
)}¿
∙ ÀC2 ∙ log
Á´
¼
Â
+ C3 ∙ log à Ä
Á
´
Onde:
H = Espessura da Camada de solo mole
e = Índice de vazios do solo
C2 = Índice de recompressão
C3 = Índice de Compressão
P5 = Tensão de Pré-adensamento
σ7 = Tensão inicial ( referente a metade da camada de solo mole)
σ8 = Tensão após a construção do aterro
(38)
Formatado: Nível 2, Vários níveis +
Nível: 2 + Estilo da numeração: 1, 2, 3,
… + Iniciar em: 2 + Alinhamento:
Esquerda + Alinhado em: 2,01 cm +
Recuar em: 3,28 cm
99
Este recalque deve ser acrescido do Recalque imediado, dado pela teoria da
elasticidade.
Ç. = ∙
AC ∙È
É
∙ (1 − Ê )
(39)
Onde:
Ç. = Recalque Inicial
= Coeficiente de Forma
= Tensão do Aterro uniformemente distribuída
Ë = Largura da área carregada
= Parâmetro elástico do solo mole.
Ê = Parâmetro elástico do solo mole.
Levando em consideração que a pressão neutra não se dissipa uniformemente
ao longo de toda a profundidade, após verificado o Recalque, é possível determinar,
o tempo de adensamento ao longo da profundidade, qual é determinada pela
equação abaixo:
Ì=
Í∙Î{ Ï
ÐÑ
(40)
Onde:
= Tempo em que ocorrerá o Recalque
& = Fator tempo, em função do grau de adensamento (U) Fornecido pela
Tabela)
= Coeficiente de adensamento
9' = Altura referente a metade da espessura da camada de solo mole
U = Grau de adensamento ao longo da profundidade
100
Figura 44 – Curva de adensamento
Fonte : ( Souza Pinto, 2001)
Tabela 14 – Fator tempo em função da porcentagem de recalque para adensamento
pela teoria de Terzaghi
Fonte : ( Souza Pinto, 2001)
U (%)
T
U (%)
T
U (%)
T
U (%)
T
U (%)
T
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
0,0001
0,0003
0,0007
0,0013
0,0020
0,0028
0,0038
0,0050
0,0064
0,0078
0,0095
0,0113
0,0133
0,0154
0,0177
0,0201
0,0277
0,0254
0,0283
0,0314
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
0,0346
0,0380
0,0415
0,0452
0,0491
0,0531
0,0572
0,0616
0,0660
0,0707
0,0755
0,0804
0,0855
0,0908
0,0962
0,102
0,108
0,113
0,119
0,126
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
0,132
0,138
0,145
0,152
0,159
0,166
0,173
0,181
0,189
0,197
0,204
0,212
0,221
0,230
0,239
0,248
0,257
0,266
0,276
0,287
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
0,297
0,307
0,318
0,329
0,340
0,351
0,364
0,377
0,389
0,403
0,416
0,431
0,445
0,461
0,477
0,493
0,510
0,528
0,547
0,567
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
0,588
0,610
0,633
0,658
0,684
0,712
0,742
0,774
0,809
0,848
0,891
0,938
0,992
1,054
1,128
1,219
1,335
1,500
1,781
∞
101
4.9.
REFORÇO USADOS COMO COMPONENTES PARA O CONTROLE DA
ESTABILIDADE E RECALQUE DO ATERRO
Existem várias técnicas para aumentar a força de cisalhamento efetiva da
fundação em solos moles e controlar sua consolidação pós construção.
Estas técnicas incluem drenagem, grouting, estaqueamento e a completa
substituição do solo. A técnica de estaqueamento permite a construção de aterros
de qualquer altura, com qualquer velocidade construção (assumindo que o aterro é
estável) com subseqüente controle de recalques pós construção. Reforços na base
podem ser usados como “pontes” (promovendo o arqueamento do solo) entre os
capteis das estacas para distribuir as cargas entre os mesmos e aumentar os
benefícios econômicos das estacas instaladas como fundação sobre solos moles
(ver figura 59).
Muitos tipos de estacas podem ser utilizadas em aterros, incluindo estacas
cravadas ou moldadas “in loco” de concreto, estacas de madeira, colunas de brita ou
concreto, injeção de grout, colunas de cimento ou areia compactada.
Normalmente se adota que toda a carga do aterro será transferida através das
estacas para uma camada de solo resistente. Consequentemente, a performance do
aterro e as características do solo mole de fundação, têm que ser consideradas
somente com relação ao tipo de estacas usadas e sua instalação.
Reforços de base instalados entre os capteis das estacas podem ser usadas
para transferir a carga do aterro para os pilares. O reforço permite um aumento no
espaçamento entre as estacas e uma redução no tamanho dos capteis.
Adicionalmente o reforço absorve os esforços horizontais do aterro eliminando a
necessidade da utilização das estacas de equilíbrio ao longo dos limites da
fundação, ver figura 45.
Formatado: Nível 2
102
Figura 45 - Configurações de aterros estaqueados.
Fonte : (Maccaferri, adaptado de BS8006 ).
A máxima carga de tração no estado limite último Tr por metro linear na base
de aterros reforçados deve ser a seguinte:
- Na direção longitudinal do aterro a máxima carga deve ser aquela necessária
para transferir o carregamento vertical do aterro sobre os capitéis das estacas
Trp;
- Na direção transversal do aterro a máxima carga deve ser a soma da carga
necessária para transferir o carregamento vertical do aterro para os capteis das
estacas Trp com a carga necessária para resistir ao deslizamento lateral Tds.
103
Para assegurar que o estado limite último que governa a ruptura do reforço
não será atingido durante a vida útil de projeto do reforço, a seguinte condição deve
ser verificada:
TD
≥ Tr
fn
(41)
Onde:
TD = é a resistência de projeto para o reforço;
fn = é o fator parcial que rege as ramificações econômicas de uma possivel
falha, ver a tabela 9.
Para assegurar que a carga que gera a condição de limite ultimo pode ser
desenvolvida no reforço, é necessário que exista uma adequada adesão entre o
mesmo e o solo adjacente.
Para cada esforço limite a ser determinado, uma adesão associada ao reforço
também deve ser verificada, para garantir que a carga que gera a condição de limite
ultimo pode ser gerada no reforço.
104
Figura 46 - Estado limite ultimo para aterros estaqueados com base reforçada.
Fonte : (Maccaferri, adaptado de BS8006 ).
4.9.2. CAPACIDADE DE UM GRUPO DE ESTACAS
Formatado: Nível 3
Por razões de economia, a distância entre estacas adjacentes deve ser
maximizada. Se as estacas forem instaladas em uma malha quadrada, o
espaçamento máximo entre elas “s” será:
s=
(f
Qp
fs
.γ .H + f q .ω s )
(42)
105
Onde:
=
é a capacidade de carga admissível de cada estaca que forma o
=
é o fator parcial de segurança para o peso específico do solo,
γ
=
é o peso específico do material que forma o aterro;
H
=
é a altura do aterro;
fq
=
é o fator de segurança parcial para as cargas externas
Qp
grupo;
ffs
ver tabela 9;
aplicadas, ver tabela 9;
ωs
=
é a sobrecarga externa.
Figura 47 - Estado limite de servicibilidade (utilização) para aterros estaqueados com
reforço de base.
Fonte : ( Maccaferri, adaptado de BS8006 ).
106
4.9.3. GRUPO DE ESTACAS EXTENDIDO
Formatado: Nível 3
A área estaqueada deverá ser extendida a uma distância além do limite da
crista do aterro, para garantir que qualquer recalque diferencial ou instabilidade fora
da área estaqueada, não afetará a estabilidade do talude formado pelo mesmo (ver
figura 47b). O limite externo para posicionamento dos capitéis das estacas externas
do grupo é dado por :
L p = H .(n − tan θ p )
(43)
Onde:
Lp
=
é a distância horizontal entre o limite externo dos capitéis das
estacas externas do grupo e o pé do talude do aterro, ver figura 48;
é a altura do aterro;
H
=
n=
é a inclinação do talude do aterro na forma n-horizontal/1vertical;
γ=
é o peso específico do material que forma o aterro;
θp
=
é o ângulo, apartir da vertical, entre o limite externo dos capitéis
das estacas externas do grupo e a crista do talude do aterro, ver figura 48;
O material de aterro é caracterizado por φ’cv sendo:
ϕ p = 45o −
ϕ cv'
2
(44)
107
Figura 48 - Limite dos capteis.
Fonte : (Maccaferri, adaptado de BS8006 ).
4.9.4. DISTRIBUIÇÃO DAS CARGAS VERTICAIS
Formatado: Nível 3
É necessário que as cargas verticais do aterro sejam transferidas para os
capitéis das estacas.
Para assegurar que não ocorrerão recalques diferenciais localizados na
superfície do aterro (que pode ser um problema para aterros baixos), recomenda-se
que a relação entre a altura do aterro e o espaçamento entre capitéis seja:
H ≥ 0,70.(s − a )
(45)
Onde:
a=
é o tamanho do capitel (considerando que a capacidade de carga total
da estaca pode ser mobilizada nas bordas do capitel);
é a altura do aterro;
H
=
s=
é o espaçamento entre estacas adjacentes.
Devido às significantes diferenças entre as deformações características que
existem entre as estacas e o solo mole que a cerca, a distribuiçào de pressões
verticais na base do aterro é não uniforme. O arqueamento do solo entre os capitéis
de estacas adjacentes induz a grandes pressões verticais sobre as estacas e
108
consequentemente menores cargas sobre o solo circundante. A razão entre a
pressão vertical exercida no topo dos capitéis das estacas e a pressão vertical
média na base do aterro (P’c/σ’v) pode ser estimada através do uso da fórmula de
Marston para projetos de tubos subsuperficiais, .
C a 
= c 
'
σv  H 
pc'
2
(46)
Onde:
p’c
σ’v
=
=
é a pressão vertival aplicada nos capitéis das estacas;
é igual a ( f fs .γ .H + f q .ω s ) que é a pressão vertical média do
aterro na base fatorada;
γ
=
é o peso específico do material que forma o aterro;
H
=
é a altura do aterro;
ωs
=
é a sobrecarga externa uniformemente distribuída;
Cc
=
é o coeficiente de arqueamento;
a
=
é o tamanho (ou diâmetro) dos capitéis das estacas.
Valores para o coeficiente de arqueamento Cc são mostrados na tabela 15.
Tabela 15 – Coeficiente de arqueamento Cc para reforço de aterros estaqueados
Fonte: ( BS 8006 )
Tipo de estaca
Coeficiente de arqueamento
Com resistência de ponta (não flexível)
C c = 1,95. H a − 0,18
Por atrito e outros tipos (normal)
C c = 1,50. H a − 0,07
A carga distribuída (WT) transportada pelo reforço entre os capitéis de estacas
adjacentes pode ser determinada por:
Para H > 1,40.( s − a ) ;
WT =
1,40.s. f fs .γ .( s − a )
s2 − a2
[
⋅ s 2 − a 2 .( p c' σ v' )
]
(47)
109
Para 0,70.( s − a ) ≤ H ≤ 1,40.( s − a )
WT =
s.( f fs .γ .H + f qω s )
s2 − a2
[
⋅ s 2 − a 2 .( p c' σ v' )
Porém WT = 0 se s / a ≤ pc
2
2
'
]
(48)
σ v' ;
Onde:
WT
=
é a carga vertical distribuída atuando no reforço entre os capitéis
de estacas adjacentes, ver figura 49;
ffs
=
é o fator parcial de segurança para o peso específico do solo,
=
é o fator de segurança parcial para as cargas externas
ver tabela 9;
fq
aplicadas, ver tabela 9;
ωs
=
é a sobrecarga externa.
Para um reforço extensível a carga de traçào Trp por metro gerada no reforço
como resultado da carga distribuída WT será :
Trp =
WT .(s − a)
⋅ 1+ 1
6.ε
2.a
(49)
Onde:
Trp
=
é a carga de tração no reforço, ver figura 49;
ε
=
é a deformação do reforço.
A equação acima tem duas incógnitas Trp e ε. É solucionada para Trp tomandose em conta a deformação máxima admissível para o reforço e através do
conhecimento das características tensão/deformação do reforço a diferentes niveis
de carga.
A carga de tração Trp se desenvolve à medida que o reforço se deforma sob a
ação do peso do aterro. Isto normalmente ocorre durante a construção do aterro
mas, em situações nas quais o reforço não pode deformar durante a construção, o
110
reforço não será solicitado pelas cargas aplicadas até que haja a deformação ou
assentamento da fundação.
A equação acima para Trp é apropriada para aqueles reforços que podem
sofrer deformações durante o carregamento, tais como os reforços extensíveis (ex.
poliméricos). Para reforços inestensíveis (ex. barras metálicas) relações alternativas
poderão ser usadas para determinar a sua resistência à tração máxima admissível.
Figura 49 - Variáveis usadas na determinação de Trp.
Fonte : (Maccaferri, adaptado de BS8006 ).
111
4.9.5. ESCORREGAMENTO LATERAL
Formatado: Nível 3
O reforço deverá resistir também aos esforços horizontais gerados pelo
escorregamento lateral, ver figura 46d. Esta carga de tração no reforço deverá ser
gerada a uma deformação compatível com os movimentos laterais admissíveis para
as estacas, eliminando assim a necessidade de estacas de travamento. A carga de
tração no reforço Tds necessária para resistir ao empuxo solicitante (para fora)
gerado pelo aterro será (de acordo com a figura 50):
Tds = 0,50.K a .( f fs .γ .H + 2. f q .ω s ).H
(50)
Onde:
Tds
=
é a carga de tração no reforço por metro, necessária para resistir
ao empuxo lateral gerado pelo aterro;
Ka
=
é o coeficiente de empuxo ativo [ = 45 o − ϕ cv 2 ];
H
=
é a altura do aterro;
γ
=
é o peso específico do material que forma o aterro;
ωs
=
é a intensidade da sobrecarga externa no topo do talude;
ffs
=
é o fator parcial de segurança para o peso específico do solo,
=
é o fator de segurança parcial para as cargas externas
ver tabela 9;
fq
aplicadas, ver tabela 9.
Para gerar a carga de tração Tds no reforço, o aterro não deve deslizar sobre o
mesmo (ver figura ). Para evitar este deslizamento horizontal, o mínimo comprimento
de ancoragem Le deve ser:
Le ≥
0,50.K a .H .( f fs .γ .H + 2. f q .ω s ). f s . f n
γ .h.
α ' . tan ϕ cv'
f ms
(51)
Onde:
fs =
é o fator de segurança parcial para a resistência ao deslizamento do
reforço, ver tabela 9;
112
fn
=
é o fator de segurança parcial que governa as ramificações
econômicas do mecanismo de falha, ver tabela 9;
h
=
é a altura média do aterro sobre o reforço ao longo do
comprimento Le;
α’
=
é o coeficiente de interação solo/ângulo de adesão do reforço
=
é o ângulo de atrito do aterro a grandes deformações sob
tang φ’cv;
φ’cv
condições de tensões efetivas;
fms
=
é o fator parcial de segurança para o material aplicado ao valor
tang φ’cv, ver tabela 9;
Figura 50 - Estabilidade lateral contra o deslizamento na interface aterro / reforço.
Fonte : (Maccaferri, adaptado de BS8006).
Formatado: Título 3
4.9.6. ANCORAGEM DO REFORÇO
O reforço deverá atingir uma adequada ancoragem com o solo adjacente nas
extremidades da área estaqueada. Isto é necessário para garantir que as máximas
tensões do estado limite poderão ser geradas (no sentido transversal e ao longo do
comprimento do aterrro) entre as duas filas externas de estacas. No sentido
transversal (através da largura do aterro) o reforço deverá se extender a uma
distancia mínima além da linha mais externa de estacas, tal distancia é dada por:
113
(T
Lb ≥
rp
+ Tds ). f n . f p
 α '1. tan ϕ cv' 1
γ .h.
f ms

+
α ' 2 . tan ϕ cv' 2 
f ms



(52)
Onde:
Lb
=
é o comprimento de ancoragem necessário, além da linha de
estacas mais externa, no sentido transversal, ver figura 50
fp
=
é o fator de segurança parcial aplicado à resistência do reforço
ao pull-out (arrancamento), ver tabela;
fn
=
é o fator de segurança parcial que governa as ramificações
econômicas do mecanismo de falha, ver tabela 9;
Tds
=
é a carga de tração no reforço por metro, necessária para resistir
ao empuxo lateral gerado pelo aterro, calculada de acordo com o item 4.9.5;
Trp
=
é a carga de tração no reforço;
h
=
é a altura média do aterro sobre o reforço ao longo do
comprimento Le;
γ
=
é o peso específico do material que forma o aterro;
α’1
=
é o coeficiente de interação solo/ângulo de adesão do reforço
tang φ’cv1, em um lado do reforço;
α’2
=
é o coeficiente de interação solo/ângulo de adesão do reforço
tang φ’cv2, no lado oposto do reforço;
fms
=
é o fator parcial de segurança para o material aplicado ao valor
tang φ’cv, ver tabela 9;
Ao longo do comprimento o reforço deverá extender-se uma distancia mínima
além da linha mais externa de estacas, tal distancia é dada por:
Lb ≥
Trp . f n . f p
 α . tan ϕ cv' 1 α ' 2 . tan ϕ cv' 2 

+
γ .h.

f
f
ms
ms


'
1
(53)
114
4.9.7. ESTABILIDADE GLOBAL
Formatado: Nível 3
A estabilidade global da estrutura de aterro estaqueado deve ser analizada por
métodos de estabilidade convencionais, com as modificações necessárias para
tomar em conta a presença da fundação estaqueada e o reforço a plicado na base
do aterro, ver figura 51. As análises podem ser realizadas usando-se parâmetros em
termos de tensões efetivas tomando em consideração as poro-pressões geradas
pela água, ver figura 51, porém uma análise de estabilidade a curto prazo deveria
assumir condições não drenadas.
Para assegurar estabilidade a seguinte condiçào deve ser satisfeita em
qualquer local ao longo da base do aterro:
M D ≤ M RS + M RP + M RR
(54)
Onde:
MD
=
é o momento solicitante em todos os pontos ao longo da base do
aterro, ver figura 51;
MRS
=
é o momento resistente devido ao solo em todos os pontos ao
longo da base do aterro, ver figura 51;
MRP
=
é o momento resistente devido às estacas em todos os pontos
ao longo da base do aterro, ver figura 51;
MRR
=
é o momento resistente devido ao reforço em todos os pontos ao
longo da base do aterro, ver figura 51
115
Figura 51 - Variáveis utilizadas na analise de estabilidade global em aterros
estaqueados com reforço de base.
Fonte : (Maccaferri, adaptado de BS8006 ).
4.9.8.
DEFORMAÇÃO NO REFORÇO
A máxima deformação aceitável no reforço εmáx deverá ser limitada para evitar
que ocorra recalques diferenciais na superfície do aterro.
A deformação de tração inicial no reforço é necessária para mobilizar o esforço
de tração. Como prática, pode ser imposta uma deformação máxima de até 6% para
assegurar que todos os carregamentos provenientes do aterro sejam transferidos
para as estacas. Para aterros de pequena espessura (ou de pequena altura) esta
máxima deformação deverá ser reduzida para evitar recalques diferenciais na
superfície do aterro.
A deformação a longo prazo do reforço (devido à fluência) deverá ser mantida
em um mínimo para assegurar que ao longo da vida útil da obra recalques
localizados não ocorram na superfície do aterro. A máxima deformação aceitável por
fluência no reforço é de 2% acima daquela prevista em projeto.
Formatado: Nível 3
116
5.
CONCLUSÃO
Através desta pesquisa, conclui-se que a estabilidade de um aterro construído
sobre solo mole é governada principalmente pela resistência ao cisalhamento da
fundação, e a construção de um aterro sobre solo mole é um problema de
capacidade de carga. O reforço deve ser colocado ao nível da fundação (base) para
prever falhas por cisalhamento em ambos elementos, no aterro e no solo de
fundação, qualquer redução no recalque diferencial é de importância secundária.
Uma importante consideração é aquela na qual estabilidade do aterro é mais
crítica durante a sua construção. Isto se deve à relativa baixa permeabilidade do
solo mole que não permite a completa consolidação durante o período de
construção. Ao final da construção a carga do aterro foi totalmente aplicada, mas o
ganho da resistência ao cisalhamento do solo de fundação devido à consolidação
pode ser insuficiente para garantir a estabilidade.
Uma vez ocorrida a consolidação, a melhoria resultante da resistência ao
cisalhamento do solo da fundação irá remover a necessidade do uso de reforços
para melhorar a estabilidade. Deste modo durante o período entre o final da
construção e a consolidação da fundação o requerimento fundamental de resistência
do reforço é aquele de garantir, em qualquer instante neste intervalo, que a
resistência de projeto se iguale ou supere a carga de projeto.
O reforço da base estabiliza um aterro sobre solo mole através da prevenção
da ruptura lateral do aterro, da extrusão (ruptura) do solo de fundação e da ruptura
global. Esta força estabilizante é gerada no reforço através da tensão de
cisalhamento transmitida do solo de fundação e do aterro que colocam o reforço em
tensão.
Porém, as outras etapas que foram descritas no início deste trabalho, são de
suma importância para um projeto de aterro reforçado sobre solo mole com
geogrelhas, desde a elaboração de especificação, memorial e desenhos, que é a
etapa onde se apresentará geometricamente os resultados das metodologias,
apresentadas neste trabalho, até as etapas acompanhamento da execução da obra
e Avaliação do desempenho, sendo estas onde aplicará em campo estas
metodologias.
Em alguns casos de obras de engenharia, principalmente aquelas de grande
porte, ou que envolva algum nível maior de risco que possa comprometer não só
Formatado: Nível 1
117
perdas materiais significativas, mas também risco de perda de vidas humanas, há a
necessidade de se acompanhar a evolução do seu comportamento após a sua
conclusão. Assim, nestes casos são montados instrumentos apropriados para o
acompanhamento, com leituras, das informações mais relevantes no que se refere
ao seu comportamento.
Enfim, acredita-se que este trabalho contribuirá aos profissionais da área e
graduantes para a aquisição de conhecimentos sobre as metodologias necessárias
para a elaboração de Projetos de Aterros Reforçados sobre solos moles.
118
6.
REFERÊNCIAS BIBIOGRÁFICAS
ABRAMENTO, M., KOSHIMA, A., ZIRLIS, A. C., Reforço do Terreno, In:
ABMS/ABEF (eds), Fundações – Teoria e Prática, 2 ed., capítulo 18, São Paulo, Ed.
PINI. 1998.
BARROS, C.L. A, Apostila de ensaios de laboratoriais de geotecnia – 1997.
BRITISH STANDARD - Code of practice for “Strengthened / Reinforced soils and
others fills”, BS 8006:1995.
MASSAD, F., 2003 - Obras de Terra “Curso básico de geotecnia”, São Paulo: Oficina
de Textos.
MANUAL MACCAFERRI SIMPIFICADO PARA APLICAÇÕES EM
GEOSSINTÉTICOS. Departamento Técnico, Jundiai. 2009
NOGUEIRA, J.B., Apostila de mecânica dos solos – Ensaios de Laboratório, EESC
USP – 1971.
ORTIGÃO, J. A., Introdução à mecânica dos solos dos estados críticos, Rio de
Janeiro, Livros técnicos e Científicos Editora Ltda., 1993.
PACHECO SILVA, F. Uma nova construção gráfica para a determinação da pressão
de pré-adensamento de uma amostra de solo. COBRAMSEF, Rio de Janeiro, Vols. I
e II, Tomo I, pp. 219-224, 1970.
SCHNAID, F. Ensaios de campo e suas aplicações à engenharia de fundações. São
Paulo; Oficina de Textos. 189p. 2000.
SANTOS, P. – Manual Maccaferri de reforço de Solo. 1 ed. Vol 1 Jundiai. 2008
SOUSA PINTO, C. – Curso básico de mecânica dos solos, em 16 aulas. 1 ed. São
Paulo – Oficina de Textos, 2001.
Formatado: Nível 1
119
TEIXEIRA, S. H. C., Estudo da Interação solo-geogrelha em testes de arrancamento
e a sua aplicação na análise e dimensionamento de maciços reforçados. São Carlos,
2003. 214p. Tese de Doutorado submetida à Escola de Engenharia de São Carlos –
Universidade de São Paulo, 2003.
TERZAGHI, K. and PECK, R.B., Soil Mechanics in Engineering Practice, 2nd ed.,
McGraw Hill, New York, NY, USA, 1987.
VARGAS, M., - Introdução à Mecânica dos Solos, McGraw-Hill do Brasil Ltda, 1979.
VERTEMATTI, J. C. Manual Brasileiro de Geossintéticos. Editora Edgard Blücher
LTDA, ABINT, São Paulo, 2004
http://www.abeg.com.br
http://www.insitu.com.br