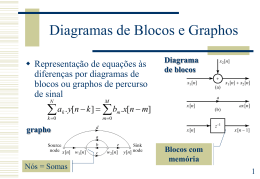
4.4 Secções planas de
superfícies e sólidos
Geometria Descritiva
2006/2007
Cidália Fonte – Faculdade de Ciências e Tecnologia da Universidade de Coimbra
Secções planas de superfícies e
sólidos

Quando um plano intersecta uma superfície
geométrica determina sobre ela uma linha plana
que pertence à superfície

A linha obtida pode ser



uma circunferência
rectas (problema mais simples)
A linha pode ser uma curva complexa


Ela terá que ser identificada ponto a ponto
É útil conhecer a tangente à secção plana em cada ponto

A tangente à secção plana é a recta de intersecção do plano
secante que gera a secção plana com o plano tangente à curva
nesse ponto
Cidália Fonte – Faculdade de Ciências e Tecnologia da Universidade de Coimbra
Secções planas de poliedros


Aplicação a prismas pirâmides e outros poliedros
1º caso: O plano secante é projectante


A secção fica determinada pela intersecção de cada
aresta do sólido com o plano secante projectante
2º caso: O plano secante não é projectante

A secção é obtida através da intersecção do plano que
contém cada face do sólido com o plano secante
Cidália Fonte – Faculdade de Ciências e Tecnologia da Universidade de Coimbra
Secções planas de poliedros

Aplicação a prismas pirâmides e poliedros
Determinar a secção
plana definida pelo plano
de frente 1 com o prisma
hexagonal regular com
bases de nível
 A secção é o rectângulo
MNN’M’
M’2

M2
N2
X
M1 M’1
(h1)
Cidália Fonte – Faculdade de Ciências e Tecnologia da Universidade de Coimbra
N’2
N1 N’1
Secções planas de poliedros

Aplicação a prismas pirâmides e poliedros
Determinar a secção plana
definida pelo plano vertical  com
uma pirâmide pentagonal regular
assente em 0
 A secção é o polígono MNPQR
Para se obter a secção em
verdadeira grandeza fez-se o seu
rebatimento sobre o plano
horizontal

M2
R2
N2
Q2
X
R1
h
P1
Q1M1
N1
Pr1
Qr1
Rr1
Cidália Fonte – Faculdade de Ciências e Tecnologia da Universidade de Coimbra
f
P2
Nr1
Mr1
Secções planas de superfícies
cónicas e cilíndricas

1º caso: O plano secante passa pelo vértice da
superfície

O plano intersecta a directriz

Num ponto:


Em vários pontos:


A secção plana é a geratriz da superfície que passa nesse
ponto
A secção plana é constituída por geratrizes
O plano não intersecta a directriz

A secção plana reduz-se a um ponto (o vértice da superfície)
Cidália Fonte – Faculdade de Ciências e Tecnologia da Universidade de Coimbra
Secções planas de superfícies
cónicas e cilíndricas



A superfície é definida pelo vértice V e pela directriz d
(num plano  de topo)
O plano secante é definido pelas rectas r e s concorrentes
em V (portanto o plano contém o vértice da superfície)
Determinar a secção definida na superfície pelo plano
secante
s
Identificam-se
as geratrizes que
definem a secção plana identificando
dois dos seus pontos pertencentes à
directriz (pontos A e B)
O
plano secante intersecta o plano que
contém a directriz segundo a recta i, que
determina sobre a directriz os pontos A e B
 A secção plana é constituída pelas geratrizes
g e g’
2
V2
A2
(f)di2
g’2
g2
r2
2
X
s1
V1
r1
A1
i1
Cidália Fonte – Faculdade de Ciências e Tecnologia da Universidade de Coimbra
B2
g1
B1
g’1
d1
Secções planas de superfícies
cónicas e cilíndricas

2º caso: O plano secante não passa pelo
vértice da superfície


A secção não contém nenhuma geratriz
A secção é constituída pelos pontos de intersecção
de cada uma das geratrizes com o plano secante
Cidália Fonte – Faculdade de Ciências e Tecnologia da Universidade de Coimbra
Secções planas de superfícies
cónicas e cilíndricas de revolução

As secções planas de superfícies cónicas ou
cilíndricas de revolução são cónicas:

Elipses
Parábolas
Hipérboles

Considerando que







uma circunferência é o caso particular de uma elipse
um ponto é um caso particular de uma circunferência
duas rectas paralelas são uma parábola degenerada
duas rectas coincidentes são uma parábola degenerada
duas rectas concorrentes são uma hipérbole degenerada
Cidália Fonte – Faculdade de Ciências e Tecnologia da Universidade de Coimbra
Secções planas de superfícies
cónicas e cilíndricas de revolução

2º caso: O plano secante não passa pelo
vértice da superfície



Se o plano secante intersecta todas as
geratrizes da superfície a cónica é uma elipse
(curva fechada)
Se o plano secante é paralelo apenas a uma
das geratrizes a cónica é uma parábola
Se o plano secante é paralelo apenas a duas
geratrizes a cónica é uma hipérbole
Cidália Fonte – Faculdade de Ciências e Tecnologia da Universidade de Coimbra
Secções planas de superfícies
cónicas e cilíndricas de revolução
Parábola
Círculo
Hipérbole
Elipse
Cidália Fonte – Faculdade de Ciências e Tecnologia da Universidade de Coimbra
Secções planas de superfícies
cónicas e cilíndricas de revolução

Note-se que:

A secção plana de uma superfície cilíndrica nunca
pode ser uma parábola ou uma hipérbole


O plano secante não pode ser paralelo a uma ou a duas
geratrizes sem ser paralelo a todas
Para determinar se a secção plana de uma
superfície cónica é uma elipse, uma parábola ou
uma hipérbole faz-se passar pelo vértice um
plano  paralelo ao plano secante 

O plano  determina quais são as geratrizes
paralelas a 
Cidália Fonte – Faculdade de Ciências e Tecnologia da Universidade de Coimbra
Secções planas de superfícies
cónicas e cilíndricas de revolução

Determinar que tipo de superfície é a secção plana
definida pelo plano  na porção de superfície cónica
de revolução indicada
A
2
Considera-se uma recta r, de frente,
paralela ao plano  e que passa no vértice
 Considera-se o plano  paralelo a  e que
contém r
 Este plano intersecta a superfície segundo
duas geratrizes AVA’ e BVB’ que são
portanto paralelas a 
 A secção plana é portanto uma hipérbole

B’2
r2
V2
B2
A’2
f
B1
A1
X
r1
V1
Nota: Se a directriz da superfície cónica não estivesse sobre o plano frontal de
projecção teríamos que o colocar nessa posição fazendo uma mudança do
plano frontal de projecção ou determinando nova directriz sobre este plano
Cidália Fonte – Faculdade de Ciências e Tecnologia da Universidade de Coimbra
f
h
B’1
A’1
h
Secções planas de superfícies
cónicas e cilíndricas de revolução

Determinar a secção plana definida pelo plano
de topo  no cone indicado
Cr Dr
Br
1
1
1
plano de topo  intersecta todas
as geratrizes do cone, logo a secção
plana é uma elipse
O
Ar1
A
projecção cilíndrica de uma elipse é
sempre uma elipse
(f)
Er1
Fr1
Gr
Hr1 1
D F
H2 2 E2
B
2
A2
2
C2G2
Circunferência
(caso particular de uma elipse)
Segmento rectilíneo (elipse degenerada)
Determinam-se
os pontos de intersecção
do plano com as geratrizes
A
elipse resultante é ABCDEFGH
Para
que apareça em verdadeira
grandeza fez-se o seu rebatimento
Cidália Fonte – Faculdade de Ciências e Tecnologia da Universidade de Coimbra
X
H1
A1
G1
F1
E1
B1 C1 D1
Secções planas de superfícies
cónicas e cilíndricas de revolução

Determinar a secção plana definida pelo
plano  no cone indicado
f
plano  não é projectante
Faz-se uma mudança do plano frontal de
projecção de forma a transformá-lo num
plano de topo
O plano  intersecta todas as geratrizes do
cone, logo a secção plana é uma elipse
Determinam-se os pontos de intersecção do
plano com as geratrizes
A elipse resultante é ABCDEFGH
Para que as elipses apareçam em
verdadeira grandeza será necessário fazer o
seu rebatimento
1
O
P21
P2
f
X
P1
hh1
Cidália Fonte – Faculdade de Ciências e Tecnologia da Universidade de Coimbra
Secções planas de superfícies
cónicas e cilíndricas de revolução

Determinar a secção plana definida pelo
plano  no cone indicado
f
plano  não é projectante
Faz-se uma mudança do plano frontal de
projecção de forma a transformá-lo num
plano de topo
O plano  intersecta todas as geratrizes do
cone, logo a secção plana é uma elipse
Determinam-se os pontos de intersecção do
plano com as geratrizes
A elipse resultante é ABCDEFGH
Para que as elipses apareçam em
verdadeira grandeza será necessário fazer o
seu rebatimento
1
A21 B H
21
21
C21G21
D21 F21
O
E21
f
X
H G1
A1 1 F1
B1
E1
C1
D1
hh1
Cidália Fonte – Faculdade de Ciências e Tecnologia da Universidade de Coimbra
Secções planas de superfícies
cónicas e cilíndricas de revolução

Determinar a secção plana definida pelo
plano  no cone indicado
f
plano  não é projectante
Faz-se uma mudança do plano frontal de
projecção de forma a transformá-lo num
plano de topo
O plano  intersecta todas as geratrizes do
cone, logo a secção plana é uma elipse
Determinam-se os pontos de intersecção do
plano com as geratrizes
A elipse resultante é ABCDEFGH
Para que as elipses apareçam em
verdadeira grandeza será necessário fazer o
seu rebatimento
1
A21 B H
21
21
C21G21
D21 F21
O
E21
A2
B2 H2G2F
2
C2
D2 E2
f
X
H G1
A1 1 F1
B1
E1
C1
D1
hh1
Cidália Fonte – Faculdade de Ciências e Tecnologia da Universidade de Coimbra
Secções planas de superfícies
cónicas e cilíndricas de revolução

Determinar a secção plana definida pelo
plano  no cone indicado
plano  não é projectante
Faz-se uma mudança do plano frontal de
projecção de forma a transformá-lo num
plano de topo
O plano  intersecta todas as geratrizes do
cone, logo a secção plana é uma elipse
Determinam-se os pontos de intersecção do
plano com as geratrizes
A elipse resultante é ABCDEFGH
Para que as elipses apareçam em
verdadeira grandeza será necessário fazer o
seu rebatimento
O
A2
B2 H2G2F
2
C2
D2 E2
f
X
H G1
A1 1 F1
B1
E1
C1
D1
hh1
Cidália Fonte – Faculdade de Ciências e Tecnologia da Universidade de Coimbra
Secções planas de superfícies
cónicas e cilíndricas de revolução

Determinar a secção plana definida pelo
f f
plano  no cone indicado

plano  não é projectante
Faz-se uma mudança do plano horizontal de
projecção de forma a transformar  num
plano vertical
O plano  é paralelo apenas a uma geratriz
do cone (que passa no vértice e no ponto A),
logo a secção plana é uma parábola
Determina-se as suas projecções através
das projecções dos pontos de intersecção do
plano com as geratrizes
1
A2
O
X
P2
A11
P1
h
P11
h1
Cidália Fonte – Faculdade de Ciências e Tecnologia da Universidade de Coimbra
Secções planas de superfícies
cónicas e cilíndricas de revolução

Determinar a secção plana definida pelo
plano de topo  no duplo cone indicado
o plano  paralelo a  e que
passa pelo vértice do duplo cone
O plano  intersecta o cone segundo duas
geratrizes AVA’ e BVB’ que são paralelas a 
Logo a secção plana definida pelo plano  é
uma hipérbole
Os pontos M e N são os vértices da hipérbole
e C é o ponto médio do eixo transverso MN da
hipérbole
A2 B2 f
Considera-se
plano frontal  é um plano de simetria da
hipérbole, logo o eixo transverso é frontal
f
M2
V2
C2
N2
X
A’2B’2
A1
B’
1
O
Para
que a hipérbole apareça em verdadeira
grandeza é necessário fazer o seu rebatimento
Cidália Fonte – Faculdade de Ciências e Tecnologia da Universidade de Coimbra
h
V1
B1
C1
h A’1 h
Secções planas de superfícies de
revolução

1º caso: O plano secante contém o eixo da
superfície


2º caso: O plano secante é perpendicular ao eixo
da superfície


A secção plana é uma meridiana da superfície
A secção plana é um paralelo da superfície
3º caso: O plano secante é oblíquo ao eixo da
superfície


A secção plana é determinada por pontos que podem ser
determinados sobre cada paralelo ou sobre cada meridiana
Determina-se a recta de intersecção do plano secante com o plano
do paralelo ou da meridiana e consideram-se os pontos comuns à
recta obtida e ao paralelo ou à meridiana
Cidália Fonte – Faculdade de Ciências e Tecnologia da Universidade de Coimbra
Secções planas de uma esfera

A secção plana de uma esfera é sempre um
círculo


O centro do círculo é o pé da perpendicular baixada do
centro da esfera para o plano secante
As projecções do círculo são elipses


O eixo maior é a projecção do diâmetro paralelo ao plano de
projecção respectivo (projecta-se em verdadeira grandeza)
O eixo menor é a projecção do diâmetro perpendicular ao
diâmetro paralelo ao plano de projecção em questão.
Cidália Fonte – Faculdade de Ciências e Tecnologia da Universidade de Coimbra
Secções planas de uma esfera

Determinar a secção plana definida pelo
plano de topo  na esfera representada
O
centro do círculo correspondente à
secção plana é o ponto C
A projecção frontal da secção reduz-se ao
segmento de recta A2B2
A projecção horizontal é a elipse com
 centro em C1,
 eixo maior E1D1=A2B2
 eixo menor A1B1
(f)
(f)
(f)
X
B2
F2G2
C2D2E2
I2 J2
O2
A2
G1
E1
J1
A1
B1 O C1
1
F1
Cidália Fonte – Faculdade de Ciências e Tecnologia da Universidade de Coimbra
D1
I1
4.5 Intersecção de rectas com
sólidos
Geometria Descritiva
2006/2007
Cidália Fonte – Faculdade de Ciências e Tecnologia da Universidade de Coimbra
Intersecção de rectas com sólidos


Faz-se passar pela recta um plano auxiliar
que intersectará o sólido segundo uma
secção plana
Os pontos comuns à recta e à secção
plana são os pontos procurados
Cidália Fonte – Faculdade de Ciências e Tecnologia da Universidade de Coimbra
Intersecção de rectas com sólidos

Determinar a intersecção de um octaedro regular com 3 cm
de aresta e uma diagonal vertical, tendo o ponto de menor
cota a cota zero, com a recta r
Considera-se o plano de topo  que
contém a recta r
 Determina-se a secção plana definida no
octaedro pelo plano 
 A secção obtida é um polígono com
vértices A, B, C, D, E e F
 Determinam-se os pontos de intersecção
da secção plana com a recta r (pontos R e
S)
 Para obter a secção em verdadeira
grandeza pode rebater-se o plano 

R2 A2 B2
C2 F2
D2 E2S2
r2 (f)
X
C1
B1
R1 V
S1
1
A1
F1
Cidália Fonte – Faculdade de Ciências e Tecnologia da Universidade de Coimbra
D1
E1
r1
Intersecção de uma recta com
superfícies cónicas e cilíndricas

Faz-se passar pela recta um plano auxiliar
que intersectará a superfície segundo
uma secção plana


Por exemplo o plano que passa pelo vértice
Os pontos comuns à recta e à secção
plana são os pontos procurados
Cidália Fonte – Faculdade de Ciências e Tecnologia da Universidade de Coimbra
Intersecção de uma recta com
superfícies cónicas e cilíndricas

Determinar a intersecção da recta s com a superfície
Q
cilíndrica definida pela directriz
d (situada num plano de topo) e
pela direcção das geratrizes r r
s
2
2
o plano auxiliar definido
pela recta s e pela direcção das
geratrizes
A intersecção deste plano com o plano
 que contém a directriz é a recta i
A intersecção da recta i com a directriz
define os pontos A e B
Por A e B passam as geratrizes g e g’
que constituem a secção plana
A intersecção da recta s com a secção
plana (são complanares) definem os
pontos procurados P e Q
2
Considera-se
Q1
P2
r’2
g2
g’2
A2
X
B1
g1
r’1
Cidália Fonte – Faculdade de Ciências e Tecnologia da Universidade de Coimbra
(f)d2i2
g’1
P1
r1
B2
i1
A1
s1
d1
Intersecção de uma recta com
uma esfera



Utiliza-se um plano auxiliar
projectante que contém a recta
Determina-se a secção plana
formada na esfera pelo plano
auxiliar
Determina-se a intersecção da
secção plana com a recta

Para se obter a posição dos pontos
com maior precisão pode rebater-se a
secção plana e a recta em torno por
exemplo de uma recta frontal f
Cidália Fonte – Faculdade de Ciências e Tecnologia da Universidade de Coimbra
r2 (f)f2
Ar2
A2
C2
O2
Br2
Pr2
B2
rr2
P2
X
O1 C1
f1
A1
r1
P
B1 1