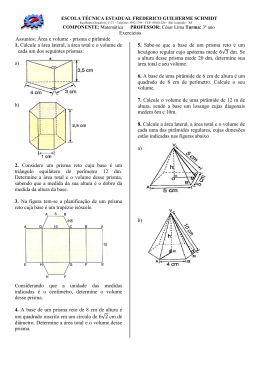
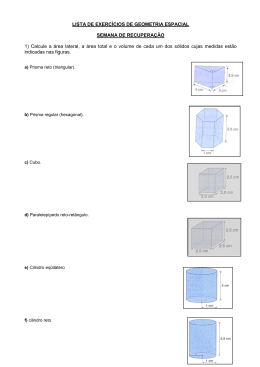
Lista de Exercícios de Recuperação de MATEMÁTICA 2
NOME_________________________________________________________ Nº_______ SÉRIE:
DATA 3° BIMESTRE
PROFESSOR : Denis Rocha_____________ DISCIPLINA : Matemática 2_______
2° EM__
1)
Uma prova tem 4 testes com 5 alternativas cada um. Respondendo aleatoriamente às questões, qual
é a probabilidade de gabaritar a prova?
2) Escolhendo-se ao acaso duas arestas de um cubo, qual a probabilidade de elas serem reversas?
3) Um grupo de 100 universitários é formado por 52 estudantes de Engenharia, 27 de Medicina, 10 de
Filosofia e os demais de Direito. Escolhido ao acaso um elemento do grupo, qual é a probabilidade de ele
ser estudante de Engenharia ou Medicina?
4) Um dado é jogado três vezes, uma após a outra. Pergunta-se: Quantos são as possibilidades onde os
três resultados são diferentes?
5) Considere todas as permutações de cinco letras da sigla PUCRS. Umas dessas permutações foi
escolhida ao acaso. Calcule a probabilidade de a escolhida terminar com a letra C e começar com a letra
P.
6) (UNICAMP) Um dado é jogado 3 vezes, uma após a outra. Qual é a probabilidade de a soma dos
resultados ser maior ou igual a 16?
7) Uma urna tem 100 cartões numerados de 101 a 200. Calcule a probabilidade de se sortear um cartão
dessa urna e o número nele marcado ter os três algarismos distintos entre si.
8) (VUNESP) Um baralho tem 13 cartas das quais 4 são ases. Retiram-se 3 cartas ao acaso. Qual é a
probabilidade de haver pelo menos um ás entre as cartas retiradas?
9) Em um jogo de pôquer têm-se 32 cartas, 8 de cada um dos naipes. Um jogador recebe 5 cartas. Qual
é a probabilidade de que todas sejam do mesmo naipe?
10) (UEL) No diagrama a seguir, o espaço amostral S representa um grupo de amigos que farão uma
viagem. O conjunto A indica a quantidade de pessoas que já foram a Maceió e o conjunto B, a quantidade
de pessoas que já foram a Fortaleza.
A empresa de turismo que está organizando a viagem fará o sorteio de uma passagem gratuita.
Considerando que a pessoa sorteada já tenha ido para Fortaleza, calcule a probabilidade de que ela
também já tenha ido para Maceió.
S
B
A
11) Em três lançamentos consecutivos de um dado perfeito, a probabilidade de que a face 6 apareça
voltada para cima em pelo menos um dos lançamentos é:
12) A altura de um prisma reto mede 12 cm e a base é um triângulo cujos lados medem 10 cm, 8 cm e 6
cm. Calcular a área lateral do prisma.
13)
2
Determine o volume de um cubo cuja área da base é igual a 36 cm .
14) Um prisma heptagonal regular tem arestas da base que medem 3 3 cm e altura de 5 2 cm .
Determine a sua área lateral.
15) Um paralelepípedo reto tem como base um retângulo de lados 5 cm e 12 cm e o seu volume é 420
cm 2 . Determine a diagonal da base, a altura e a área total desse prisma.
h
5 cm
12 cm
2
16) Um prisma tem como base um quadrado de lado 5 cm e a sua área total é 450 cm . Determine a
altura e volume desse prisma.
h
5
5
17) Um prisma hexagonal regular tem 15 cm de altura e a maior diagonal da base mede 6 cm. Determinar
a área total desse prisma.
18) Um prisma octogonal regular tem 4
Calcular a área lateral desse prisma.
3 cm de altura e a aresta da base 7 cm.
19) Um prisma triangular regular tem 2 3 cm de aresta da base. Sabendo que a medida da aresta lateral
é o triplo da medida da aresta da base, calcule:
a.) a área da base;
b.) a área lateral.
20) Um arquiteto tem dois projetos para a construção de uma piscina retangular com 1 m de
profundidade:
Projeto 1: dimensões do retângulo: 16 m x 25 m.
Projeto 2: dimensões do retângulo: 10 m x 40 m.
Sabendo que as paredes e o fundo da piscina são revestidos com azulejos cujo preço é R$ 20,50 o metro
quadrado, calcule qual a despesa com azulejos:
a.)
21)
no projeto
B) no projeto 2.
A diagonal de um cubo mede 10 3 cm, determine:
a) a sua área total;
b) o seu volume.
22) A base de um prisma reto é um triângulo isósceles com lados medindo 10 cm, 10 cm e 12 cm e o
3
seu volume é igual a 960 cm . Determine a altura do prisma.
10
10
h
10
10
12
23)
24)
A aresta de um cubo mede 8 dm . Determine a diagonal, a área total e o volume do cubo.
O cubo de vértices ABCDEFGH, indicado na figura, tem arestas de comprimento 12 cm.
Sabendo que M é o ponto médio da aresta AE e N é o centro do quadrado ABCD, Determine:
a) O volume do cubo;
b) A medida da diagonal do cubo;
c) A distância entre os pontos M e N.
25) O perímetro da base de um prisma de base quadrada é igual a 4 cm e a sua altura á 12 cm.
a) Determine a medida da aresta da base;
b) O volume do prisma.
26) Uma piscina vai ser revestida com azulejos que custam R$ 19,50 o m2. As dimensões da piscina são
10 m de comprimento por 6,5 m de largura e 1 m de profundidade. Determine quanto será gasto em
azulejos para revestir a piscina.
TESTES: ASSINALE AS RESPOSTAS NO GABARITO E DEIXE TODOS OS CÁLCULOS
27) (ENEM) Uma das principais causas de degradação de peixes frescos é a contaminação por bactérias.
O gráfico apresenta resultados de um estudo acerca da temperatura de peixes frescos vendidos em cinco
peixarias. O ideal é que esses peixes sejam vendidos com temperaturas entre 2°C e 4°C. Selecionando-se
aleatoriamente uma das cinco peixarias pesquisadas,
a probabilidade de ela vender peixes frescos na
condição ideal é igual a:
a)
b)
c)
d)
e)
1
2
1
3
1
4
1
5
1
6
28)
(ENEM) Em um concurso de televisão, apresentam-se ao participante 3 fichas voltadas para baixo,
estando representada em cada uma as letras T, V e E. As fichas encontram-se alinhadas em uma ordem
qualquer. O participante deve ordenar as fichas ao seu gosto, mantendo as letras voltadas para baixo,
tentando obter a sigla TVE. Ao desvirá-las, para cada letra que esteja na posição correta ganhará um
prêmio de R$ 200,00.
A probabilidade de o participante não ganhar qualquer prêmio é igua a:
a) 0
1
3
1
c)
4
1
d)
2
1
e)
6
b)
29) A vida na rua como ela é
O Ministério do Desenvolvimento Social e Combate à Fome (MDS) realizou, em parceria com a ONU, uma
pesquisa nacional sobre a população que vive na rua, tendo sido ouvidas 31.922 pessoas em 71 cidades
brasileiras. Nesse levantamento, constatou-se que a maioria dessa população sabe ler e escrever (74%),
que apenas 15,1% vivem de esmolas e que, entre os moradores de rua que ingressaram no ensino
superior, 0,7% se diplomou. Outros dados da pesquisa são apresentados nos quadros abaixo.
No universo pesquisado, considere que P seja o conjunto das pessoas que vivem na rua por motivos de
alcoolismo/drogas e Q seja o conjunto daquelas cujo motivo para viverem na rua é a decepção amorosa.
Escolhendo-se ao acaso uma pessoa no grupo pesquisado e supondo-se que seja igual a 40% a
probabilidade de que essa pessoa faça parte do conjunto P ou do conjunto
Q, então a probabilidade de que ela faça parte do conjunto interseção de P e Q é igual a
a)
16%
b)
52%
c)
12%
d)
20%
e)
36%
30) A população brasileira sabe, pelo menos intuitivamente, que a probabilidade de acertar as seis
dezenas da mega sena não é zero, mas é quase. Mesmo assim, milhões de pessoas são atraídas por essa
loteria, especialmente quando o prêmio se acumula em valores altos. Até junho de 2009, cada aposta de
seis dezenas, pertencentes ao conjunto {01, 02, 03, ..., 59, 60}, custava R$ 1,50. (Disponível em:
www.caixa.gov.br. Acesso em: 7 jul. 2009.)
Considere que uma pessoa decida apostar exatamente R$ 126,00 e que esteja mais interessada em
acertar apenas cinco das seis dezenas da mega sena, justamente pela dificuldade desta última. Nesse
caso, é melhor que essa pessoa faça 84 apostas de seis dezenas diferentes, que não tenham cinco
números em comum, do que uma única aposta com nove dezenas, porque a probabilidade de acertar a
quina no segundo caso em relação ao primeiro é, aproximadamente
a)
b)
c)
d)
e)
1
vez maior
2
1
2 vez maior
2
1
4 vezes menor
9 vezes menor
14 vezes menor
31) (UFRRJ/RJ) Observe o bloco retangular da figura 1, de vidro totalmente fechado com água dentro.
Virando-o, como mostra a figura 2, podemos afirmar que o valor de x é:
a)
12 cm
b)
11 cm
c)
10 cm
d)
5 cm
e) 6
cm
11) (PUC-PR) O volume de um prisma hexagonal de altura 5 m é 30 3 m3 . Calcule a aresta da base do
prisma, em m :
a)
b)
c)
d)
e)
5
4
3
2
1
32) Uma piscina tem a forma de um prisma reto cuja base é um retângulo de dimensões 15 m e 10 m. A
quantidade necessária de litros de água para que o nível de água da piscina suba 10 cm é:
a) 0,15 L
b) 1,5 L
c) 150 L
d) 1500 L
e) 15000 L
33) (PUC/CAMP) Usando uma folha de latão, deseja-se
de 8 dm³. A área da folha utilizada para isso será, no mínimo:
construir
um
cubo
com
volume
a) 20 cm²
b) 40 cm²
c) 240 cm²
d) 2000 cm²
e) 2400 cm²
34)
Dois blocos de alumínio, em forma de cubo, com arestas medindo 10 cm e 6 cm são levados
juntos à fusão e em seguida o alumínio líquido é moldado como um paralelepípedo reto de arestas 8 cm, 8
cm e x cm. O valor de x é:
a) 16
b) 17
c) 18
d) 19
e) 20
35)
Considere o sólido resultante de um paralelepípedo retângulo de arestas medindo x , x e 2x ,
do qual um prisma de base quadrada de lado 1 e altura x foi retirado. O sólido que foi retirado está
representado pela parte escura da figura.
1
1
x
O volume desse sólido, em função de x , é dado pela expressão:
a) 2x 3  x 2
b) 4x 3  x
c) 2x 3  x
d) 2x 3  2x 2
e) 2x 3  2x
A
B
C
D
E
27
A
B
C
D
E
28
A
B
C
D
E
29
A
B
C
D
E
30
A
B
C
D
E
GABARITO
31
A
B
C
D
E
32
A
B
C
D
E
2x
33
A
B
C
D
E
34
A
B
C
D
E
x
35
A
B
C
D
E