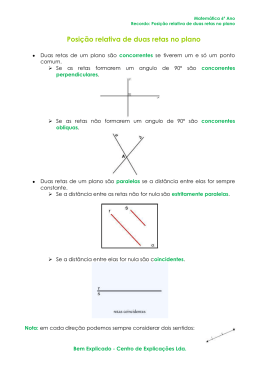
AULA DE REPOSIÇÃO 002 / 3º ANO
Posições relativas entre duas retas
No plano, retas podem ter 3 posições relativas:
•
•
•
Paralelas: não possuem intersecção
Coincidentes: Se interceptam em todos os pontos (são a mesma reta)
Concorrentes: Se interceptam em um único ponto
o Oblíquas: Quando o ângulo entre as retas difere de 90º
o Perpendiculares: Quando o ângulo entre as retas é 90º
Retas Paralelas
Duas retas são paralelas quando possuem mesmo coeficiente angular e
coeficientes lineares diferentes.
Exemplo:
r : y = −2 x + 10
s : y = −2 x − 28
Os coeficientes angulares de r e s são iguais: m = −2
Os coeficientes lineares de r e s são diferentes: nr = 10 e n s = −28
Portanto, as retas são paralelas
Retas Coincidentes
Duas retas são coincidentes quando possuem coeficientes angular e linear iguais.
Exemplo:
r : y = 5x + 6
s : 10 x − 2 y + 12
Os coeficientes angulares de r e s são iguais: m = 5
Os coeficientes lineares de r e s são diferentes: n r = n s = 6
Portanto, as retas são coincidentes, ou seja, são a mesma reta
Retas Perpendiculares
Duas retas são perpendiculares quando seus coeficientes angulares são opostos e
inversos. O perpendicularismo de retas independe de seus coeficientes lineares.
r : y = 2x + 9
1
Exemplo:
s: y =− x−4
2
Os coeficientes angulares de r e s são opostos e inversos: mr = 2 , m s = −
1
2
Portanto, as retas são perpendiculares, ou seja, formam um ângulo de 90º
Retas Oblíquas (e não perpendiculares)
Duas retas são oblíquas quando possuem coeficientes angulares diferentes.
Exemplo:
r : y = 3x + 7
s : y = 4x − 5
Os coeficientes angulares de r e s são diferentes: mr = 3 , m s = 4
Portanto, as retas são obliquas, ou seja, interceptam-se em um único pontos e não
formam um ângulo de 90º
Exercícios:
01. Dê as posições relativas das retas
r : 3x − y + 2 = 0
x y
s:
+
=1
4 10
2x
t:
y=
−1
3
u : 4x − 6 y + 5 = 0
nas comparações:
a) r e s
b) r e t
c) r e u
d) s e t
e) s e u
f) u e t
02. Determine a equação geral da reta que passa pelo ponto P = (2,−3) e é paralela à
reta r : 5 x − 2 y + 1 = 0
Respostas: 01. a) oblíquas, b) oblíquas, c) oblíquas, d) oblíquas, e) oblíquas,
5x
− y −8 = 0
f) paralelas. 02. s :
2
DESAFIO: No movimento de rotação, a Terra gira em torno do próprio eixo, e na linha
do Equador a velocidade desse movimento é de, aproximadamente, 1668,91 km/h. Qual
é, aproximadamente, o raio da Terra?
Perguntas do professor:
1. Com os dados do problema, é possível resolvê-lo?
2. Porquê a palavra aproximadamente está enfaticamente destacada no problema?
* Para lhe ajudar a responder estas perguntas, assista ao vídeo do link abaixo. Ele traz
algumas rotações do Planeta Terra, visto sem água:
https://www.youtube.com/watch?v=PK0Vmhw6jqU
Distância entre Ponto e Reta
Fora de uma reta, sabemos que existem infinitos pontos. Porém, estabelece-se
que a menor distância entre um ponto e uma reta é um segmento perpendicular à reta,
que passa por este ponto. Assim:
d ( P, r ) =
| ax P + by P + c |
a2 + b2
Exemplo: Qual a distância entre o ponto P = (3,5) e a reta r : x + 2 y − 8 = 0 ?
Resolução:
a =1
b=2
c = −8
xP = 3
yP = 5
Assim: d ( P, r ) =
d ( P, r ) =
| ax P + by P + c |
a2 + b2
| 1.3 + 2.5 − 8 |
12 + 2 2
=
| 3 + 10 − 8 |
1+ 4
=
|5|
5
=
5
5