Hamiltonianos e Equações Canônicas.
- Já havíamos observado o seguinte fato: ao calcular a derivada temporal “convectiva” de um
Lagrangeano L=L q , q̇ ,t  (fixemo-nos por enquanto em um sistema de 1 grau de liberdade),
obtemos
dL ∂ L
∂L
∂L
=
q̇
q̈
,
dt ∂ q
∂ q̇
∂t
(1)
o qual, com auxílio da Eq. Dde Euler-Lagrange d / dt ∂ L/ q̇=∂ L/ ∂ q , pode ser reescrita nas formas
 
dL d ∂ L
∂L
∂L d
∂L ∂L
=
q̇
q̈
=
q̇

.
dt dt ∂ q̇
∂ q̇
∂ t dt ∂ q̇
∂t
(2)
Isto implica na igualdade


d
∂L ∂L
L −q̇
=
,
dt
∂ q̇
∂t
(3)
que nos informa ser a quantidade E≡ q̇ ∂ L/ ∂ q̇− L uma constante de movimento sempre que o
tempo não comparecer explícitamente no Lagrangeano.
- Para Lagrangeanos do tipo
se U(x,t) = U(x).
2
L=m / 2 ẋ – U  x , t  ,
2
E=m/ 2 ẋ U  x ,t  , onde E será constante
- Seria no mínimo curioso transitar de uma formulação onde L seja a função básica de onde se extraem
as equações de movimento, para uma onde E seja esta função básica. Para tanto, vamos seguir os
seguintes passos:
∂ L  q , q̇ ,t 
≡p;
(i) Definamos
∂ q̇
E= q̇ p – L .
∂L
∂L
dq –
d q̇ ,
(iii). Calculemos o diferencial de E: dE =d q̇ pq̇ dp –
∂q
∂ q̇
(ii) Reintroduzamos o conceito de E na forma
o que, de acordo com (i) pode ser escrito como
dE =q̇ dp –
∂L
dq .
∂q
(4)
- Se E pudesse ser escrito explicitamente como uma função de p e q, de (4) poderíamos diretamente
interpretar dE como uma forma diferencial para a qual valem as relações
∂E
, (5)
∂p
−∂ L ∂ E
=
. (6)
∂q
∂q
q̇=
- O que acontece é que é de fato possível escrever E unicamente em termos de q e p, porque através de
(i) sabemos como expressar q̇ em termos de q e p! Conclusão: as expressões (5) e (6) são
perfeitamente válidas.
- As expressões (5) e (6) valem para valores genéricos de q e p. Mas ha mais! Se estivermos
“perseguindo” uma partícula, então vale e equação de Euler-Lagrange ṗ=∂ L/∂ q . Com isto, se
então estivermos integrando a órbita física de uma partícula, as expressões (5) e (6) assumem a assim
chamada forma canônica:
∂H
, (7)
∂p
∂H
ṗ=−
, (8)
∂q
q̇=
onde por uma questão de tradição designamos E como H(p,q,t), o assim chamado “Hamiltoniano” do
sistema.
- Na formulação Lagrangeana, as trajetórias de movimento eram extraídas de uma equação diferencial
de segunda ordem. Na formulação Hamiltoniana, as equações são duas de primeira ordem o que é
totalmente equivalente à formulação anterior.
- Explo.: Suponham um Lagrangeano do tipo L=m / 2 ẋ 2 – U  x , t . Como gerar o Hamiltoniano?
Bem, como primeiro passo, definir p≡∂ L/ ∂ ẋ=m ẋ . A seguir, construir H={dot x} p – m/2 {dot
x}^2 + U(x,t) , o que, usando a definição de p para escrever ẋ em termos de p e x, nos dá:
H = p2 /2m U  x ,t  . As equações de movimento (7) e (8) de pronto nos fornecem
∂H p
=
, (9)
∂p m
∂H
∂U
ṗ=−
=−
. (10)
∂x
∂x
ẋ=
Derivando mais uma vez a (9) e usando (10) finalmente terminamos com
ẍ=−
1 ∂U
,
m ∂x
(11)
que é a equação de “força” obtida diretamente da formulação Lagrangeana.
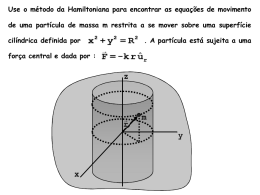
- Problema: Como fica a formulação Hamiltoniana em várias dimensões?
- Problema: Como fica o caso de uma partícula atraída por um campo central em 2D, como já
analisado anteriormente ( L=m / 2  ẋ 2 ẏ 2  – U   x 2 y 2  )?