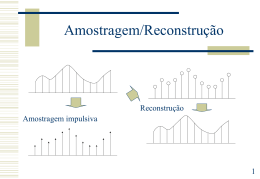
Teorema de Amostragem
xs (t )  xc (t )s(t )
Ou critério de Nyquist
Transformada de um pente de diracs é um pente de diracs:
2 
s(t )    (t  nT )  S ( j) 
 (  k. S )

T k 
k  
1
1 
X S ( j) 
X C ( j) * S ( j)   X C ( j (  k. S ))
2
T k 

TF
O espectro do sinal
amostrado é uma soma de
réplicas do sinal continuo
deslocadas na frequência.
Notar que:
2  ()   ( f )
  2 f / f a
  2 f
A reconstrução do sinal contínuo é
possível desde que:
S  2N  Fa  2FN
1
Teorema de Amostragem
Sem Sobreposição
espectral
(aliasing)
Espectro do sinal
contínuo
Espectro de uma
sequência de
diracs
Amostragem
Sobreposição
espectral
(aliasing)
2
Reconstrução
Amostragem
Reconstrução
É possível
através de um
filtro passa
baixo desde
que exista
sobreposição
espectral
S  2 N
3
Reconstrução
xs (t ) 

 x[n] (t  nT )
h(t ) 
k  

y(t )  xs (t ) * h(t )   x[n]h(t  nT )
sin[ t / T ]
t /T
k  
Vale zero nos pontos
correspondentes às
restantes amostras
Filtro de
reconstrução
ideal
Soma de
Sincs
4
Sub/Sobre-Amostragem
 Sub Amostragem: Redução da
frequência de amostragem.
Teorema da
Amostragem
v[n]  x[ M .n]
 Sobre Amostragem: Aumento da
frequência de amostragem.
v[n] 

  [n  kM ]x[k ]
Nota: não é, em
geral, equivalente a
amostrar a uma
frequência superior
k  
5
Processamento de Sinais
contínuos
Filtro AntiSobreposição de
espectro
Amostragem e
retensão
Conversor
Analógico para
Digital
Processador
Digital de Sinais
Filtro de
reconstrução
retenção de
ordem zero
Anti-aliasing filter
Sample and Hold
(SH)
Conversor
Analógico para
Digital
Analog to Digital
(A/D)
DSP
Reconstruction
Filter
Zero Order Hold
(ZOH)
Digital to Analog
(DA)
6
Resposta em Frequência
 O processamento de sinais contínuos através de
sistemas discretos (digitais) conduz a sistemas
que são apenas aproximadamente invariantes
no tempo!
  2f / f a
xs (t )  xc (t )s(t )
 No entanto quando podemos aplicar o critério de Nyquist:
Frequência
normalizada

Ys ( f )
jω

 H s ( f )  H A ( f ) H(e )
f

ω

2π
Xs( f )
fa

H A ( f ),- Filtroanti- sobreposição de espectro
H ( f )  H(e jω )
f ,- Respostaem frequênciado sistema discreto
ω 2π
fa
H R ( f ),- Filtrode reconstrução

H R ( f )


  2 f
7
Exemplo: Implementação de um
Atraso Fraccionário
 Atraso Fraccionário: Um atraso que não é múltiplo da
frequência de amostragem. nT
Assumindo filtros de anti-aliasing e de reconstrução ideais:
 


  n  
sin





2
f
1
a 

 j  / f a

h[n] 
e
d 

2 
n
H S ( f )  e2 f   H (e j )  e / fa
O que corresponde a um impulso para atrasos inteiros, e a um sinc
amostrado para atrasos fraccionários.
Notar que é possível facilitar a implementação se não se exigir a
correspondência ao atraso em toda a banda.
8
Amostragem e Retenção
 A reconstrução é normalmente efectuada utilizando
retentores de ordem zero.
Amostragem
Retenção de
ordem zero (ZOH)
9
Compensação de ZOH
 ZOH
 Saída é convulsionada,
t
Y  f   Y '  f T sinc f / T 
y(t )  y' (t ) * rect 
T 
 Solução: Pre-filtrar o sinal por um filtro cuja função de
transferência seja a inversa deste na banda de passagem!
10
Amostragem de Sinais Passa-banda
Sinal Real
B
Para sinais
complexos
temos Fa=B!!
Amostragem
No melhor caso; para
certos valores pré
determinados
Distância entre réplicas:
2B = Fa
11