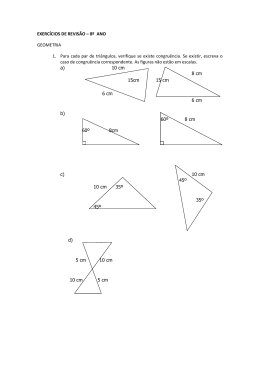
Congruência de Triângulos
• Triângulos congruentes
• Casos de congruência
– Caso LLL (lado, lado, lado)
– Caso LAL (lado, ângulo, lado)
– Caso ALA (ângulo, lado, ângulo)
• Outras situações
– Não há caso AAA
– Não há caso LLA
O que acontece quando dois triângulos são
congruentes (iguais)?
Se dois triângulos são congruentes, verifica-se que:
C
F
D
A
E
B
- os lados são congruentes:
,
e
AB  DF
AC  DE
;
BC  EF
- os ângulos são congruentes:
,
BAC  EDF ABC  DFE
e
.
ACB  DEF
Quando sabemos que dois triângulos são
congruentes?
Existem condições mínimas a verificar para garantir que
dois triângulos são congruentes.
A essas condições chamamos
CASOS DE CONGRUÊNCIA DE TRIÂNGULOS.
Caso LLL (lado, lado, lado)
Consideremos dois triângulos, dos quais se conhecem os
comprimentos dos lados.
F
D
C
E
A
Verifica-se que:
B
AB  DF
AC  EF
BC  DE
Dois triângulos são congruentes se tiverem os três lados
correspondentes congruentes.
Caso LAL (lado, ângulo, lado)
Consideremos dois triângulos, dos quais se conhecem os
comprimentos de dois dos seus lados e a amplitude do
ângulo entre eles.
C
E
A
B
D
Verifica-se que:
AC  EF
F
BC  DE ACB  DEF
Dois triângulos são congruentes se tiverem dois lados
correspondentes congruentes e o ângulo por eles
formado congruente.
Caso ALA (ângulo, lado, ângulo)
Consideremos dois triângulos, dos quais se conhece o
comprimento de um dos lados e as amplitudes de dos
dois ângulos que lhe são adjacentes.
D
F
C
E
A
Verifica-se que:
B
AB  DF
BAC  EDF ABC  DFE
Dois triângulos são congruentes quando têm um lado
congruente e os dois ângulos que lhe sejam adjacentes
congruentes.
Haverá mais casos de congruência de
triângulos?
Para um triângulo qualquer, não existem mais casos de
congruência de triângulos.
Vejamos algumas situações que são por vezes,
erradamente, consideradas como casos de congruência.
Mas não o são!...
Não há caso AAA!...
Consideremos dois triângulos, dos quais se conhecem as
amplitudes dos seus ângulos.
Verifica-se que se podem construir muitos triângulos que
não são congruentes.
Assim, não podemos garantir, sem qualquer dúvida, que
os triângulos dados são congruentes.
Não há caso LLA!...
Consideremos dois triângulos, dos quais se conhecem os
comprimentos de dois dos seus lados e a amplitude de um
ângulo adjacente apenas a um dos lados.
Verifica-se que se podem construir dois triângulos que não
são congruentes entre si.
Assim, não podemos garantir, sem qualquer dúvida, que os
triângulos dados são congruentes.