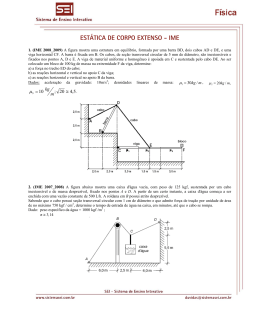
Matrizes – IME
1. (IME) Determine uma matriz
não singular P que satisfaça à equação
⎡6 0 ⎤
P-1 A = ⎢
⎥,
⎣0 −1⎦
matricial
⎡1 2⎤
onde A = ⎢
⎥.
⎣5 4⎦
2. (IME) Considere a matriz A = (akj), onde:
akj = k-ésimo termo do desenvolvimento de (1 + ji)54,
com k = 1, ..., 55; j = 1,..., 55 e i =
−1 .
a) Calcule a3,2 + a54,1
b) Determine o somatório dos elementos da coluna 55
c) Obtenha uma fórmula geral para os elementos da diagonal principal.
3. (IME) Considere uma matriz A, n x n, de coeficientes reais, e k um número real diferente de 1. Sabendo-se que A3 = k A,
prove que a matriz A + I é invertível, onde I é a matriz identidade n x n.
4. (IME) Determine todas as matrizes X, reais, de dimensões 2 x 2, tais que AX = XA, para toda matriz A real 2 x 2.
5. (IME) Sejam A, B e C matrizes 5 x 5, com elementos reais. Denotando-se por At a matriz transposta de A,
a) Mostre que se AAt = 0, então A = 0
b) Mostre que se BAAt = CAAt então BA = CA.
6. (IME) Sejam
⎛a
⎜
⎜c
A= ⎜
⎜e
⎜g
⎝
b⎞
⎟
d⎟
e B=
f ⎟⎟
h ⎟⎠
⎛ i j l m⎞
⎜⎜
⎟⎟ .
⎝n o p q ⎠
Duas matrizes de elementos inteiros. Verifique se a matriz AB é inversível.
7. (IME) Dada a matriz M = (mij )
⎡1 0 1 1⎤
⎢0 1 0 1⎥
⎥
M= ⎢
⎢1 0 1 1⎥
⎢
⎥
⎣1 1 1 1⎦
e o conjunto A = {a1; a2; a3; a4}, define-se em A uma relação R por:
ai R aj ⇔ mij = 1
Verifique se R é uma relação de equivalência.
8. (IME) Seja Mn(R) o conjunto de matrizes quadradas de ordem n, de coeficientes reais. Define-se a função,
Ψ : Mn(R) x Mn(R) Æ Mn(R)
Ψ (A,B) = AB – BA
Calcule:
Ψ (Ψ(A,B);C) + Ψ (Ψ(B,C),A) + Ψ(Ψ(C,A),B)