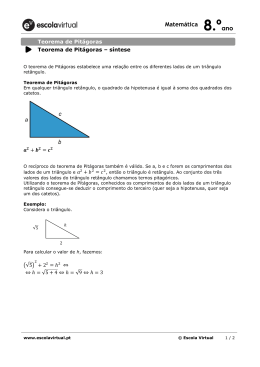
Teorema de Pitágoras
Este é um roteiro que pode ser desenvolvido
em sala de aula para ajudar na aprendizagem
sobre o Teorema de Pitágoras.
O Teorema de Pitágoras talvez seja o mais importante teorema de toda a matemática. Por esta razão,
talvez seja o que possui maior número de demonstrações diferentes.
Para começar a estudar o teorema, talvez seja interessante saber um pouco mais sobre o seu criador.
Quem foi Pitágoras? Lá no site Só Matemática! em http://www.somatematica.com.br/biograf/pit.php se
pode saber mais sobre ele.
Para demonstrar que o teorema de Pitágoras é verdadeiro se propõe a seguinte atividade com os
alunos na sala de aula.
Participantes: é indicado que a sala seja dividida em 5 grupos, para o manuseio.
Material utilizado: o modelo é constituído por um triângulo retângulo e dois quadrados sendo os
lados de um deles congruentes ao cateto menor e os lados do outro congruentes ao cateto maior.
Veja no manuseio como esse modelo foi construído.
Objetivo: mostrar que o quadrado da hipotenusa de um triângulo retângulo é igual à soma dos
quadrados dos catetos.
Resolução: a partir de um triângulo ABC, retângulo em A, traçamos a altura AH e verificamos que
os triângulos AHB e AHC são semelhantes ao triângulo ABC.
Da semelhança dos triângulos AHB e ABC temos b² = am e da semelhança dos triângulos AHC e
ABC temos c² = an. Somando essas duas relações membro a membro, encontramos:
b² + c² = am + an = a(m + n) a * a = a² (esta é a prova algébrica do teorema).
Manuseio: podemos também provar o teorema manuseando triângulos e quadrados recortados em
cartolina da seguinte forma: temos dois quadrados, um de lado b e outro de lado c. Tais medidas, b
e c, são medidas dos catetos de um triângulo retângulo. Vamos juntar as áreas (b² e c²) e formar um
novo quadrado de lado a, que é a medida da hipotenusa do mesmo quadrado.
Vale a pena ver alguns vídeos que demonstram o teorema:
•
O Barato de Pitágoras é um vídeo produzido pela TV Escola, muito bom, e pode ser encontrado
no endereço http://bit.ly/95d2Mq . Ele tem tempo de exibição = 14,14 min e pode fazer a ligação
com modelo concreto de matemática
• Vídeo do LEMA-UFBA usando um outro material manipulável
em http://www.youtube.com/watch?v=JC2GSPskAds
• Vídeo da demonstração do teorema utilizando água em
http://www.youtube.com/watch?v=hTxqdyGjtsA
• Demonstração do teorema com dobraduras de cubos em
http://www.youtube.com/watch?v=OGJYj5O83oU
As ilustrações interativas também são interessantes:
- Entendendo Pitágoras http://homes.dcc.ufba.br/~frieda/entendendopitagoras/
- Pitágoras Net http://www.pitagorasnet.com/pitagorasNet.html/
- Uma demonstração http://bit.ly/d7YwCy
- Outra demonstração http://bit.ly/95V94a
Aplicações no dia-a-dia do teorema:
- http://bit.ly/aGitx2 - teleaula com exemplos de como aplicar o Teorema de Pitágoras.
- http://bit.ly/af8AW3 - exercícios do Teorema de Pitágoras no Cotidiano
Exercícios:
- http://pacascarnaxide.tripod.com/Exercicios.htm
- http://www.educ.fc.ul.pt/icm/icm98/icm14/aplicacoes.htm
- http://www.prof2000.pt/users/hjco/Pitagora/pg000011.htm
Curiosidades:
• WebSurf PITÁGORAS http://bit.ly/9VfHq9 é uma webquest sobre o tema que pode
estimular os alunos a aprender mais;
• Perímetros Pitagóricos e outros http://www.prof2000.pt/users/paulap/problemas.html .
• História da Matemática na Índia http://www.malhatlantica.pt/mathis/India/BhaskaraII-7.htm
E para avançar mais:
Como localizar um número irracional na reta usando o Teorema de Pitágoras em http://bit.ly/dzSOxt
Esta atividade foi desenvolvida pela
Profa Frieda para o Projeto Educandow e
contou com a colaboração da aluna de
Matemática da UFBA, Jamille Vilas Boas.
Outubro/2010