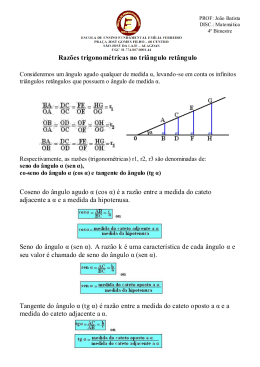
340
O ENSINO DE TRIGONOMETRIA: A BUSCA DE NOVOS
CAMINHOS
Jenifer Lunara da Silva (UNI-FACEF)
Introdução: Nosso trabalho de iniciação cientifica se inicia motivado pelas nossas
dificuldades no aprendizado desse conteúdo, assim como muitos alunos que cursam
a educação básica. A Trigonometria está presente em nosso cotidiano, ela não se
limita ao estudo somente de triângulos. Suas aplicações são utilizadas em diversos
campos da Matemática, por isso a importância de seu ensino aprendizado.
Conceitos Básicos de Trigonometria
Todo triângulo que tem um ângulo de 90°(ângulo reto ) é denominado triângulo
retângulo. O triângulo ABC tem um ângulo reto e é denominado triângulo retângulo:
Onde:
a: hipotenusa;
b e c: catetos;
h: altura relativa à hipotenusa;
m e n: projeções ortogonais dos catetos sobre a hipotenusa.
341
Seno
Considere o ciclo trigonométrico (circulo de raio unitário, r = 1) no qual marcamos
o ponto M, que é imagem, no ciclo, do número real θ, conforme é mostrado na figura a
seguir.
O arco AM corresponde ao ângulo central θ.
Seja OM o raio do ciclo, e M” e M’ as projeções do ponto nos eixos y e x,
respectivamente.
Definimos como seno do ângulo (ou do arco AM) a ordenada do ponto M, e é
indicado como:
sen θ = OM”, sendo OM” a ordenada do ponto M.
Agora observe o triângulo retângulo OM’M. Também podemos definir o seno do
ângulo θ como sendo a razão entre o cateto oposto ao ângulo θ e a hipotenusa do
triângulo OM’M. Veja:
sen θ =
sen α =
M ' M OM "
=
= OM” ∴ sen θ = OM”
OM
1
cateto oposto
hipotenusa
Valores importantes de sen θ:
342
Cosseno
Considere o ciclo trigonométrico (circulo de raio unitário, r = 1) no qual
marcamos o ponto M, que é imagem, no ciclo, do número real θ, conforme é
mostrado na figura a seguir:
O arco AM corresponde ao ângulo central θ.
Seja OM o raio do ciclo, e M” e M’ as projeções do ponto M nos eixos y e x,
respectivamente.
Definimos como cosseno do ângulo θ (ou do arco AM) a abscissa do ponto M,
e é indicado como:
cos θ = OM’, sendo OM’ a abscissa do ponto M.
Agora observe o triângulo retângulo OM’M. Também podemos definir o cosseno do
ângulo θ, como sendo a razão entre o cateto adjacente ao ângulo θ e a hipotenusa
do triângulo OM’M . Veja:
343
cos θ =
cos α =
OM ' OM '
=
=OM’∴ cos θ =OM’
OM
1
cateto adjacente
hipotenusa
Abaixo, os valores mais importantes de cos θ:
Tangente
Considere o ciclo trigonométrico (circulo de raio unitário, r = 1) e T a
intersecção da reta OM com o eixo das tangentes (reta perpendicular ao eixo x, que
passa pelo ponto A).
344
O arco AM corresponde ao ângulo central θ.
Definimos como tangente do ângulo θ (ou do arco AM) a medida algébrica do
segmento AT, e é indicado como:
tg θ = AT
Agora observe que o triângulo retângulo OM’M e OAT são semelhantes.
Portanto estabelecemos a relação:
OM ' M ' M
=
OA
AT
Sabemos que:
•
OM’ = cos θ
•
M’M = sen θ
•
AT = tg θ
•
OA = r = 1
portanto:
cos θ senθ
senθ
=
∴ tg θ =
1
tgθ
cos θ
tg α =
345
cateto oposto
cateto adjacente
Valores importantes de tg θ:
O Círculo Trigonométrico
Chama-se Círculo Trigonométrico, ao círculo orientado de raio unitário, cujo
centro é a origem do sistema de coordenadas cartesianas, conforme figura a seguir.
O círculo trigonométrico é orientado positivamente no sentido ABA’B’A. O
sentido AB’A’BA é considerado negativo. Assim, o arco AB (ângulo reto) mede 90º e
o arco AB’ mede -90º . O arco ABA’ (ângulo raso) mede 180º ( ou p radianos) e o
arco AB’A’ mede (-180º).
O arco de uma volta completa (ABA’B’A) mede 360º; O arco AB’A’BA mede (360º), ou seja, é um arco negativo. Já sabemos que 360º = 2 π radianos.
Podemos na Trigonometria, considerar arcos de mais de uma volta.
Sabendo que uma volta equivale a 360º, podemos facilmente reduzir qualquer arco à
primeira volta. Por exemplo, o arco de 12350º, para reduzi-lo à primeira volta, basta
dividi-lo por 360º (para eliminar as voltas completas) e considerar o resto da divisão.
Assim é que, 12350º dividido por 360º, resulta no quociente 34 e no resto 110º. Este
valor 110º é então trigonométricamente equivalente ao arco de 12350º e é
denominado sua menor determinação positiva.
346
Dois arcos trigonométricos são ditos côngruos, quando a diferença entre eles
é um número múltiplo de 360º . Assim é que sendo x e y dois arcos trigonométricos,
eles serão côngruos se e somente se x - y = k . 360º , onde k é um número inteiro.
Portanto, para descobrir se dois arcos são côngruos, basta verificar se a diferença
entre eles é um múltiplo de 360º (ou 2 π radianos, pois 2 π rad = 360º).
Os
arcos
2780º
-
2780º
1700º
e
1700º,
por
=
1080º
e
exemplo
1080º
é
são
côngruos,
divisível
por
pois
360º
(1080º / 360º = 3 , com resto nulo).
Figura 1- Círculo trigonométrico
Fonte: http://www.feferraz.net/br/P/Ciclo_Trigonometrico.
Funções Trigonométricas
As funções trigonométricas são funções angulares, importantes no estudo dos
triângulos e na modelação de fenômenos periódicos. Podem ser definidas como
347
razões entre dois lados de um triângulo retângulo em função de um ângulo, ou,
de forma mais geral, como razões de coordenadas de pontos no círculo unitário.
Função seno
O domínio dessa função é R e a imagem é Im [-1,1]; visto que, na
circunferência trigonométrica o raio é unitário.
Domínio de f(x) = sen x; D(sen x) = R.
Imagem de f(x) = sen x; Im(sen x) = [ -1,1] .
Sinal da Função:
Como seno x é a ordenada do ponto-extremidade do arco:
f(x) = sen x é positiva no 1° e 2° quadrantes (orde nada positiva)
f(x) = sen x é negativa no 3° e 4° quadrantes (orde nada negativa)
O gráfico dessa função é o seguinte:
Função Cosseno
O domínio dessa função é R e a imagem é Im [-1,1]; visto que, na
circunferência trigonométrica o raio é unitário.
348
Domínio de f(x) = cos x; D(cos x) = R.
Imagem de f(x) = cos x; Im(cos x) = [ -1,1] .
Sinal da Função:
Como cosseno x é a abscissa do ponto-extremidade do arco:
f(x) = cos x é positiva no 1° e 2° quadrantes (absc issa positiva)
f(x) = cos x é negativa no 3° e 4° quadrantes (absc issa negativa)
O gráfico dessa função é o seguinte:
Função Tangente
Domínio: A função da tangente apresenta uma peculiaridade. Ela não existe
quando o valor de cosx = 0 (não existe divisão por zero), portanto o domínio são
todos os números reais, exceto os que zeram o cosseno.
Conjunto Imagem: Ιm = ]− ∞, ∞[
Sinal da Função:
349
Como tangente x é a ordenada do ponto T interseção da reta que passa
pelo centro de uma circunferência trigonométrica e o ponto-extremidade do arco,
com o eixo das tangentes então:
f(x) = tg x é positiva no 1° e 3° quadrantes (produ to da ordenada pela abscissa
positiva)
f(x) = tg x é negativa no 2° e 4° quadrantes (produ to da ordenada pela abscissa
negativa)
O gráfico dessa função é o seguinte:
O domínio da função tangente é
e a imagem é o conjunto
R.
O ensino de trigonometria
Em nosso estudo sobre o ensino de trigonometria encontramos nas pesquisas
de Costa (1997), a preocupação em analisar qual a sequência didática mais propícia
350
para seu ensino. Para isso a pesquisadora usa dois grupos de alunos e duas
sequências didáticas: na primeira, a sequência se inicia com atividades no
computador e é finalizada com materiais manipulativos criados pela pesquisadora,
na segunda, ela faz o inverso. A autora conclui que o segundo grupo exposto a
segunda sequência obteve um melhor aproveitamento. Fundamentado na idéia de
Costa, o aprendizado das funções trigonométricas requer muita abstração do aluno,
porém, esse processo pode ser facilitado através de atividades manipulativas, que
ela nomeia de concretização. Isso é confirmado pelo segundo grupo que obteve
melhor aproveitamento.
Outras contribuições do trabalho citado são o estudo histórico e epistemológico
da trigonometria e o estudo e a evolução da noção de ângulo e das funções
trigonométricas. A autora produz diversos materiais didáticos que podem auxiliar
outros professores.
Analisando outras idéias, tendo como exemplo Mendes (2001), que sugere o
ensino de trigonometria a partir de tarefas estruturadas, obtidas no contexto da
história da matemática, como auxílio metodológico em sala de aula. Segundo o
autor, esses estudos possibilitam ao estudante a abordar temas não trabalhados por
eles. Mendes faz uso da história como agente facilitador do ensino, enfatizando
quatro opções de uso: biografia dos matemáticos; desenvolvimentos temáticos;
origem e significado dos termos matemáticos e estudos de textos do passado.
Mendes (2001 apud Fossa, 1995) aponta, ainda, a existência de várias
maneiras de se utilizar a história da matemática das quais ressaltamos: uso
ornamental, apontado para uma abordagem episódica ou novelesca; uso
ponderativo cujas circunstâncias com aspectos episódicos ou novelescos são
organizadas de maneira a permitir o uso manipulativo.
Ao trabalhar com a trigonometria, Nacarato (2003) explora as diversas
abordagens para a definição de seno contidos nos livros didáticos do século XX no
Brasil. Como consequência, a autora qualifica quatro grandes tendências para a
definição de seno:
A primeira prevaleceu até antes de 1930 e está diretamente ligada à
geometria euclidiana; a segunda está fundamentada no cálculo vetorial e predomina
até o final da década de 60; a terceira iniciou-se na década de 60 com o movimento
351
da matemática moderna, estendendo-se até a década de 80; a quarta tendência
é utilizada até os dias atuais e oscila entre uma ou outra tendência. A grande maioria
dos autores define o seno como sendo a razão entre a medida do cateto oposto e da
hipotenusa de um triângulo retângulo.
É importante ressaltar que não se pode empregá-las aleatoriamente, mas sim,
em concordância com as metas de ensino determinadas.
O trabalho realizado por Brito e Morey (2004), que tem como propósito
analisar as dificuldades em geometria e trigonometria, percebidas pelos professores
de Ensino Fundamental é sustentado num estudo feito por Fiorentini (1995) e
relacionam as diversas tendências que ocorrem no ensino da matemática no país: a
formalista clássica, a empírico-ativista, a formalista moderna, a tecnicista, a
construtivista e a sócio-etno-culturalista.
Nos anos 60, o movimento da matemática moderna introduziu a teoria dos
conjuntos na disciplina. Um dos efeitos da substituição da matemática axiomática
euclidiana por um modelo criado fora do país ocasionou o abandono do ensino de
trigonometria e geometria no Brasil.
No final da década de 80, quando houve um eminente esforço dos estudiosos
para mostrar a importância da trigonometria e geometria no ensino de primeiro grau,
houve uma forte resistência dos professores devido à deficiência no ensino desse
conteúdo existente na época da formação escolar e acadêmica dos mesmos. Assim,
o estudo da Geometria e da Trigonometria continuou fora das aulas de Matemática.
Para as autoras (BRITO E MOREY, 2004) alcançarem seu propósito,
aplicaram um curso de formação continuada para uma turma de 50 professores de
escolas estaduais do Rio Grande do Norte. Os resultados indicaram dificuldades nos
conceitos geométricos de altura e de semelhança, e também, nos conceitos
fundamentais da trigonometria.
Analisando as dificuldades encontradas pelos professores podemos
afirmar que tais dificuldades estão intimamente relacionadas à
formação escolar das décadas de 70 e 80 caracterizadas, entre
outros aspectos, pelo descaso para com a geometria e a
trigonometria, pela formalização precoce de conceitos geométricos e
trigonométricos
–
quando
esses
eram
estudados
-
e
pela
352
memorização de procedimentos sem a compreensão deles
(BRITO;MOREY, 2004, p.31).
Quando se considera a última Proposta Curricular para o Ensino de Matemática para
o Estado de São Paulo de 1992, esta apresenta o conteúdo trigonométrico como
situações de resoluções de problemas.
A história da trigonometria
Os primeiros indícios de noções de trigonometria surgiram tanto no Egito
quanto na Babilônia, provido do cálculo de razões entre números e entre lados de
triângulos semelhantes.
Isto pode ser observado no Papiro Ahmes, no Egito, é o maior documento
egípcio em matemática que chegou aos nossos dias. Ele é uma cópia de um antigo
papiro do século XIX a.C. que esteve em poder do escriba Ahmes. Foi adquirido no
Egito por H. Rhind e por isso é conhecido como Papiro Rhind. Ele contém 84
problemas, dos quais quatro fazem menção ao seqt de um ângulo.
Ahmes não foi claro ao exprimir o significado desta palavra, mas, pensa-se que
o seqt de uma pirâmide regular seja equivalente, hoje, à cotangente do ângulo OMV
(figura 1).
Exemplo:
Seja OV = 40 e OM = 80,
Então o seqt = 80 / 40,
Isto é: seqt = 2
353
Figura 2- seqt de uma pirâmide
Fonte:http://2.bp.blogspot.com/_ptcpJxeik4A/RjdGDa40aI/AAAAAAAAACc/HSRiu73
Efss/s320/desenho_tri_retangulo.Bmp.
Sabe-se que na construção das pirâmides era necessário manter uma
inclinação constante das faces, o que levou os egípcios a adotarem o conceito de
seqt, que representava a razão entre afastamento horizontal e elevação vertical.
Na índia ocorreram grandes descobertas na trigonometria, por conta da matemática
estar em desenvolvimento junto com outras ciências, determinando seis importantes
períodos, dos quais abordaremos apenas o clássico (400 d.C. a 1200 d.C.) em que a
trigonometria se desenvolveu, pois era considerada parte integrante da astronomia
pela necessidade e curiosidade de ser calculada a posição exata dos planetas.
Foram construídas tabelas de senos de diferentes arcos entre 0º e 90º. Nos estudos
dos matemáticos indianos, eram mais utilizadas a meia-corda, que mais tarde se
tornou o seno indianoi.
Os árabes também cooperaram muito com a trigonometria, com influências
indianas, persas e helenísticas. A partir dessas influências, e de muita criatividade,
os árabes desenvolveram o primeiro tratamento sistemático da trigonometria. Com
esse tratamento surgiram três importantes aspectos da trigonometria árabe: primeiro
a introdução de seis funções trigonométricas básicas; segundo a dedução da regra
do seno e o estabelecimento de outras identidades trigonométricas; e terceiro a
354
construção de tábuas trigonométricas detalhadas com a ajuda de vários
procedimentos de interpolação.
Na introdução das funções trigonométricas, a função seno foi incorporada na
trigonometria árabe vinda da Índia. Nesta época haviam dois tipos de trigonometria,
uma baseada na geometria das semicordas (invenção indiana), e outra com base na
geometria das cordas exemplificada no Almagesto de Ptolomeuii. Os árabes a partir
do século X, começando com Abul Wafa, usaram a função seno de um jeito mais
próximo da trigonometria moderna, apesar ser definida para um arco de circulo em
vez do ângulo central correspondente. As funções tangente e cotangente são de
origem árabe, já a secante e a cossecante quase não aparecem nas tabelas
trigonométricas existem, há poucas referências a elas nos trabalhos árabes, e uma
tradição da trigonometria fundamentada no comprimento de sombras é encontrada
tanto na matemática indiana como na árabe.
Sobre as relações trigonométricas a obra de Abul Wafa (grande matemático e
astrônomo em Bagdá) contém mais do que um estudo das seis funções em seu
Almagesto, ele da à regra para o cálculo do seno da soma e da diferença de dois
arcos desde que cada um dos senos seja conhecido. Hoje ela é expressa assim:
sem(α±β) =senαcosβ±cosαsenβ.
Os árabes tiveram uma rápida compreensão da necessidade de tábuas de
senos mais detalhadas, por causa da geometria e astronomia. Construíram tabelas
mais precisas. Quem construiu a primeira tabela de seno e tangente foi Al-Hasib
(c.850) com intervalos da primeira até a terceira casa sexagesimal. A intenção era
diminuir os intervalos e melhorar a precisão. Ulugh Beg construiu tábuas das duas
funções no intervalo de 1/60 grau com cinco casas sexagesimais corretas. Já o
astrônomo Al-Kashi utilizou métodos diferentes dos antecedentes, usando sistema
de numeração decimal e considerando o raio igual a 1. No livro “Risala al- watar
wa’l-jaib” de Al-Kashi sobre cordas e senos, ele sugere um procedimento que
envolvia solução por métodos numéricos, de equação de terceiro grau. Al-Kashi
encontrou valor de 60. sen1° correto até nove casas sexagesimais.
355
No decorrer da historia da trigonometria, importantes nomes e descobertas
foram surgindo, como, por exemplo, Tales de Mileto (585 a.C.), que descobriu o
teorema de Tales: “Um feixe de paralelas determinou sobre duas transversais
segmentos proporcionais”.
Pitágoras de Samos nasceu por volta de 580 a.C. Foi um importante
matemático grego que se importou muito com estudos de triângulos retos. Essa é
uma importante definição conhecida como teorema de Pitágoras: Num triangulo
retângulo, o quadrado da hipotenusa (a) é igual à soma dos quadrados dos catetos
(b e c).
Bhaskara Akaria viveu no século XII, ele escreveu um livro de historia da
matemática “Lilavati” que contém vários problemas interessantes, alguns resolvidos
com o teorema de Pitágoras. Tanto na matemática indiana quanto na árabe, foram
encontrados exercícios solucionados com base no teorema de Pitágoras.
Arquimedes nasceu por volta de 287 a.C. em Siracusa, e criou métodos para
solucionar problemas de áreas e volumes. A resolução de um problema de área foi o
motivo da ligação de Arquimedes com a circunferência. Devemos a ele um método
de calcular o valor aproximado de π
(razão entre o comprimento de uma
circunferência e seu diâmetro) utilizando séries. Ele também sabia calcular a área de
círculos. Arquimedes foi considerado o maior matemático da antiguidade.
Erastóstenes viveu por volta de 276-196 a.C., e se destacou nos cálculos
para medir a circunferência da terra, mas tudo que se sabe sobre ele é através de
outros autores. Ele escreveu muitos livros de astronomia, geometria e outros. Os
matemáticos e astrônomos da antiguidade se dedicaram a medir a terra para que
fosse possível medir o tamanho do sol e da lua, mas Erastóstenes foi quem
demonstrou de maneira mais importante.
Hiparco de Nicéia viveu entre 180 e 125 a.C. na Grécia. Influenciado pela
matemática da Babilônia, usufruía a base 60 para realizar suas contas. Ele foi
considerado pai da trigonometria quando construiu uma tabela com os valores das
cordas de uma serie de ângulos de 0° a 180°, o que significou um grande avanço
para astronomia, pois ele havia feito a primeira tabela trigonométrica. Hiparco
também determinou o comprimento da circunferência da terra, porém quem
356
escreveu a obra mais importante da trigonometria na antiguidade, nomeada
síntese matemática foi Ptolomeu de Alexandria, como já mencionado acima.
No Almagesto temos:
Uma tabela mais completa que a de Hiparco, com ângulos de meio em meio
grau, de 0° a 180°;
O uso da base 60, com a circunferência dividida em 360 graus e o raio em 60
partes e frações sexagesimais, não só para expressar ângulos e sim para qualquer
tipo de cálculo, com exceção dos de medida de tempo.
O resultado que passou a ser conhecido como Teorema de Ptolomeu: Se
ABCD é um quadrilátero convexo inscrito num círculo, então a soma dos produtos
dos lados opostos é igual ao produto das diagonais. A partir desse resultado,
operando com as cordas dos arcos, Ptolomeu chegou a um equivalente das
fórmulas de seno da soma e da diferença de dois arcos, isto é sen(a+b) e sen(a-b).
Especialmente a fórmula para a corda da diferença foi usada por ele para a
construção da tabela trigonométrica.
O uso, também usando cordas, do seno do arco metade:
sen²(
π
2
)=
1
(1-cos π )
2
Os hindus também tiveram contribuições de grande importância.No século IV
da nossa era, a Europa Ocidental entrou em crise com as invasões dos bárbaros
germânicos e com a queda do Império Romano. O centro da cultura iniciou um
deslocamento para a Índia, que revolucionou a trigonometria com um conjunto de
textos denominados Siddhanta (sistemas de Astronomia). Logo após, o nome ficou
Surya Siddhanta, que quer dizer Sistemas do Sol. É um texto épico, de
aproximadamente 400 d.C, escrito em versos e em sânscrito. Os hindus diziam que
o autor do texto foi Surya, o deus do Sol.
A importância do Surya, para nós, é que ele abriu novas perspectivas para a
trigonometria por não seguir o mesmo caminho de Ptolomeu, que relacionava as
cordas de um círculo com os ângulos centrais correspondentes. Nas aplicações da
“função” corda, na astronomia, era preciso dobrar o arco antes de usá-lo na tábua de
cordas. Era mais conveniente ter uma tábua na qual o próprio arco fosse à variável
357
independente. No Surya, a relação utilizada era entre a metade da corda e a
metade do ângulo central correspondente, chamada por eles de jiva. Isto possibilitou
a visão de um triângulo retângulo na circunferência.
O .Jiva². Hindu
Os hindus introduziram os métodos de tabulação e aperfeiçoaram,
particularmente os de interpolação quadrática e linear.
Por volta de 500 d.C., o matemático hindu Aryabhata já calculava semi cordas
e também utilizava o sistema decimal, elaborado aproximadamente em 600 d.C. Os
numerais hindus continham nove símbolos e não havia símbolo para o zero.
Quando os hindus introduziram os conceitos de semi corda e de seno,
demonstraram algumas identidades, e encontramos em Varahamihira, no ano 505
d.C., o equivalente verbal de sen²θ + cos² θ = 1
Jogos trigonométricos
Por fazer parte da vida dos jovens, os jogos são uma importante ferramenta
de ensino, e aumentam a capacidade de fixação do conteúdo, também facilitam no
entendimento de regras.
O jogo se ministrado corretamente pode ter a capacidade de ensinar e
aprender se divertindo, também são ótimos recursos para temas mais complicados
como trigonometria, e já existem alguns jogos sobre esse delicado tema, como no
358
Caderno do Mathema. Os jogos estimulam o aluno a usar conceitos estudados
em sala de aula, propriedades e se desenvolver quanto ao conteúdo mesmo sem
que ele perceber. Para que esses jogos possam fazer parte das instituições de
ensino é crucial a atuação do professor.
Valente (1993) destaca, que um dos grandes problemas com jogos é que a
competição pode desviar a atenção da criança do conceito envolvido no jogo.
Caberá ao professor a responsabilidade de mostrar aos alunos que o verdadeiro
objetivo do jogo trabalhado é, atingir o desenvolvimento do conteúdo, e descobrir
suas dificuldades e falhas para tentar corrigi-las de uma maneira mais divertida.
Lara (2004) afirma que jogos bem elaborados podem ser vistos como uma
estratégia de ensino, podendo atingir diferentes objetivos que variam desde o
simples treinamento, até a construção de um determinado conhecimento.
Podemos observar três exemplos de jogos trigonométricos no livro
“Cadernos do Mathema”.
“Os três jogos apresentados no caderno foram planejados de modo a
permitir ao aluno pensar mais sobre medidas em triângulos, bem
como
aprofundar
conceitos
e
procedimentos
trigonométricos”.
(Smole..., 2008, P, 29.).
Os jogos são denominados:
Batalha naval circular: explora a localização de alvos em um circulo orientado,
utilizando como coordenados raios e ângulos.
Batalha trigonométrica: Este jogo, proposto durante e após o estudo da
trigonometria
da
primeira
volta,
pode
auxiliar
os
alunos
a
localizarem
adequadamente pontos no circulo trigonométrico, compreendendo a
relação do
seno, do cosseno e da tangente de ângulos no circulo e favorecendo a memorização
de alguns valores dessas funções trigonométricas.
Trigonometrilha: Este é um jogo de percurso cujo objetivo é possibilitar aos
alunos a utilização de relação simples das funções trigonométricas em arcos
fundamentais, o cálculo aproximado de raízes quadradas, o cálculo de valores
aproximados e a realização de estimativas envolvendo relações trigonométricas.
São opções metodológicas que buscam mudar o panorama das aulas de
trigonometria.
359
REFERÊNCIAS BIBLIOGRÁFICAS
BRITO, A. de J.; MOREY, B. B. Geometria e trigonometria: dificuldades dos
contextos do “mundo experimental” e do computador. 250f. Dissertação (Mestrado)
COSTA, N. M. L., Funções seno e cosseno: uma seqüência de ensino a partir dos
didáticos de Matemática no século XX. In.: Anais do V Seminário Nacional de
em ensino da matemática) – Pontifícia Universidade Católica de São Paulo, São
EVES, Howard. Introdução à História da Matemática – Editora da UniCamp – 3ª
Edição, 2002.
Figuras ufg(universidade federal de Goiás).
FIORENTINI, D. Alguns modos de ver e conceber o ensino da matemática no Brasil.
História da Matemática; Editores Sérgio Nobre e Marcos V. Teixeira. – Rio Claro:
Hogben, Lancelot - Maravilhas da Matemática – Editora Globo – 2ª Edição, Capítulo
VI.
MENDES, I. A. Ensino da Matemática por atividades: uma
aliança entre o construtivismo e a história da matemática.
2001. 283p. Tese (Doutorado em Educação) - Centro de
Ciências Sociais Aplicadas, Universidade Federal do Rio
Grande do Norte, Natal, 2001.
Morey, Bernadete - Geometria e Trigonometria na Índia e nos países árabes abril/2003
NACARATO, Adair Mendes. A definição de seno apresentada nos livros
Paulo, 1997.
Presenças Matemáticas. Natal: Edufrn, 2004. p. 9 - 33.
professores de matemática do ensino fundamental. In: John A. Fossa (org).
360
Revista Zetetiké, Cidade, v. 3, n.4, p. 1–37, 1995.
SBHMat, 2003. (p. 205-213)
SMOLE, Kátia Stocco et al. Cadernos da Mathema. 3. Ed. Porto Alegre: Artmed,
2008. 29 p
i
ii
seno indiano é o comprimento da meia-corda do ângulo central.
(Klaudius Ptolemaios, autor da mais importante obra da trigonometria da Antiguidade, surgida no
século dois de nossa era, em Alexandria, a.Syntaxis Mathemática, composta de treze volumes. Ela
ficou conhecida como Almagesto, que significa em árabe “A maior”, pois os tradutores árabes a
consideravam a maior obra existente na época, em Astronomia).