01) g(1) + g(4) = 1
04) f(g(2)) = 1
16) g(1) + f(–1) = 0
FUNÇÃO COMPOSTA, INVERSA,
1º E 2 GRAU
Obs. No site
www.tudomatematica.com.br
tem questões resolvidas e comentadas
sobre Funções Compostas e Funções do
1º grau,, basta entrar em ENSINO
MÉDIO/QUESTÕES RESOLVIDAS.
01. Considerando a função f ( x ) = x 5 − 6
como
omo bijetora, podemos afirmar que a
inversa de f(x) é....
a) f −1 ( x ) = 6 − x 5
b) f −1 ( x ) = 5 x − 6
c) f −1 ( x ) = 5 x + 6
d) f −1 ( x ) = 5 6 − x
e) f −1 ( x ) = 5 − x − 6
02. Dada a função f ( x ) =
x ≠ 3 , assim...
4x + 3
a) f −1 ( x ) =
x−2
x+3
c) f −1 ( x ) =
x−2
3
x+2
e) f −1 ( x ) =
x−4
02) g(5) = –1
08) g(f(0)) = 0
06. (UEPG/2006)
Em relação à função
f : R → R , definida por f ( x ) = 4 x + 8 e a
sua inversa f −1 ( x ) , assinale o que for correto
x −8
4
02) f(x) é crescente e f −1 ( x ) é decrescente.
01) f −1 ( x ) =
04) Os gráficos de f(x) e f −1 ( x ) são retas
paralelas.
1
08) f (2) ⋅ f −1   = −30
 2
16) Os gráficos
áficos de f(x) e f −1 ( x ) são retas
perpendiculares.
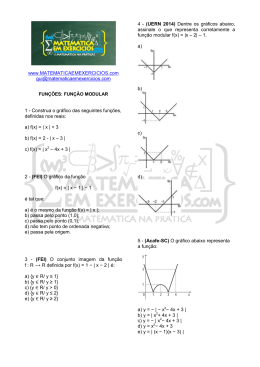
07. (UEM PR/2008) As figuras a seguir
apresentam os gráficos de três funções
f :R → R, p:R →R e q:R → R .
2x + 4
com
x −3
3x + 4
x−2
2x + 3
d) f −1 ( x ) =
x−4
b) f −1 ( x ) =
03. Sejam f, g e h funções reais, tais que
f ( x ) = x − 1 , g(x ) = 2x + 3 e h (x ) = x 2 + 1
. Determine o valor de h (g (f (2))) .
a) 10
b) 12
c) 14
d) 26 e) 40
04. Dadas as funções reais f ( x ) = 3x + 1 e
g ( x ) = 4x − 1 , determine fοg( x ) .
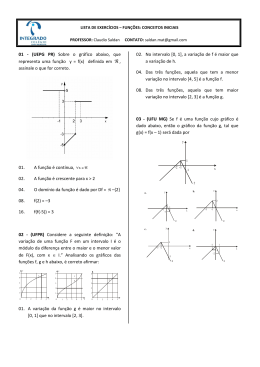
05. (UEPG/2008) O gráfico abaixo representa
a função f(x), definida no intervalo [–1,
[
4].
Considerando que g( x ) = f ( x − 2) , assinale
o que for correto.
Analisando esses gráficos, assinale o que for
correto.
01) (f o q)(0) = 0 .
02) (p o q o f )(2) = 0 .
04) (f − p)(1) = 0 .
08) (p o p)(1) = (f o f )(1) .
16) Se restringirmos o domínio da função f ao
intervalo [0,2], então (p o f −1 )(3) = 3 .
08. (UEPG/2008) Sobre a função real
3
, assinale o que for correto.
c
f (x) =
2−x
01) O gráfico de f(x) intercepta o eixo y em
dois pontos distintos.
02)
Seu
domínio
é
o
conjunto
D = {x ∈ R / x ≠ 2} .
04) Se x ∈ R e x < 2 , então f(x) > 0 .
2x − 3
08) A inversa de f(x) é f −1 ( x ) =
.
x
1
16) f   < 1
 2
09. (UDESC SC) A soma dos coeficientes
a e b da função f ( x ) = ax + b , para que as
afirmações f (0) = 3 e f (1) = 4 sejam
verdadeiras, é:
a)4
b)3
c)2
d)
d)5
e)–4
10. (UEL PR) O gerente de uma agência de
turismo promove passeios de bote para
descer cachoeiras. Ele percebeu que quando
o preço pedido para esse passeio era R$
25,00, o número médio de passageiros por
semana era de 500. Quando o preço era
reduzido para R$ 20,00, o número médio de
fregueses por semana sofria um acréscimo
de 100 passageiros.. Considerando que essa
demanda seja linear, se o preço for reduzido
para R$ 18,00, o número médio de
passageiros esperado por semana será:
a) 360
b) 540 c) 64 d) 700 e) 1360
11. (UEL PR) Os produtos farmacêuticos
devem
especificar
as
dosagens
recomendadas
as para uso de adultos e de
crianças. As fórmulas a seguir são
utilizadas para modificar a dosagem de uso
dos adultos para a dosagem de uso por
crianças (y).
Fórmula A:
Fórmula B:
1
y=
( t + 1) ⋅ a
24
1
y = t ⋅a
21
Onde a denota a dosagem de adulto
ad
em
miligramas e t a idade da criança em anos.
Assinale a alternativa que apresenta a idade
da criança na qual as duas fórmulas
especificam a mesma dosagem.
a) 2 anos.
b) 6 anos. c) 7 anos.
d) 8 anos.
e) 10 anos.
12. Construir o gráfico das funções:
a) y = x 2 − 8 x + 7
a) y = 3 x − 5
13. (Cefet RJ) É dada a função
f(x) = (x – 1) (x – 2) (x – 3).
Para que f(x) < 0, deve-se
se ter:
Resolva
lva as inequações indicadas nas
questões 06 e 07.
2x − 8
14.
≤0
−x+3
15. (− x + 4).(3x − 6) > 0
16. (UCS RS)
Em uma experiência
experiênci
realizada na aula de Biologia, um grupo de
alunos mede o crescimento de uma planta,
em centímetros, todos os dias.
Plotando os pontos (t,a), em que t
corresponde ao tempo em dias, e a
corresponde à altura da planta em
centímetros, os alunos obtiveram a figura
f
a
seguir.
Se essa relação entre tempo e altura da
planta for mantida, estima-se
estima
que, no 34º
dia, a planta tenha, aproximadamente,
a)10 cm. b)6 cm. c)88 cm. d)5 cm. e)7 cm.
17 .(UFPI PI) No conjunto dos números
reais, ℜ , o conjunto-solução
solução da inequação
x −1
< 1 é:
x +1
a) S = {x ∈ ℜ / x < 0}
c) S = {x ∈ ℜ / x > 1}
e) S = {x ∈ ℜ / 0 < x < 3}
b) S = {x ∈ ℜ / − 1 < x < 0}
d) S = {x ∈ ℜ / x > −1}