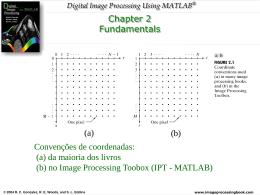
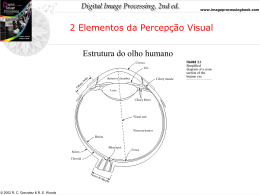
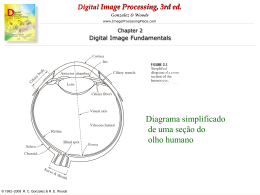
Digital Image Processing Using MATLAB®
Fundamentos
Modelo de imagens
Uma imagem pode ser definida como uma
função de intensidade luminosa 2D, f(x,y), em
que
-- x e y são coordenadas espaciais;
-- amplitude de f na coordenada (x,y) é
valor positivo que fornece a intensidade ou
brilho da imagem naquele ponto.
© 2004 R. C. Gonzalez, R. E. Woods, and S. L. Eddins
www.imageprocessingbook.com
Digital Image Processing Using MATLAB®
Fundamentos
Um modelo simples para a formação da imagem
Um modelo físico para a intensidade de uma cena pode
ser expressa por:
- iluminância (medida em lúmem/m2 ou lux):
quantidade de luz incidente na cena, 0 < i(x,y) < ∞;
- reflectância: quantidade de luz refletida pelos objetos
na cena, 0< r(x,y) <1.
f(x,y) = i(x,y) r(x,y), sendo que
0 < f(x,y) < ∞
© 2004 R. C. Gonzalez, R. E. Woods, and S. L. Eddins
www.imageprocessingbook.com
Digital Image Processing Using MATLAB®
Fundamentos
Alguns exemplos para iluminância:
- em dia claro: 900000 lúmen/m2
- em dia nublado: 10000 lúmen/m2
- sala de escritório: 1000 lúmen/m2
- noite clara (lua cheia): 0.1 lúmen/m2
Alguns exemplos para reflectância:
- neve: 0.93 (reflete 93% da luz incidente)
- parede branca: 0.80
- aço inoxidável: 0 65
- veludo preto: 0.01
© 2004 R. C. Gonzalez, R. E. Woods, and S. L. Eddins
www.imageprocessingbook.com
Digital Image Processing Using MATLAB®
Fundamentos
O significado físico do valor de f(x,y) é
determinado pela fonte de energia.
© 2004 R. C. Gonzalez, R. E. Woods, and S. L. Eddins
www.imageprocessingbook.com
Digital Image Processing Using MATLAB®
Fundamentos
a) Imagens obtidas por raios gama (medicina
nuclear, astronomia)
Cygnus loop:
nuvem de gás
estacionária
superaquecida,
resulta da explosão
de uma estrela na
constelação Cygnus
há 15000 anos.
Bone scan
© 2004 R. C. Gonzalez, R. E. Woods, and S. L. Eddins
www.imageprocessingbook.com
Digital Image Processing Using MATLAB®
Fundamentos
b) Imagens obtidas por Raio X (medicina,
industria, astronomia)
CT da cabeça
Cygnus loop
Placa de circuito
© 2004 R. C. Gonzalez, R. E. Woods, and S. L. Eddins
www.imageprocessingbook.com
Digital Image Processing Using MATLAB®
Fundamentos
c) Imagens obtidas na banda ultravioleta
(litografia, inspeção industrial, microscopia,
imagens biológicas, astronomia)
Cygnus loop
Milho normal
© 2004 R. C. Gonzalez, R. E. Woods, and S. L. Eddins
Milho infectado
www.imageprocessingbook.com
Digital Image Processing Using MATLAB®
Fundamentos
d) Imagens no espectro visível (automação
industrial)
© 2004 R. C. Gonzalez, R. E. Woods, and S. L. Eddins
www.imageprocessingbook.com
Digital Image Processing Using MATLAB®
Fundamentos
e) Imagens obtidas no espectro infravermelho
© 2004 R. C. Gonzalez, R. E. Woods, and S. L. Eddins
www.imageprocessingbook.com
Digital Image Processing Using MATLAB®
Fundamentos
f) Imagens obtidas por micro-ondas (radar)
Montanha no
sudeste do Tibet
© 2004 R. C. Gonzalez, R. E. Woods, and S. L. Eddins
www.imageprocessingbook.com
Digital Image Processing Using MATLAB®
Fundamentos
g) Imagens obtidas na banda de radio (medicina
e astronomia)
MRI do joelho e da coluna
© 2004 R. C. Gonzalez, R. E. Woods, and S. L. Eddins
www.imageprocessingbook.com
Digital Image Processing Using MATLAB®
Fundamentos
gama
Raio - x
ótico
Imagens da Crab Pulsar
infravermelho
© 2004 R. C. Gonzalez, R. E. Woods, and S. L. Eddins
radio
www.imageprocessingbook.com
Digital Image Processing Using MATLAB®
Fundamentos
h) Imagens obtidas por ultra-som (medicina,
exploração geológica)
© 2004 R. C. Gonzalez, R. E. Woods, and S. L. Eddins
www.imageprocessingbook.com
Digital Image Processing Using MATLAB®
Fundamentos
Digitalização da imagem
- Exixtem várias maneiras de adquirir uma
imagem (como vimos);
- A saída da maioria dos sensores gera uma forma
de sinal continuo, cuja amplitude e
comportamento espacial dependem das
características do sensor;
- A imagem digital é obtida pela discretização
dos sinais contínuos para a forma digital.
© 2004 R. C. Gonzalez, R. E. Woods, and S. L. Eddins
www.imageprocessingbook.com
Digital Image Processing Using MATLAB®
Fundamentos
© 2004 R. C. Gonzalez, R. E. Woods, and S. L. Eddins
www.imageprocessingbook.com
Digital Image Processing Using MATLAB®
Fundamentos:
Amostragem e Quantização
A digitalização envolve dois processos:
- Amostragem: consiste em discretizar o domínio
definição da imagem nas direções x e y, gerando uma
matriz de MxN amostras:
- Quantização: consiste em escolher o número L de níveis
de cinza (em imagens monocromáticas) permitidos para
cada imagem, (L = 2k).
Cada elemento f(x,y) desta matriz de amostras é
chamado pixel (pixel element), com
0 <x <M-1 e 0 < y < N-1
© 2004 R. C. Gonzalez, R. E. Woods, and S. L. Eddins
www.imageprocessingbook.com
Digital Image Processing Using MATLAB®
Fundamentos
Representação da Imagem Digital
© 2004 R. C. Gonzalez, R. E. Woods, and S. L. Eddins
www.imageprocessingbook.com
Digital Image Processing Using MATLAB®
Fundamentos
Amostragem
- A digitalização adequada da imagem requer
cuidados para que nenhuma informação
relevante seja perdida no processo de
amostragem;
- Um desses cuidados é a escolha de um
espaçamento entre amostras que garanta a
recuperação da imagem contínua a partir dos
conjunto de valores amostrados (limite de
Nyquist, Δt < 2f0).
© 2004 R. C. Gonzalez, R. E. Woods, and S. L. Eddins
www.imageprocessingbook.com
Digital Image Processing Using MATLAB®
Fundamentos
Na prática, a amostragem é determinada pela matriz
de sensores usada para gerar a imagem
© 2004 R. C. Gonzalez, R. E. Woods, and S. L. Eddins
www.imageprocessingbook.com
Digital Image Processing Using MATLAB®
Fundamentos
Imagem amostrada e quantizada
© 2004 R. C. Gonzalez, R. E. Woods, and S. L. Eddins
www.imageprocessingbook.com
Digital Image Processing Using MATLAB®
Fundamentos
Imagem amostrada e quantizada
O espaço necessário para armazenar uma imagem é
dados por: M x N x k bits ou
N2 x k bits para matrizes quadradas
© 2004 R. C. Gonzalez, R. E. Woods, and S. L. Eddins
www.imageprocessingbook.com
Digital Image Processing Using MATLAB®
Fundamentos
NOTA:
- O tamanho de uma imagem não diz tudo
sobre a sua resolução;
- A qualidade de uma imagem 1024x1024
pixels não pode ser avaliada sem conhecer a
dimensão espacial capturada na imagem.
© 2004 R. C. Gonzalez, R. E. Woods, and S. L. Eddins
www.imageprocessingbook.com
Digital Image Processing Using MATLAB®
Fundamentos
Resolução espacial e de intensidade
Resolução espacial – é uma medida do menor detalhe
discernível em uma imagem;
A resolução espacial pode ser medida por:
- pares de linhas por unidade de distância (100/mm
largura da linha = 0.02 mm);
- pontos (pixels) por unidade de distância – dpi (
usada em industria publicitária e de impressão).
Exemplos:
jornal – 75 dpi, revista – 133 dpi, livros – 2400 dpi
© 2004 R. C. Gonzalez, R. E. Woods, and S. L. Eddins
www.imageprocessingbook.com
Digital Image Processing Using MATLAB®
Fundamentos
Exemplos para resolução espacial
Tamanho da imagem original 2.95 x 2.25 polegadas
3692 x 2812 pixels
© 2004 R. C. Gonzalez, R. E. Woods, and S. L. Eddins
213 x 162 pixels
www.imageprocessingbook.com
Digital Image Processing Using MATLAB®
Fundamentos
Resolução espacial e de intensidade
Resolução de intensidade – refere-se à menor
alteração discernível nos níveis de intensidade;
- em geral o número de níveis de intensidades
é 8 ou 16 bits
© 2004 R. C. Gonzalez, R. E. Woods, and S. L. Eddins
www.imageprocessingbook.com
Digital Image Processing Using MATLAB®
Fundamentos
Resolução espacial e de intensidade
© 2004 R. C. Gonzalez, R. E. Woods, and S. L. Eddins
www.imageprocessingbook.com