Digital Image Processing, 3rd ed.
Gonzalez & Woods
www.ImageProcessingPlace.com
Chapter 2
Digital Image Fundamentals
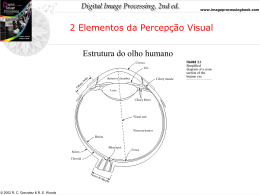
Diagrama simplificado
de uma seção do
olho humano
© 1992–2008 R. C. Gonzalez & R. E. Woods
Digital Image Processing, 3rd ed.
Gonzalez & Woods
www.ImageProcessingPlace.com
Chapter 2
Digital Image Fundamentals
Distribuição de
cones e bastonetes
na retina
© 1992–2008 R. C. Gonzalez & R. E. Woods
Digital Image Processing, 3rd ed.
Gonzalez & Woods
www.ImageProcessingPlace.com
Chapter 2
Digital Image Fundamentals
Representação gráfica do olho vendo uma
palmeira.
O ponto C é o centro óptico da lente.
© 1992–2008 R. C. Gonzalez & R. E. Woods
Digital Image Processing, 3rd ed.
Gonzalez & Woods
www.ImageProcessingPlace.com
Chapter 2
Digital Image Fundamentals
Intervalo da sensação de
brilho subjetivo mostrando
um particular nível de
adaptação.
0,001 a 0,1 mililambert = -3 a -1 mL
© 1992–2008 R. C. Gonzalez & R. E. Woods
scotopic – bastonetes
photopic - cones
Digital Image Processing, 3rd ed.
Gonzalez & Woods
www.ImageProcessingPlace.com
Chapter 2
Digital Image Fundamentals
I = intensidade de fundo
I + DIc = intensidade dentro do círculo
A relação DIc / I é chamada de razão de Weber
© 1992–2008 R. C. Gonzalez & R. E. Woods
Arranjo usado para
caracterizar a
discriminação
de brilho.
Digital Image Processing, 3rd ed.
Gonzalez & Woods
www.ImageProcessingPlace.com
Chapter 2
Digital Image Fundamentals
Razão de Weber
típico como
função da
intensidade.
bastonetes
cones
© 1992–2008 R. C. Gonzalez & R. E. Woods
Digital Image Processing, 3rd ed.
Gonzalez & Woods
www.ImageProcessingPlace.com
Chapter 2
Digital Image Fundamentals
real
percebida
© 1992–2008 R. C. Gonzalez & R. E. Woods
Ilustração do efeito
de banda de Mach.
A intensidade
percebida não é
função simples
da intensidade real.
Digital Image Processing, 3rd ed.
Gonzalez & Woods
www.ImageProcessingPlace.com
Chapter 2
Digital Image Fundamentals
Exemplos de contraste simultâneo. Todos os quadrados
internos tem a mesma intensidade, porém, eles parecem
escurecer a medida que o fundo vai clareando.
© 1992–2008 R. C. Gonzalez & R. E. Woods
Digital Image Processing, 3rd ed.
Gonzalez & Woods
www.ImageProcessingPlace.com
Chapter 2
Digital Image Fundamentals
Algumas ilusões
de óptica bem
conhecidas.
© 1992–2008 R. C. Gonzalez & R. E. Woods
Digital Image Processing, 3rd ed.
Gonzalez & Woods
www.ImageProcessingPlace.com
Chapter 2
Digital Image Fundamentals
Espectro eletromagnético. O espectro visível é mostrado em zoom para
facilitar a explicação, mas o espectro visível é uma porção muito pequena.
© 1992–2008 R. C. Gonzalez & R. E. Woods
Digital Image Processing, 3rd ed.
Gonzalez & Woods
www.ImageProcessingPlace.com
Chapter 2
Digital Image Fundamentals
Representação gráfica de um comprimento de onda.
© 1992–2008 R. C. Gonzalez & R. E. Woods
Digital Image Processing, 3rd ed.
Gonzalez & Woods
www.ImageProcessingPlace.com
Chapter 2
Digital Image Fundamentals
• Modelo de formação da imagem usando iluminação:
• Função 2D de f(x,y)
f(x,y) é positivo e escalar obtido por:
f(x,y) = i(x,y)r(x,y)
onde i(x,y) é a intensidade da luz
0 < i(x,y) < infinito
e r(x,y) é a reflectância
0 < r(x,y) < 1
© 1992–2008 R. C. Gonzalez & R. E. Woods
Digital Image Processing, 3rd ed.
Gonzalez & Woods
www.ImageProcessingPlace.com
Chapter 2
Digital Image Fundamentals
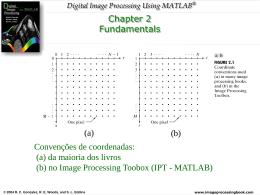
(a)
(b)
Convenções de coordenadas:
(a) da maioria dos livros
(b) no Image Processing Toobox (IPT - MATLAB)
© 1992–2008 R. C. Gonzalez & R. E. Woods
Digital Image Processing, 3rd ed.
Gonzalez & Woods
www.ImageProcessingPlace.com
Chapter 2
Digital Image Fundamentals
(a) sensor pontual de imagem
(b) linha de sensores
(b) matriz de sensores
© 1992–2008 R. C. Gonzalez & R. E. Woods
Digital Image Processing, 3rd ed.
Gonzalez & Woods
www.ImageProcessingPlace.com
Chapter 2
Digital Image Fundamentals
Combinando um sensor
pontual de imagem com
movimento para gerar uma
imagem 2-D.
© 1992–2008 R. C. Gonzalez & R. E. Woods
Digital Image Processing, 3rd ed.
Gonzalez & Woods
www.ImageProcessingPlace.com
Chapter 2
Digital Image Fundamentals
(a) Aquisição de imagem usando uma linha de sensores.
(b) usando uma circunferência de sensores
© 1992–2008 R. C. Gonzalez & R. E. Woods
Digital Image Processing, 3rd ed.
Gonzalez & Woods
www.ImageProcessingPlace.com
Chapter 2
Digital Image Fundamentals
Um exemplo de um processo de aquisição. (a) iluminação
(b) elemento de cena (c) sistema de imageamento
(d) projeção da cena num plano (d) imagem digitalizada.
© 1992–2008 R. C. Gonzalez & R. E. Woods
Digital Image Processing, 3rd ed.
Gonzalez & Woods
www.ImageProcessingPlace.com
Chapter 2
Digital Image Fundamentals
amostragem
(linha A a B
discreta)
© 1992–2008 R. C. Gonzalez & R. E. Woods
quantização
(intensidade
discreta)
Geração de uma imagem
digital.
(a) imagem contínua
(b) uma linha passando de A a B
mostra a intensidade contínua
(c) amostragem e quantização
(d) linha digital passando de A a B
Digital Image Processing, 3rd ed.
Gonzalez & Woods
www.ImageProcessingPlace.com
Chapter 2
Digital Image Fundamentals
(a) imagem contínua projetada numa matriz de sensores
(b) Resultado da imagem amostrada e quantizada
© 1992–2008 R. C. Gonzalez & R. E. Woods
Digital Image Processing, 3rd ed.
Gonzalez & Woods
www.ImageProcessingPlace.com
Chapter 2
Digital Image Fundamentals
(a) Imagem plotada como uma
superfície
(b) Imagem mostrada como uma
matriz de intensidade visual
(c) Imagem mostrada como uma
matriz 2D numérica (0, 0.5 e 1,
representando preto, cinza e branco)
© 1992–2008 R. C. Gonzalez & R. E. Woods
Digital Image Processing, 3rd ed.
Gonzalez & Woods
www.ImageProcessingPlace.com
Chapter 2
Digital Image Fundamentals
Uma imagem exibindo
saturação e ruído.
Saturação é a aproximação
dos níveis acima de um
nível para aquele nível.
Ruído aparece como
uma granulação na textura.
© 1992–2008 R. C. Gonzalez & R. E. Woods
Digital Image Processing, 3rd ed.
Gonzalez & Woods
www.ImageProcessingPlace.com
Chapter 2
Digital Image Fundamentals
Número de bits necessários para
vários valores de N e k.
N = número de pixels na linha
k = número de bits por pixel
© 1992–2008 R. C. Gonzalez & R. E. Woods
Digital Image Processing, 3rd ed.
Gonzalez & Woods
www.ImageProcessingPlace.com
Chapter 2
Digital Image Fundamentals
Efeitos típicos de redução de resolução
espacial.
Imagens mostradas:
(a) 1250 dpi
(b) 300 dpi
(c) 150 dpi
(d) 70 dpi
© 1992–2008 R. C. Gonzalez & R. E. Woods
Digital Image Processing, 3rd ed.
Gonzalez & Woods
www.ImageProcessingPlace.com
Chapter 2
Digital Image Fundamentals
(a) Imagem 452x374 de 256 níveis
(b) a (d) imagens mostradas a 128,
(c) 64, e 32 níveis de cinza, mantendo
a resolução espacial
© 1992–2008 R. C. Gonzalez & R. E. Woods
Digital Image Processing, 3rd ed.
Gonzalez & Woods
www.ImageProcessingPlace.com
Chapter 2
Digital Image Fundamentals
(e) a (h) imagens mostradas
a 16, 8, 4 e 2 níveis de cinza.
© 1992–2008 R. C. Gonzalez & R. E. Woods
Digital Image Processing, 3rd ed.
Gonzalez & Woods
www.ImageProcessingPlace.com
Chapter 2
Digital Image Fundamentals
(a) Imagem com um baixo nível de detalhes
(b) Imagem com nível médio de detalhes
(c) Imagens com uma quantidade relativamente alta de detalhes
© 1992–2008 R. C. Gonzalez & R. E. Woods
Digital Image Processing, 3rd ed.
Gonzalez & Woods
www.ImageProcessingPlace.com
Chapter 2
Digital Image Fundamentals
Curvas de isopreferência para os
3 tipos de imagens, em função de N e k.
A isopreferência foi levantada por
observadores que classificaram as
imagens de acordo com a qualidade
subjetiva.
© 1992–2008 R. C. Gonzalez & R. E. Woods
Digital Image Processing, 3rd ed.
Gonzalez & Woods
www.ImageProcessingPlace.com
Chapter 2
Digital Image Fundamentals
• Interpolação de imagem
•
•
•
•
•
•
•
•
Interpolação é extensivamente usada em tarefas como ampliação (zooming),
encolhimento (shrinking), rotação e correções geométricas.
Interpolação é o processo de usar dados conhecidos para estimar valores em locais
desconhecidos.
Supomos que uma imagem de 500x500 pixels deve ser ampliado 1,5 vezes para
750x750 pixels.
Uma forma de visualizar essa ampliação é criar uma grade imaginária 750x750
com o mesmo espaçamento da imagem original e então encolher essa grade até que
ela se enquadre sobre a imagem original.
Obviamente, o espaçamento na grade encolhida de 750x750 pixels é menor que na
imagem original.
Para realizar a atribuição de nível de intensidade para qualquer ponto na grade de
750x750, olha-se o pixel mais próximo na imagem original e atribui a sua
intensidade para o novo pixel.
Quando tivermos realizada a atribuição de todos os 750x750 pixels expande-se a
grade para o tamanho original obtendo a imagem ampliada.
O método acima é chamado de interpolação de vizinho mais próximo (nearest
neighbor interpolation).
© 1992–2008 R. C. Gonzalez & R. E. Woods
Digital Image Processing, 3rd ed.
Gonzalez & Woods
www.ImageProcessingPlace.com
Chapter 2
Digital Image Fundamentals
• O procedimento do vizinho mais próximo é simples mas existe uma
tendência a produzir efeitos indesejáveis, como uma distorção severa em
arestas (edges) retas. Por isso o método não é muito usado.
• Uma abordagem mais adequada é a interpolação bilinear, em que usamos os
quatro vizinhos mais próximos para estimar a intensidade numa dada
posição.
• Seja (x,y) as coordenadas da posição considerada, e seja v(x,y) o valor da
intensidade.
• Para a interpolação bilinear, o valor atribuído é obtido usando a equação
v(x,y) = ax + by + cxy +d
(eq. 2.4-6)
onde os quatro coeficientes são determinados de quatro equações em quatro
incógnitas que podem ser escritas usando os quatro vizinhos mais próximos
do ponto (x,y).
• O resultado é melhor que a interpolação de vizinho mais próximo, com um
pequeno incremento no custo computacional.
© 1992–2008 R. C. Gonzalez & R. E. Woods
Digital Image Processing, 3rd ed.
Gonzalez & Woods
www.ImageProcessingPlace.com
Chapter 2
Digital Image Fundamentals
•
•
O próximo nível de complexidade é a interpolação bicúbica, que envolve dezesseis vizinhos
mais próximos de um ponto.
O valor da intensidade atribuído ao ponto (x,y) é obtido usando a equação
3
3
v( x, y)   aij xi y j
(eq. 2.4-7)
i 0 j 0
•
•
•
onde os dezesseis coeficientes são determinados de dezesseis equações em dezesseis
incógnitas que podem ser escritas usando os dezesseis vizinhos mais próximos do ponto (x,y).
Observa-se que a eq. 2.4-7 reduz em forma para eq. 2.4-6 se os limites de ambos os
somatórios são 0 e 1.
Geralmente a interpolação bicúbica realiza um papel melhor de preservar detalhes que a
interpolação bilinear.
Interpolação bicúbica é o padrão usado em programas comerciais como Adobe Photoshop e
Corel Photopaint.
© 1992–2008 R. C. Gonzalez & R. E. Woods
Digital Image Processing, 3rd ed.
Gonzalez & Woods
www.ImageProcessingPlace.com
Chapter 2
Digital Image Fundamentals
(a) imagem reduzida a 72 dpi e
expandida de volta a 3692x 2812
usando interpolação de vizinho mais
próximo. Essa figura é a mesma da
Fig. 2.20 (d).
(b) Imagem encolhida e expandida
usando interpolação bilinear.
(c) Como em (b) mas usando
interpolação bicúbica
(d) a (f) mesma sequência, mas
encolhendo para 150 dpi ao invés
de 72 dpi.
© 1992–2008 R. C. Gonzalez & R. E. Woods
Digital Image Processing, 3rd ed.
Gonzalez & Woods
www.ImageProcessingPlace.com
Chapter 2
Digital Image Fundamentals
• Relações entre pixels
– Um pixel p numa coordenada (x,y) tem quatro vizinhos cujas
coordenadas são:
– (x+1,y), (x-1,y),(x,y+1) e (x,y-1)
– Esse conjunto de pixels é chamado de vizinhança-4 de p, denotado por
N4(p)
– Os quatro vizinhos na diagonal de p tem coordenadas:
– (x+1,y+1),(x+1,y-1),(x-1,y+1) e (x-1,y-1)
– E são denotados por ND(p)
– O conjunto de N4(p) e ND(p) é chamado de vizinhança-8, e denotado
por N8(p).
© 1992–2008 R. C. Gonzalez & R. E. Woods
Digital Image Processing, 3rd ed.
Gonzalez & Woods
www.ImageProcessingPlace.com
Chapter 2
Digital Image Fundamentals
• Adjacência, conectividade, regiões e contornos
– Seja V o conjunto de valores de intensidade usado para a definição de
adjacência.
– Adjacência-4: dois pixels p e q, com valores no conjunto V, tem
adjacência-4 se q está no conjunto N4(p).
– Adjacência-8: dois pixels p e q, com valores no conjunto V, tem
adjacência-8 se q está no conjunto N8(p).
– Adjacência-m (mista): dois pixels p e q, com valores no conjunto V,
tem adjacência-m se q está no conjunto N4(p), ou q está em ND(p) e se
a intersecção do conjunto N4(p) e N4 (q) não tem nenhum pixel com
valor em V.
© 1992–2008 R. C. Gonzalez & R. E. Woods
Digital Image Processing, 3rd ed.
Gonzalez & Woods
www.ImageProcessingPlace.com
Chapter 2
Digital Image Fundamentals
Um caminho digital ou curva digital de um pixel p com coordenadas (x,y)
a um pixel q com coordenadas (s,t) é uma sequência de pixels distintos
com coordenadas
(x0,y0), (x1,y1), ..., (xn, yn)
onde (x0,y0) = (x,y), (xn,yn) = (s,t) e pixels (xi, yi) e (xi-1, yi-1) são
adjacentes para 1  i  n .
Neste caso, n é o comprimento do caminho.
Se (x0,y0) = (xn, yn), o caminho é fechado.
Pode-se definir caminho-4, caminho-8, ou caminho-m, dependendo do tipo
de adjacência especificado.
© 1992–2008 R. C. Gonzalez & R. E. Woods
Digital Image Processing, 3rd ed.
Gonzalez & Woods
www.ImageProcessingPlace.com
Chapter 2
Digital Image Fundamentals
•
•
Seja S um subconjunto de pixels de uma imagem.
Dois pixels p e q são ditos conectados em S se existe um caminho entre
eles consistindo inteiramente de pixels em S.
• Para qualquer pixel p em S, o conjunto de pixels que são conectados a ele
em S é chamado um componente conectado de S. Se existe apenas um
componente conectado, então S é chamado de conjunto conectado.
• Seja R um subconjunto de pixels numa imagem. Chamamos R de uma região
da imagem se R é um conjunto conectado.
• Duas regiões Ri e Rj são chamados adjacentes se a sua união forma
um conjunto conectado.
• Regiões que não são adjacentes são ditos disjuntos.
• Existem adjacências-4, -8 quando se refere a regiões.
© 1992–2008 R. C. Gonzalez & R. E. Woods
Digital Image Processing, 3rd ed.
Gonzalez & Woods
www.ImageProcessingPlace.com
Chapter 2
Digital Image Fundamentals
• Supõe-se que uma imagem contenha K regiões disjuntas, Rk, k = 1,2,...,K,
nenhuma delas tocando a borda da imagem.
• Seja Ru a união de todas as K regiões, e seja (Ru)c o seu complemento (o
complemento de um conjunto S é um conjunto de pontos que não
pertencem a S).
• Chama-se todos os pontos em Ru de foreground, e todos os pontos em
(Ru)c de background da imagem.
• O contorno (boundary) ou borda (border) de uma região R é o conjunto de
pontos que são adjacentes a pontos do complemento de R. Ou seja, a borda
de uma região é o conjunto de pixels na região que tem pelo menos um
vizinho background.
© 1992–2008 R. C. Gonzalez & R. E. Woods
Digital Image Processing, 3rd ed.
Gonzalez & Woods
www.ImageProcessingPlace.com
Chapter 2
Digital Image Fundamentals
• A definição anterior se refere à borda interna (inner border) da região para
distinguir da borda externa (outer border), que é a borda correspondente no
background.
• Muitos algoritmos são formulados em função do outer border para garantir
que o resultado forme um caminho fechado.
• Por exemplo, na Fig. 2.25 (f) a borda interna da região com valores 1 é a
própria região. Essa borda não satisfaz a definição de um caminho fechado.
• Por outro lado, a borda externa da região forma um caminho fechado em
torno da região.
• Se R for uma imagem inteira, então a sua borda é definida como o conjunto
de pixels da primeira e última linhas e colunas da imagem.
• A definição acima é necessária porque uma imagem não tem vizinhos além
da borda.
© 1992–2008 R. C. Gonzalez & R. E. Woods
Digital Image Processing, 3rd ed.
Gonzalez & Woods
www.ImageProcessingPlace.com
Chapter 2
Digital Image Fundamentals
• O conceito de edge (aresta) é diferente de borda (border ou boundary).
• A borda de uma região finita forma um caminho fechado.
• Edges são formados de pixels com valores derivativos que excedem um
limiar.
• Assim um edge é baseado numa medida de descontinuidade do nível de
intensidade.
• Quando a imagem é binária, pode coincidir um edge e borda de uma região.
© 1992–2008 R. C. Gonzalez & R. E. Woods
Digital Image Processing, 3rd ed.
Gonzalez & Woods
www.ImageProcessingPlace.com
Chapter 2
Digital Image Fundamentals
(a) Um arranjo de pixels
(b) Pixels que são adjacente-8
(adjacências mostradas em linhas
tracejadas)
(c) adjacência-m
(d) Duas regiões que são adjacentes
se usar adjacência-8
(e) O ponto circulado é parte de um
contorno de pixels com valor 1 somente
se adjacência-8 entre a região e o
background é usada.
(f) O contorno interno da região com
valor 1 não forma um caminho fechado,
mas o seu contorno externo sim.
© 1992–2008 R. C. Gonzalez & R. E. Woods
Digital Image Processing, 3rd ed.
Gonzalez & Woods
www.ImageProcessingPlace.com
Chapter 2
Digital Image Fundamentals
•
Medidas de distância
– Para pixels p, q e z com coordenadas
(x,y), (s,t) e (v,w), respectivamente, D
é uma função distância ou métrica se:
– (a)
( D( p, q)  0 iff
– (b) D( p, q)  0
– (c) D( p, q)  D(q, p), e
D( p, z)  D( p, q)  D(q, z ).
– A distância euclidiana entre p e q é
definida por

© 1992–2008 R. C. Gonzalez & R. E. Woods

1
2 2
De ( p, q)  x  s    y  t 
2
p  q),
Digital Image Processing, 3rd ed.
Gonzalez & Woods
www.ImageProcessingPlace.com
Chapter 2
Digital Image Fundamentals
•
A distância D4 (city-block distance)
entre p e q é definida por:
D4 ( p, q) | x  s |  | y  t |
•
A distância D8 (chessboard distance)
é definida por:
D8 ( p, q)  max(|x  s |, | y  t |)
© 1992–2008 R. C. Gonzalez & R. E. Woods
2
2 1 2
2 1 0 1 2
Posição de
2 1 2
2
(x,y)
Posição de
(x,y) 2
2
2
2
2
Distância na
posição
(s,t)
Distância na
2
1
1
1
2
2
1
0
1
2
2
1
1
1
2
2
2
2
2
2
posição
(s,t)
Digital Image Processing, 3rd ed.
Gonzalez & Woods
www.ImageProcessingPlace.com
Chapter 2
Digital Image Fundamentals
• Operações array versus matrix:
– Sejam
 a11 a12 
a

 21 a22 
e
b11 b12 
b b 
 21 22 
– Array product:
 a11 a12 
a

a
 21 22 
b11 b12   a11b11 a12b12 
b b   a b

a
b
 21 22   21 21 22 22 
– Matrix product:
 a11 a12 
a

a
 21 22 
© 1992–2008 R. C. Gonzalez & R. E. Woods
b11 b12   a11b11  a12b21 a11b12  a12b22 
b b   a b  a b

a
b

a
b
 21 22   21 11 22 21 21 12 22 22 
Digital Image Processing, 3rd ed.
Gonzalez & Woods
www.ImageProcessingPlace.com
Chapter 2
Digital Image Fundamentals
• Operações lineares versus não-lineares.
– Considerando-se um operador genérico H, que produz uma imagem de
saída g(x,y), para uma dada imagem de entrada f(x,y):
H [ f(x,y) ] = g (x,y)
– H é um operador linear se



H ai f i ( x, y )  a j f j ( x, y )  ai H  f i ( x, y )  a j H f j ( x, y )

 ai g i ( x, y )  a j g j ( x, y )
onde ai , aj , fi(x,y) e fj(x,y) são
constantes arbitrárias e imagens de mesmo tamanho, respectivamente.
Aditividade – a saída de uma operação linear da soma de duas entradas
é a mesma que realizar a operação linear individualmente para as entradas
e somar o resultado.
Homogeneidade – a saída de uma operação sobre a entrada multiplicada por
uma constante é igual a saída da operação sobre a entrada original multiplicada
pela constante.
© 1992–2008 R. C. Gonzalez & R. E. Woods
Digital Image Processing, 3rd ed.
Gonzalez & Woods
www.ImageProcessingPlace.com
Chapter 2
Digital Image Fundamentals
•
Exemplo. Seja H operador soma S.
 a f ( x, y)  a
1 1
f ( x, y )   a1 f1 ( x, y )   a2 f 2 ( x, y )
2 2
 a1  f1 ( x, y )  a2  f 2 ( x, y )
 a1 g1 ( x, y )  a2 g 2 ( x, y )
Sejam
0 2
f1 ( x, y)  

2 3
e
6 5
f 2 ( x, y)  

4 7 
Verificar se H é linear, usando as matrizes acima e
adotando valores para as constantes a1 e a2 .
© 1992–2008 R. C. Gonzalez & R. E. Woods
Digital Image Processing, 3rd ed.
Gonzalez & Woods
www.ImageProcessingPlace.com
Chapter 2
Digital Image Fundamentals
Sejam
0 2
f1 ( x, y)  

2 3
e
6 5
f 2 ( x, y)  

4 7 
a1 = 1 e a2 = -1
Seja o operador max que obtem o máximo elemento da matriz.
 0 2
   6  3 
6 5  
max((1) 
  (1) 4 7   max 2  4   2
2
3




 

  0 2 
 6 5  
(1) max
  (1) max
  3  (1)7  4


  2 3 
 4 7  
Portanto max é um operador não-linear.
© 1992–2008 R. C. Gonzalez & R. E. Woods
Digital Image Processing, 3rd ed.
Gonzalez & Woods
www.ImageProcessingPlace.com
Chapter 2
Digital Image Fundamentals
• Operações lineares são excepcionalmente importantes para processamento
de imagens digitais.
• Sistemas não-lineares tem um escopo limitado de aplicações, porém,
existem vários casos de aplicações em que o desempenho é melhor que os
sistemas lineares.
© 1992–2008 R. C. Gonzalez & R. E. Woods
Digital Image Processing, 3rd ed.
Gonzalez & Woods
www.ImageProcessingPlace.com
Chapter 2
Digital Image Fundamentals
•
Operações aritméticas sobre imagens:
s(x,y) = f(x,y) + g(x,y)
d(x,y) = f(x,y) – g(x,y)
p(x,y) = f(x,y) x g(x,y)
v(x,y) = f(x,y) g(x,y)

Onde as operações são feitas entre os pixels correspondentes em f e g para
x = 0,1,2,... M-1 e y=0,1,2,...,N-1,
onde M e N são os tamanhos de linha e coluna das imagens.
© 1992–2008 R. C. Gonzalez & R. E. Woods
Digital Image Processing, 3rd ed.
Gonzalez & Woods
www.ImageProcessingPlace.com
Chapter 2
Digital Image Fundamentals
• Exemplo: seja g(x,y) uma imagem corrompida formada com a adição de
ruído h(x,y) a uma imagem sem ruído f(x,y):
g(x,y) = f(x,y) + h(x,y)
onde presume-se que a cada par de coordenadas (x,y) o ruído não esteja
correlacionado e tem média zero.
• O objetivo do procedimento seguinte é reduzir o ruído somando um conjunto de
imagens ruidosas, {gi(x,y)}, e dividindo o resultado pelo número de imagens
somadas. Essa é uma técnica frequentemente usada para o melhoramento de
imagens.
1
g ( x, y ) 
K


K
 g ( x, y )
i 1
i
E g ( x, y)  f ( x, y)
•
Na prática as imagens gi(x,y) devem ser alinhadas (registradas) para evitar a
introdução de borramento (blurring).
© 1992–2008 R. C. Gonzalez & R. E. Woods
Digital Image Processing, 3rd ed.
Gonzalez & Woods
www.ImageProcessingPlace.com
Chapter 2
Digital Image Fundamentals
(a) Imagem da galáxia
corrompida por ruído
Gaussiano aditivo.
(b) – (f) Resultado da
média com 5, 10, 20, 50 e
100 imagens ruidosas,
respectivamente.
© 1992–2008 R. C. Gonzalez & R. E. Woods
Digital Image Processing, 3rd ed.
Gonzalez & Woods
www.ImageProcessingPlace.com
Chapter 2
Digital Image Fundamentals
• Aplicação frequente de subtração de imagens é no melhoramento das
diferenças em imagens.
• Exemplo 1: imagem infravermelho da área de Washington, D.C.
(Fig. 2.27)
• Exemplo 2: radiografia no modo máscara.
g(x,y) = f(x,y) – h(x,y),
onde h(x,y) é uma máscara, em imagem de raios-X de uma região do corpo do
paciente, capturado por uma câmera de TV intensificada. A imagem ativa
de raios-X é denotada f(x,y).
(Fig. 2.28)
© 1992–2008 R. C. Gonzalez & R. E. Woods
Digital Image Processing, 3rd ed.
Gonzalez & Woods
www.ImageProcessingPlace.com
Chapter 2
Digital Image Fundamentals
(a) Imagem infravermelho da área de Washington, D.C.
(b) Imagem obtida zerando o bit menos significativo de todos os pixels em (a)
(c) Diferência das duas imagens, escalado para o intervalo [0,255].
© 1992–2008 R. C. Gonzalez & R. E. Woods
Digital Image Processing, 3rd ed.
Gonzalez & Woods
www.ImageProcessingPlace.com
Chapter 2
Digital Image Fundamentals
Angiografia de subtração
digital.
(a) Imagem máscara
(b) Imagem ativa
(c) Diferença entre (a) e (b)
(d) Imagem da diferença
melhorada
© 1992–2008 R. C. Gonzalez & R. E. Woods
Digital Image Processing, 3rd ed.
Gonzalez & Woods
www.ImageProcessingPlace.com
Chapter 2
Digital Image Fundamentals
• Exemplo de multiplicação (e divisão) de imagens é na correção de
sombreamento.
g(x,y) = f(x,y)h(x,y)
f(x,y) é a imagem perfeita
g(x,y) é a imagem sombreada
h(x,y) é o padrão de sombreamento
Conhecendo-se g(x,y) e h(x,y), é possível obter a imagem f(x,y) multiplicando
g(x,y) pelo inverso de h(x,y).
© 1992–2008 R. C. Gonzalez & R. E. Woods
Digital Image Processing, 3rd ed.
Gonzalez & Woods
www.ImageProcessingPlace.com
Chapter 2
Digital Image Fundamentals
Correção de sombreamento. (a) imagem SEM sombreada de um
filamento de tungstênio e suporte, aumentado aprox. 130 vezes.
(b) padrão de sombremento. (c) produto de (a) pelo recíproco de (b)
© 1992–2008 R. C. Gonzalez & R. E. Woods
Digital Image Processing, 3rd ed.
Gonzalez & Woods
www.ImageProcessingPlace.com
Chapter 2
Digital Image Fundamentals
• Uma outra aplicação de multiplicação de imagens é no mascaramento da
região de interesse (ROI – Region Of Interest).
• A imagem a ser multiplicada é uma máscara que tem valor 1 na ROI e valor
0 em outras posições.
© 1992–2008 R. C. Gonzalez & R. E. Woods
Digital Image Processing, 3rd ed.
Gonzalez & Woods
www.ImageProcessingPlace.com
Chapter 2
Digital Image Fundamentals
(a) Imagem de raios-X digital. (b) máscaras de ROI (Region Of Interest)
para isolar os dentes. (c) produto entre (a) e (b).
© 1992–2008 R. C. Gonzalez & R. E. Woods
Digital Image Processing, 3rd ed.
Gonzalez & Woods
www.ImageProcessingPlace.com
Chapter 2
Digital Image Fundamentals
•
Operações lógicas e de conjunto
•
Operações básicas de conjuntos. Seja A um conjunto composto de pares
ordenados de números reais. Se a = (a1,a2) é um elemento de A, escrevemos
a A
Se a não é um elemento de A escrevemos
a A
O conjunto sem nenhum elemento é chamado conjunto vazio e é denotado por  .
Um conjunto é especificado usando duas chaves {.}, por exemplo:
C  w | w  d , d  D
onde o conjunto C é o conjunto de elementos w tais que w são formados
multiplicando cada um dos elementos do conjunto D por -1.
© 1992–2008 R. C. Gonzalez & R. E. Woods
Digital Image Processing, 3rd ed.
Gonzalez & Woods
www.ImageProcessingPlace.com
Chapter 2
Digital Image Fundamentals
•
•
Uma forma dos conjuntos serem usados em processamento de imagens é
permitir que os elementos dos conjuntos serem coordenadas dos pixels que
representam regiões de uma imagem.
Se cada elemento de A é também elemento de B, então A é dito ser um
subconjunto de B, denotado por
A B
•
A união de dois conjuntos A e B, denotada por
C  A B
•
é o conjunto de elementos pertencentes a A, B ou ambos.
Similarmente, a interseção de dois conjuntos A e B, denotada por
D  A B
é o conjunto de elementos pertencentes a ambos A e B. Dois conjuntos A e B
são ditos disjuntos ou mutuamente exclusivos se eles não tem nenhum
elemento em comum, caso em que
A B  
© 1992–2008 R. C. Gonzalez & R. E. Woods
Digital Image Processing, 3rd ed.
Gonzalez & Woods
www.ImageProcessingPlace.com
Chapter 2
Digital Image Fundamentals
•
•
O conjunto universo é o conjunto de todos os elementos numa dada aplicação.
O complemento de um conjunto A é o conjunto de elementos que não estão em A:
Ac  w | w  A
•
A diferença de dois conjuntos A e B, denotada A – B é definida por
A  B  w | w  A, w  B  A  Bc
•
Vemos que este é um conjunto de elementos que pertencem a A mas não pertencem a B.
Podemos definir Ac em termos de U e estabelecer a equação
Ac = U – A.
© 1992–2008 R. C. Gonzalez & R. E. Woods
Digital Image Processing, 3rd ed.
Gonzalez & Woods
www.ImageProcessingPlace.com
Chapter 2
Digital Image Fundamentals
(a) Dois conjuntos de coordenadas, A e B no espaço 2D.
(b) União de A e B
(c) Intersecção de A e B
(d) O complemento de A
(e) A diferença entre A e B.
As áreas sombreadas representam
os elementos da operação resultante.
© 1992–2008 R. C. Gonzalez & R. E. Woods
Digital Image Processing, 3rd ed.
Gonzalez & Woods
www.ImageProcessingPlace.com
Chapter 2
Digital Image Fundamentals
A união de dois conjuntos A e B em escala de cinza
pode ser definida como o conjunto
A  B  max(a, b) | a  A, b  B
© 1992–2008 R. C. Gonzalez & R. E. Woods
Operações de conjunto.
(a) Imagem original
(b) Imagem negativa
usando complementação
(c) União de (a) e uma
imagem constante
Digital Image Processing, 3rd ed.
Gonzalez & Woods
www.ImageProcessingPlace.com
Chapter 2
Digital Image Fundamentals
Operações lógicas envolvendo
foreground (branco).
As linhas tracejadas são
mostradas para referência
e não fazem parte do resultado
© 1992–2008 R. C. Gonzalez & R. E. Woods
Digital Image Processing, 3rd ed.
Gonzalez & Woods
www.ImageProcessingPlace.com
Chapter 2
Digital Image Fundamentals
Operações sobre pixels individuais
(single-pixel operations)
S = T(z)
Função de transformação de
intensidade usada para obter o
negativo de uma imagem de 8 bits.
As setas tracejadas mostram a
transformação de um valor de
intensidade de entrada arbitrária z0
para um valor de saída correspondente s0.
© 1992–2008 R. C. Gonzalez & R. E. Woods
Digital Image Processing, 3rd ed.
Gonzalez & Woods
www.ImageProcessingPlace.com
Chapter 2
Digital Image Fundamentals
Operações sobre a vizinhança
Média local usando
processamento de
vizinhança.
O procedimento é
ilustrado em (a) e (b)
para uma vizinhança
retangular.
(c) o angiograma aórtico
(d) resultado usando
Eq. 2.6-21, com m=n=41.
Tamanho das imagens
790x686 pixels.
g ( x, y) 
© 1992–2008 R. C. Gonzalez & R. E. Woods
1
 f ( r , c)
m n ( r ,c )S xy
(eq.2.6-21)
Digital Image Processing, 3rd ed.
Gonzalez & Woods
www.ImageProcessingPlace.com
Chapter 2
Digital Image Fundamentals
• Transformações espaciais geométricas
•
•
•
•
•
Transformações geométricas modificam a relação espacial entre os pixels. Em termos
de processamento de imagens digitais a transformação geométrica consiste de duas
operações básicas: (1) transformação espacial de coordenadas e (2) interpolação de
intensidade que atribui valores de intensidade para pixels transformados.
A transformação de coordenadas pode ser expressa por
(x,y) = T {(v,w)}
onde (v,w) são as coordenadas do pixel na imagem original e (x,y) são as coordenadas
do pixel correspondente na imagem transformada.
Uma das transformações mais comum é chamada transformada afim, que tem a forma:
t11 t12
x y 1  v w 1T  v w 1t21 t22
t31 t32
© 1992–2008 R. C. Gonzalez & R. E. Woods
0
0
1
(eq. 2.6-23)
Digital Image Processing, 3rd ed.
Gonzalez & Woods
www.ImageProcessingPlace.com
Chapter 2
Digital Image Fundamentals
Transformadas afins
baseadas na
eq. 2.6-23
© 1992–2008 R. C. Gonzalez & R. E. Woods
Digital Image Processing, 3rd ed.
Gonzalez & Woods
www.ImageProcessingPlace.com
Chapter 2
Digital Image Fundamentals
(a) Imagem de 300 dpi da letra T.
(b) Imagem rotacionada 210 sentido horário usando interpolação
de vizinho mais próximo
(c) Imagem rotacionada 210 usando interpolação bilinear
(d) Imagem rotacionada 210 usando interpolação bicúbica.
a seção ampliada mostra detalhes da borda para as três abordagens
© 1992–2008 R. C. Gonzalez & R. E. Woods
Digital Image Processing, 3rd ed.
Gonzalez & Woods
www.ImageProcessingPlace.com
Chapter 2
Digital Image Fundamentals
• Registro de imagens (alinhamento)
•
•
•
•
•
Registro de imagem é uma aplicação importante usada para alinhar dois ou mais
imagens da mesma cena.
No registro de imagem dispomos das imagens de entrada e de saída, mas a
transformação específica que produziu a imagem de saída a partir da imagem de
entrada é desconhecida.
O problema é então estimar a função de transformação e então usá-la para registrar
(alinhar) as duas imagens.
A imagem de entrada é a imagem que queremos alinhar, e a imagem de referência é
aquela usada para alinhar a imagem de entrada.
Por exemplo, queremos alinhar duas ou mais imagens obtidas aproximadamente ao
mesmo tempo, mas usando diferentes sistemas de imageamento, como MRI, PET. Ou
talvez, as imagens foram tomadas em diferentes tempos usando um mesmo
instrumento. Em ambos os casos, combinação de imagens para realizar análise
quantitativa e comparações entre elas requer compensação das distorsões geométricas
causadas por diferenças de ângulo de visão, distância e orientação, resolução de
sensor, deslocamento na posição de objetos, e outros fatores.
© 1992–2008 R. C. Gonzalez & R. E. Woods
Digital Image Processing, 3rd ed.
Gonzalez & Woods
www.ImageProcessingPlace.com
Chapter 2
Digital Image Fundamentals
•
•
•
•
Uma das principais abordagens é usar pontos de controle (tie points), que são pontos
correspondentes conhecidos precisamente na imagem de entrada e na imagem de referência.
Existem numerosas formas de selecionar os pontos de controle.
Em algumas aplicações, sistemas de imageamento tem artefatos físicos embutidos nos
sensores. Eles produzem um conjunto de pontos conhecidos nas imagens capturadas, que
podem ser usadas como guias para estabelecer os pontos de controle.
Para estimar a função de transformação, supomos que tenhamos um conjunto de quatro
pontos de controle, na imagem de entrada e na imagem de referência. Um modelo simples
baseado na aproximação bilinear é dada por
e
x  c1v  c2 w  c3vw  c4
y  c5v  c6 w  c7vw  c8
onde durante a fase de estimação, (v,w) e (x,y) são as coordenadas dos pontos de controle na
imagem de entrada e na imagem de referência, respectivamente.
• Se tivermos quatro pares de pontos de controle correspondentes em duas imagens, podemos
escrever oito equações usando as equaçãoes acima, e obtemos os 8 coeficientes
desconhecidos.
© 1992–2008 R. C. Gonzalez & R. E. Woods
Digital Image Processing, 3rd ed.
Gonzalez & Woods
www.ImageProcessingPlace.com
Chapter 2
Digital Image Fundamentals
Registro de imagens.
(a) Imagem de referência
(b) Imagem de entrada
(distorcida geometrica/)
(c) Imagem registrada
(d) Diferença entre (a) e (c)
© 1992–2008 R. C. Gonzalez & R. E. Woods
Digital Image Processing, 3rd ed.
Gonzalez & Woods
www.ImageProcessingPlace.com
Chapter 2
Digital Image Fundamentals
•
•
Operações vetoriais e matriciais
O processamento de imagens multiespectrais é uma área típica em que operaçõese
vetoriais e matriciais são usadas. Por exemplo, cada pixel de uma imagem RGB tem 3
componentes, que podem ser organizados na forma de um vetor coluna
 z1 
z   z 2 
 z3 
onde z1 é a intensidade do pixel na imagem vermelha, e os dois outros elementos são
os pixels nas imagens verde e azul, respectivamente. Assim, uma imagem RGB de
tamanho MxN pode ser representada por 3 imagens componentes, ou por um total de
MN vetores 3D.
© 1992–2008 R. C. Gonzalez & R. E. Woods
Digital Image Processing, 3rd ed.
Gonzalez & Woods
www.ImageProcessingPlace.com
Chapter 2
Digital Image Fundamentals
•
A distância euclidiana D entre um vetor de pixel z e um ponto arbitrário a num espaço ndimensional é definida como o produto vetorial:

D(z ,a)  (z  a) (z  a)

•
T

1
2
 ( z1  a1 )  ( z2  a2 )  ...  ( zn  an )
2
2

1
2 2
Uma transformação linear sobre um vetor de pixel é dada por
w  A(z  a)
onde A é uma matriz de tamanho mxn e z e a são vetores coluna de tamanho n x1.
Uma outra aplicação das operações vetoriais e matriciais é a representação de uma imagem MxN
como um vetor de dimensão MNx1 fazendo com que a primeira linha da imagem seja os
primeiros N elementos do vetor, a segunda linha, os próximos N elementos, e assim por diante.
Com imagens formadas dessa forma pode-e usar a notação
g  Hf  n
onde f é um vetor MNx1 representando a imagem de entrada, n é um vetor MNx1 representando
o padrão de ruído MxN e g é um vetor MNx1 repreentando a imagem processada, e H é uma
matriz MNxMN representando um processo linear aplicado à imagem de entrada.
© 1992–2008 R. C. Gonzalez & R. E. Woods
Digital Image Processing, 3rd ed.
Gonzalez & Woods
www.ImageProcessingPlace.com
Chapter 2
Digital Image Fundamentals
Formação de um vetor
com valores de pixels
em 3 imagens componentes
RGB.
© 1992–2008 R. C. Gonzalez & R. E. Woods
Digital Image Processing, 3rd ed.
Gonzalez & Woods
www.ImageProcessingPlace.com
Chapter 2
Digital Image Fundamentals
•
•
Transformada de imagens
Em alguns casos as tarefas de processamento de imagens são melhores formuladas
transformando as imagens de entrada, e aplicando a transformada inversa para
retornar ao domínio espacial. Uma importante classe de transformada linear 2D,
denotada T(u,v) pode ser expressa na forma geral
M  2 N 1
(eq.2.6-30)
T (u, v) 
 f ( x, y)r ( x, y, u, v)
x 0 y 0
onde f(x,y) é a imagem de entrada, r(x,y,u,v) é chamada de kernel de transformação
e a equação é calculada para u= 0,1,...,M-1 e v= 0,1,...,N-1. As variáveis u e v são
chamadas de variáveis de transformação. T(u,v) é chamada de transformada de
f(x,y). Dado T(u,v) podemos recuperar f(x,y) usando a transformada inversa
M 1 N 1
f ( x, y )   T (u, v) x( x, y, u, v)
(eq.2.6-31)
para x = 0,1,...,M-1 e y=0,1,...,N-1, onde s(x,y,u,v) é chamada de kernel de
transformação inversa.
u 0 v 0
© 1992–2008 R. C. Gonzalez & R. E. Woods
Digital Image Processing, 3rd ed.
Gonzalez & Woods
www.ImageProcessingPlace.com
Chapter 2
Digital Image Fundamentals
Abordagem geral para operações num domínio de
transformação linear.
© 1992–2008 R. C. Gonzalez & R. E. Woods
Digital Image Processing, 3rd ed.
Gonzalez & Woods
www.ImageProcessingPlace.com
Chapter 2
Digital Image Fundamentals
•
Um kernel de transformação é dito separável se
r ( x, y, u, v)  r1 ( x, u)r2 ( y, v)
•
Além disso, o kernel é dito simétrico se r1(x,y) é funcionalmente igual a r2(x,y) tal
que
r ( x, y, u, v)  r1 ( x, u)r1 ( y, v)
•
As mesmas definições e aplicam ao kernel de transformação inversa.
•
O kernel de Fourier usado para a transformada do exemplo da Fig. 2.40 é dado por:
r ( x, y, u, v)  e j 2 (ux / M vy / N )
e o kernel de Fourier da transformada inversa é dado por:
s ( x, y , u , v ) 
© 1992–2008 R. C. Gonzalez & R. E. Woods
1 j 2 (ux / M  vy / N )
e
MN
Digital Image Processing, 3rd ed.
Gonzalez & Woods
www.ImageProcessingPlace.com
Chapter 2
Digital Image Fundamentals
•
Substituindo os kernels do slide anterior nas equações de transformadas diretas e
inversas, temos o par de transformações de Fourier:
M 1 N 1
T (u, v)   f ( x, y)e  j 2 (ux / M vy / N )
Transformada (direta)
1 M 1 N 1
f ( x, y) 
T (u, v)e j 2 (ux / M vy / N )

MN u 0 v 0
Transformada inversa
x 0 y 0
•
A transformada de Fourier é separável e simétrica, e nesse caso, permitem que
transformadas 2D possam ser computadas usando transformadas 1D.
• Quando as transformadas direta e inversa satisfazem essas duas condições, e f(x,y) é
uma imagem quadrada de tamanho MxM, a equação geral da transformada pode ser
expressa como:
T = AFA
onde F é uma matriz MxM contendo os elementos de f(x,y), A é uma matriz MxM com
elementos aij=r1(i,j) e T é a transformada resultante MxM.
© 1992–2008 R. C. Gonzalez & R. E. Woods
Digital Image Processing, 3rd ed.
Gonzalez & Woods
www.ImageProcessingPlace.com
Chapter 2
Digital Image Fundamentals
•
Para obter a transformada inversa, multiplica-se pré- e posteriormente a equação
da transformada direta
T = AFA
pela matriz de transformação inversa:
BTB=BAFAB
• Se B= A-1,
F=BTB
indicando que F pode ser recuperada completamente da transformada direta.
• Se B não é igual a A-1, então usa-se uma aproximação:

F  BAFAB
•
Além da transformada de Fourier, um número de transformadas incluindo Walsh,
Hadamard, coseno, Haar, slant, podem ser expressos na equação geral (2.6-30,
2.6-31, ou, 2.6-38, 2.6-40).
© 1992–2008 R. C. Gonzalez & R. E. Woods
Digital Image Processing, 3rd ed.
Gonzalez & Woods
www.ImageProcessingPlace.com
Chapter 2
Digital Image Fundamentals
(a) Imagem corrompida
por interferência
senoidal.
(b) Magnitude da transformada de Fourier
mostrando a rajada de
energia responsável pel
interferência
(c) Máscara usada para
eliminar a interferência
(d) Resultado da
computação da inversa
da transformada de
Fourier
© 1992–2008 R. C. Gonzalez & R. E. Woods
Digital Image Processing, 3rd ed.
Gonzalez & Woods
www.ImageProcessingPlace.com
Chapter 2
Digital Image Fundamentals
•
•
•
Métodos probabilísticos
A probabilidade encontra a sua aplicação em processamento de imagens de várias
formas.
A forma mais simples é considerar os valores de intensidade como variáveis
aleatórias. Por exemplo, seja zi, i = 0,1,...,L-1 denotar os valores de todas as
possíveis intensidades numa imagem MxN. A probabilidade, p(zk) do nível de
intensidade zk ocorrer numa dada imagem é estimada como
nk
MN
one nk é o número de vezes que a intensidade zk ocorre na imagem e MN é
número total de pixels. Claramente
p( zk ) 
L 1
 p( z
k 0
© 1992–2008 R. C. Gonzalez & R. E. Woods
k
) 1
Digital Image Processing, 3rd ed.
Gonzalez & Woods
www.ImageProcessingPlace.com
Chapter 2
Digital Image Fundamentals
•
Dado p(zk) é possível determinar um número de importantes características. Por
exemplo, a intensidade média é dada por
L 1
m   zk p( zk )
•
k 0
A variância de intensidades é dada por
L 1
   ( z k  m) 2 p ( z k )
2
k 0
•
Normalmente o momento de ordem n de uma variável aleatória z em torno da
média é definido por
L 1
n ( z )   ( zk  m) n p( zk )
k 0
•
Sabe-se que
0 ( z)  1, 1 ( z)  0 e 2 ( z)   2
© 1992–2008 R. C. Gonzalez & R. E. Woods
Digital Image Processing, 3rd ed.
Gonzalez & Woods
www.ImageProcessingPlace.com
Chapter 2
Digital Image Fundamentals
Imagens mostrando:
(a) baixo contraste
(b) contraste médio
(c) alto contraste
© 1992–2008 R. C. Gonzalez & R. E. Woods
O desvio padrão nas intensidades
nas 3 imagens são 14.3, 31.6 e 49.2,
respectivamente. Os valores correspondentes de variância são 204.3,
997.8 e 2424.9. Ambos os conjuntos de
valores tem o mesmo significado, mas
como as intensidades variam no
intervalo [0,255] o desvio padrão faz
mais sentido intuitivo nesse caso.