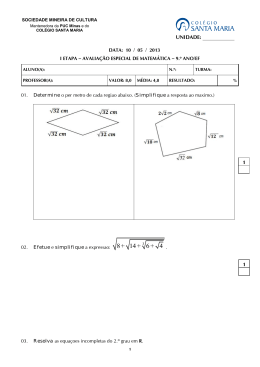
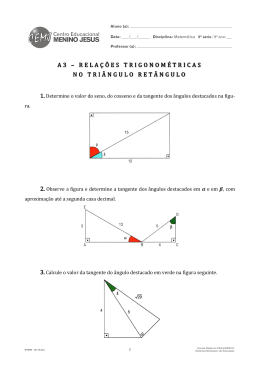
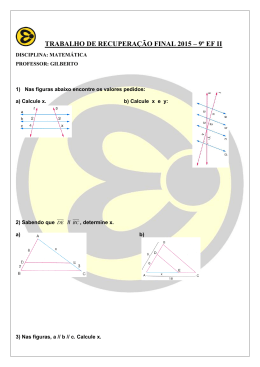
EXERCÍCIO – Inequações - 03
ALUNO(A):
PROFESSOR(A): Fabrício Dias
Nº:
TURMA:
%
1 MatPoint
Questão 01
Determine o conjunto verdade da inequação dada por
Questão 02
Determine os valores inteiros de k que satisfazem a inequação
2k − 3
>1 .
3−k
Questão 03
Por uma mensagem dos Estados Unidos para o Brasil, via fax, a Empresa de Correios e Telégrafos
(ECT) cobra R$1,37 pela primeira página e R$0,67 por página que se segue, completa ou não. Qual
o número mínimo de páginas de uma dessas mensagens para que seu preço ultrapasse o valor de
R$10,00?
Questão 04
Num concurso, a prova de Matemática apresentava 20 questões. Para cada questão respondida
corretamente, o candidato ganhava 3 pontos e, para cada questão respondida erradamente ou não
respondida, perdia 1 ponto. Sabendo-se que para ser aprovado deveria totalizar, nessa prova, um mínimo de
28 pontos, determine O MENOR NÚMERO de questões respondidas corretamente para que o candidato
fosse APROVADO.
Questão 05
Se -1 < 2x + 3 < 1, então 2 -x está entre:
a) 1 e 3
b) -1 e 0
c) 0 e 1
d) 1 e 2
e) 3 e 4
Questão 06
Fábio quer arrumar um emprego de modo que, do total do salário que receber, possa gastar 1/4 com
alimentação, 2/5 com aluguel e R$ 300,00 em roupas e lazer. Se, descontadas todas essas
despesas, ele ainda pretende que lhe sobrem no mínimo R$ 85,00, então, para que suas pretensões
sejam atendidas, seu salário deve ser no mínimo de quantos reais?
Questão 07
Três planos de telefonia celular são apresentados na tabela abaixo:
a) Qual é o plano mais vantajoso para alguém que utilize 25 minutos por mês?
b) A partir de quantos minutos de uso mensal o plano A é mais vantajoso que os outros dois?
Questão 08
Um estacionamento cobra R$ 6,00 pela primeira hora de uso, R$ 3,00 por hora adicional e tem uma
despesa diária de R$ 320,00. Considere-se um dia em que sejam cobradas, no total, 80 horas de
estacionamento. O número mínimo de usuários necessário para que o estacionamento obtenha
lucro nesse dia é:
a) 25
b) 26
c) 27
d) 28
e) 29
Questão 09
No triângulo retângulo representado abaixo cada um dos catetos mede 3cm.
Considere um ponto C da hipotenusa e o retângulo ABCD, sendo x a medida de AD .
Determine:
a) a área S do retângulo ABCD em função de x;
b) para que valor(es) de x se tem S > 1,25cm 2 .