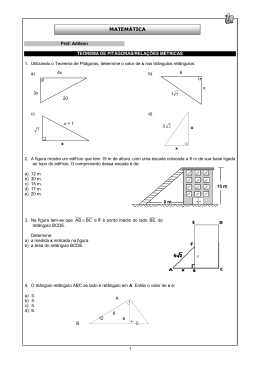
SOCIEDADE MINEIRA DE CULTURA
Mantenedora da PUC Minas e do
COLÉGIO SANTA MARIA
UNIDADE:
DATA: 10 / 05 / 2013
I ETAPA – AVALIAÇÃO ESPECIAL DE MATEMÁTICA – 9.º ANO/EF
ALUNO(A):
PROFESSOR(A):
01.
N.º:
VALOR: 8,0
MÉDIA: 4,8
TURMA:
RESULTADO:
%
Determine o perímetro de cada região abaixo. (Simplifique a resposta ao máximo.)
1
02.
Efetue e simplifique a expressão:
8 + 14 + 3 6 + 4
.
1
03.
Resolva as equações incompletas do 2.º grau em R.
1
a) x2 – 7 = 0
b)
3x
x2
–
=x
4
10
c)
x²  4
= x2 – 3
2
1
04.
Determine o valor da expressão
3
2
.

3 1
3 1
1
05.
A área da região plana do desenho é de 36 m2 e as medidas estão dadas em metros. Calcule o
valor de x.
Sugestão: Retire da área do retângulo de dimensões x+1 e x a área do retângulo de dimensões 3 e 2.
1
06.
Determine o valor da expressão
4

7
49  3  3 
1
+ 1-  : + 1+  .
64
3
 5 5 
2
1
07.
08.
Sabendo que a área do retângulo abaixo é igual a 32 cm2, a medida de seus lados é igual a
a)
8 cm e 2 cm.
b)
6 cm e 4 cm.
c)
6 cm e 2 cm.
d)
8 cm e 4 cm.
e)
8 cm e 6 cm.
1
O número n de atletas classificados para a disputa de certa prova final pode ser calculado por meio
da equação n2 – 2n – 3 = 0. Observando-se que n tem de ser um número natural, pode-se afirmar
que o maior número de atletas que se classificam para essa prova final é igual a
a)
2.
b)
3.
c)
4.
d)
5.
e)
6.
1
ECLO/gmf
3