1º) Dados os conjuntos A = {-2, -1, 0, 1, 3} e B = {0, 2, 3, 4, 6, 7, 10, 12, 24} e seja a relação de A⇾B,
R1 = {(x,y) ∈ AxB /
a)
b)
c)
d)
} determine:
O domínio, o Contra-domínio e a Imagem de cada relação.
Os pares ordenados da relação.
Represente a relações usando diagramas de flechas.
Diga se as relação é ou não função.
2º) Seja a função ( )
a)
2
b)
-2
c)
1
d)
-1
e)
0
, qual é o valor de
3º) Dada a função real, ( )
gráfico da função.
( )
( )?
, sabe-se que f(4) = -1, obtenha o valor de a e construa o
4º) Uma função afim é tal que: f(-2) = 4 e f(1) = 13 quanto é f(-3)
a) 1
b) 4
c) -3
d) -5
e) 2
5º) Um técnico de informática, que presta serviços em domicílios, cobra uma taxa fixa, que ela chama
de taxa de visitação, que independe do serviço a ser feito, e mais R$ 30,00 por hora de serviço ou
fração de hora (taxa de variação). Uma empresa o chamou para resolver uns problemas em algumas de
suas máquinas e ao final do serviço que durou 3 horas ele cobrou R$ 130,00. Sendo f(x) o preço a ser
pago ao técnico e x a quantidade de horas trabalhadas por ele, quantas horas ele trabalha em um
serviço que custa R$ R$ 220,00?
a) 4
b) 5
c) 6
d) 7
e) 8
6º) Dada a função afim f(x) = - 3x + 4, qual é o valor de 3f(1) + 2f(2)
a) – 2
b) 1
c) – 2
d) – 1
e) n.d.a.
7º) Dado o gráfico ao lado, responda:
a) Qual é a lei de formação da função?
b) faça o estudo dos sinais da função.
8º) Em cada caso abaixo, encontre a raiz da função, classifique-a em crescente, decrescente ou
constante e determine se ela é afim ou linear:
a) f(x) = - 10 + 2x
b) g(x) = 7x
c) h(x) = - 5x + 3
d) t(x) = - 9
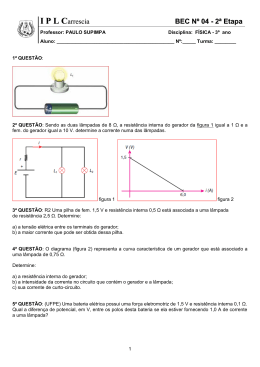
9º) Gerador é um tipo de aparelho que transforma um tipo de energia em energia elétrica. Se a potencia
(em watts) que um certo gerador lança num circuito elétrico é dada pela relação
, onde i
é a intensidade de corrente elétrica que atravessa o gerador, determine:
a)
A potência para i = 3 A, ou seja, ( )
b)
A potência para i = 1/5 A, ou seja, (
)
c)
Para qual valor de i,
d)
Quais o valores em que a função corta o eixo das abscissas (x)?
10º) Em um reservatório de água o nível Y varia com o tempo t, contando em horas a partir da meia
noite (0 h), conforme a função y = - 4,2 + 7,8t – 1,3t². O instante em que o reservatório está mais cheio
é:
11º) Numa empresa o custo C para produzir x unidades de um certo produto é dado por C = 3000 – 80x
+ x². Qual é o custo mínimo de produção dessa empresa?
12º) A função Real definida por f(x) = - x² + kx – 9 intercepta o eixo x em apenas um ponto, nestas
condições qual é o valor de k é:
13º) Um terreno retangular tem perímetro 28 cm. Sua área (A) pode ser obtida em função das medidas
dos seus lado e expressa por uma função quadrática:
a)
Qual é a expressão que determina a ares desse retângulo?
b)
Construa o gráfico da função encontrada.
14º) Gerador é um tipo de aparelho que transforma um tipo de energia em energia elétrica. Se a
potencia (em watts) que um certo gerador lança num circuito elétrico é dada pela relação
, onde i é a intensidade de corrente elétrica que atravessa o gerador, determine:
a) A potência para i = 3 A, ou seja, ( )
b) A potência para i = 1/5 A, ou seja, (
)
c) Para qual valor de i,
d) Quais o valores em que a função corta o eixo das abscissas (x)?
15º) Construa o gráfico da função ( )
16º) Qual é o conjunto solução da equação (
17º) A equação
a)
-1
b)
0
c)
1
d)
2
e)
3
18º) Dado o sistema {
.
)
√
?
tem duas raízes reais. O produto delas é:
, qual é o valor de x + y?
19º) Resolva a inequação ( )
.
20º) Numa certa cidade, o número de habitantes, num raio de r km a partir do seu centro, é dado por
( )
, em que k é uma constante e r > 0. Se há 98304 habitantes num raio de 5 km do centro,
quantos habitantes há num raio de 3 km do centro?
a)
32768
b)
4608
c)
3024
d)
2048
e)
1536
21º) Qual é o valor do
a) 1
b) 2
c) 3
d) 4
e) 5
√
?
22º) Qual é o valor do
a) -2
b) -1
c) 0
d) 1
e) 2
?
23º) Qual é o valor do
a) -1
b) -2
c) -3
d) 3
e) 2
24º) Qual é o valor do
a) 2
b) 3
c) 4
d) 1
e) 45
25º) Se o
a) 25
b) 4
c) 3
d) 15
e) 5
26º) dado o
a) 1
b) 2
c) 3
?
√
√
?
= 2, qual é o valor de b?
quanto vale o
d)1/2
e) 1/3
27º) Dados log 2 = 0,30, log 3 = 0,48 e log 5 = 0,7, qual é o valor de log 18?
a) 1,26
b) 0,32
c) 4,8
d) 2,34
e) 0,89
28º) Usando os dados da questão anterior e aplicando a mudança de base calcule o
a) 0,125
b) 0,625
c) 0,225
d) 0,200
e) 1,250
29º) Sabendo que
, podemos concluir que
a)
b)
c)
d)
e)
( )
30º) Para qual valor de x o
a) 60°
b) 45º
c) 30°
d) 90º
e) não é possível determinar.
?
é igual a:
.