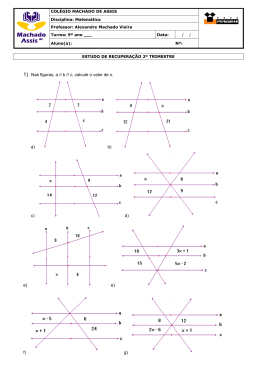
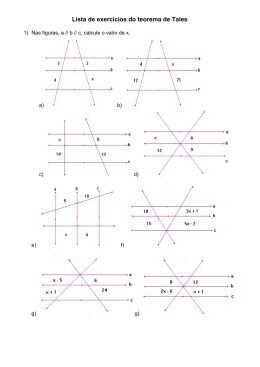
TEOREMA DE TALES
1. Na figura abaixo as retas r, s e t são
paralelas e cortadas pelas transversais m e
n.
(A) 30
(B) 6
(C) 200
(D) 80
(E) 20
4. Três retas paralelas são cortadas por duas
transversais, determine o valor de x.
Se AB = 2cm; BC = 6 cm e XY = 10 cm a
medida, em cm, de XZ é:
(A) 30
(B) 10
(C) 40
(D) 12
(E) 20
2. Na figura abaixo as retas r, s e t são
paralelas e cortadas pelas transversais m e
n.
Se AB = 30 cm; AC = 50 cm e XY = 6 cm a
medida, em cm, de XZ é:
(A) 30
(B) 10
(C) 40
(D) 12
(E) 20
(A) 6
(B) 10
(C) 15
(D) 8
(E) 2
5. Três retas paralelas são cortadas por duas
transversais, determine o valor de x.
(A) 15
(B) 2
(C) 6
(D) 27
(E) 4
6. Três retas paralelas são cortadas por duas
transversais, determine o valor de x.
3. Três retas paralelas são cortadas por duas
transversais, determine o valor de x.
(A) 3
(B) 2
(C) 6
(D) 27
(E) 4
1
7. Três retas paralelas são cortadas por duas
transversais, determine o valor de x.
(A) 8/7
(B) 2
(C) 6
(D) 27
(E) 4
8. Três retas paralelas são cortadas por duas
transversais, determine o valor de x.
(A) 3
(B) 2
(C) 6
(D) 27
(E) 4
9. Três retas paralelas são cortadas por duas
transversais, determine o valor de x.
(A) 3
(B) 2
(C) 6
(D) 27
(E) 4
11. Na figura abaixo as retas r, s e t são
paralelas e cortadas pelas transversais m e
n.
Se AB = a cm; BC = 10 cm; XY = b cm; YZ = 20
cm e a + b = 120 cm, então a medida, em cm, de
XZ é:
(A) 30
(B) 100
(C) 200
(D) 80
(E) 20
12. Na figura abaixo as retas r, s e t são
paralelas e cortadas pelas transversais m e
n.
(A) 3
(B) 2
(C) 6
(D) 27
(E) 4
10. Três retas paralelas são cortadas por duas
transversais, determine o valor de x.
Se AB = a cm; BC = 10 cm; XY = b cm; YZ = 20
cm e b – a = 40 cm, então a medida, em cm, de
XY é:
(A) 30
(B) 100
2
(C) 200
(D) 80
(E) 20
13. Três retas paralelas são cortadas por duas
transversais, determine o valor de x.
(A) 10
(B) 11
(C) 28
(D) 130/3
(E) 20
16. Três retas paralelas são cortadas por duas
transversais, determine o valor de x.
(A) 3
(B) 2
(C) 6
(D) 27
(E) 4
14. Na figura abaixo as retas r e s são
paralelas e cortadas pelas transversais m e
n.
Se AB = 40 cm; BC = 20 cm e AZ = 30 cm, então
a medida, em cm, de AB + AY é:
(A) 30
(B) 100
(C) 200
(D) 80
(E) 60
15. Três retas paralelas são cortadas por duas
transversais, determine o valor de x.
(A) 10
(B) 4,8
(C) 28
(D) 1,3
(E) 20
17. Na figura abaixo as retas r e s são
paralelas e cortadas pelas transversais m e
n.
Se AB = 40 cm; BC = 20 cm; CZ = 60 cm e AY
= 20 cm, então o perímetro do triângulo ACZ, em
cm, é:
(A) 30
(B) 100
(C) 150
(D) 80
(E) 60
18. Quatro retas paralelas são cortadas por
duas transversais, determine o valor de
x+y.
3
(A) 10
(B) 11
(C) 28
(D) 130/3
(E) 20
21. Na figura abaixo as retas r e s são
paralelas e cortadas pelas transversais m e
n.
(A) 10
(B) 11
(C) 28
(D) 130/3
(E) 20
19. Quatro retas paralelas são cortadas por
duas transversais, determine o valor de
x+y.
Se AB = a cm; BC = 20 cm; AY = b cm e YZ =
10 cm, com a + b = 60 cm - então a medida de
AY, em cm, é:
(A) 30
(B) 20
(C) 40
(D) 80
(E) 60
22. Na figura abaixo as retas r e s são
paralelas e cortadas pelas transversais m e
n.
(A) 10
(B) 11
(C) 28
(D) 130/3
(E) 20
20. Quatro retas paralelas são cortadas por
duas transversais, determine o valor de
x+y+z.
Se AB = 2 cm; BC = 1 cm e XY = 15 cm - então
a medida de BX, em cm, é:
(A) 10
(B) 20
(C) 30
(D) 5
(E) 2
23. Na figura abaixo as retas r e s são
paralelas e cortadas pelas transversais m e
n.
4
Se AB = 2x – 5 cm; BC = x2 cm; BY = 5 cm e
BX = 1 cm - então a medida de XY, em cm, é:
(A) 25
(B) 5
(C) 20
(D) 6
(E) 2
Se AB = 2 cm; BC = 10 cm e BY = 15 cm - então
a medida de XY, em cm, é:
26. O triângulo abaixo mostra duas retas
paralelas, determine o valor de x usando o
teorema de Tales.
(A) 10
(B) 18
(C) 20
(D) 5
(E) 2
24. Na figura abaixo as retas r e s são
paralelas e cortadas pelas transversais m e
n.
(A) 12
(B) 53
(C) 23
(D) 15
(E) 2
27. O triângulo abaixo mostra duas retas
paralelas, determine o valor de x usando o
teorema de Tales.
Se AB = 2 cm; AC = 12 cm e BY = 15 cm - então
a medida de XY, em cm, é:
(A) 10
(B) 18
(C) 20
(D) 5
(E) 2
25. Na figura abaixo as retas r e s são
paralelas e cortadas pelas transversais m e
n.
(A) 12
(B) 53
(C) 23
(D) 15
(E) 2
28. No triângulo abaixo EF e BC são
paralelas, determine o valor de x usando o
teorema de Tales.
5
(A) 12
(B) 3
(C) 23
(D) 5
(E) 2
31. Determine o valor numérico de x.
(A) 12
(B) 53
(C) 23
(D) 15
(E) 2
29. O triângulo abaixo mostra duas retas
paralelas, determine o valor de x usando o
teorema de Tales.
(A) 12
(B) 3
(C) 23
(D) 5
(E) 2
SEMELHANÇA ENTRE TRIÂNGULOS
32. Dados os triângulos retângulos ARE e
OTE:
(A) 12
(B) 53
(C) 23
(D) 15
(E) 2
30. O triângulo abaixo mostra duas retas
paralelas, determine o valor de x usando o
teorema de Tales.
Se AR = OE = AE/2 = 40 cm, então:
(A) TO = 10
(B) TO = 20
(C) TO = 30
(D) TO = 60
(E) TO = 15
33. Dado os triângulos retângulos ARE e
OTE:
6
Se OE = 20, TO = 5 e AE = 16, então:
(A) AR = 10
(B) AR = 12
(C) AR = 6
(D) AR = 4
(E) AR = 2
34. Um prédio tem sombra, pela luz solar,
projetada no solo horizontal com 70 m.
Simultaneamente um poste de 8m de
altura localizado nas proximidades deste
prédio tem sombra do mesmo tipo com 14
m. Calcule a altura do prédio.
A) 10 m
B) 20 m
C) 35 m
D) 40 m
E) 80 m
35. Um prédio tem sombra, pela luz solar,
projetada no solo horizontal com 70 m.
Simultaneamente um poste de 8m de
altura localizado nas proximidades deste
prédio também tem sua sombra projetada
no solo. Sabendo que neste instante os
raios solares fazem um ângulo de 45° com
o solo, calcule a altura do prédio e a
sombra do poste que, respectivamente,
são:
A) 70 m e 8 m
B) 35 m e 8 m
C) 70 m e 4 m
D) 35 m e 4 m
E) 20 m e 8 m
36. Considere a figura abaixo:
Se AB=18cm, AC = 12cm e DC = 6cm,
calcule o perímetro do quadrilátero
ABDE.
A) 10 cm
B) 20 cm
C) 35 cm
D) 40 cm
E) 80 cm
37. Dada a figura abaixo, determine o valor
de x.
(A) 10
(B) 20
(C) 30
(D) 45/4
(E) 29/4
7
38. Os polígonos são semelhantes se:
(A) Os lados são proporcionais e seus
ângulos correspondentes são
congruentes.
(B) Apenas os ângulos
correspondentes são congruentes.
(C) Apenas os lados correspondentes
são proporcionais.
(D) Os ângulos têm exatamente as
mesmas medidas.
(E) N.d.a.
39. Determine x e y nas figuras, sabendo que
a=b.
PONTOS NOTÁVEIS DE UM
TRIÂNGULO.
41. Das afirmações abaixo a única falsa é:
(A) Um triângulo eqüilátero tem todos
os lados iguais.
(B) O triângulo isóscele tem dois lados
iguais.
(C) O triângulo escaleno possui os três
lados diferentes.
(D) O teorema de Pitágoras relaciona
os lados de um triângulo
retângulo, supondo sempre que o
quadrado da hipotenusa é igual a
soma dos quadrados dos catetos.
(E) A soma dos ângulos internos de
qualquer triângulo é igual a 360°.
42. No triângulo abaixo NA é a bissetriz do
ângulo â, determine o valor do ângulo
externo x.
(A) 9; 32/3
(B) 9; 33/2
(C) 8; 32/2
(D) 2; 33/2
(E) N.d.a.
40. Determine DE=x, sabendo que o triangulo
ABC é retângulo em A e o triângulo DEC
é retângulo em D, AB=8cm, AC=15cm,
BC=17cm e CD=5cm.
(A) 8/3
(B) 1/6
(C) 4/7
(D) 2/3
(E) 1/8
(A) 60°
(B) 70°
(C) 90°
(D) 100°
(E) N.d.a.
43. (UCMG) Na figura, o ângulo ACD é reto.
O valor, em graus, do ângulo CBD é:
(A) 95
(B) 100
(C) 105
(D) 120
(E) 130
44. (PUC)
8
Se na figura temos: medidas D=20°, AC e
BC congruentes, CD e BD congruentes,
entao a medida do ângulo A é:
(A) 100°
(B) 80°
(C) 70°
(D) 40°
(E) 20°
45. Ortocentro é o ponto onde se interceptam
as 3alturas de um triângulo, isto é, as
perpendiculares traçadas desde os
vértices até aos lados opostos. Essa
definição está representada na figura:
46. A mediatriz é a reta perpendicular a um
lado do triângulo, traçada pelo seu ponto
médio. As três mediatrizes de um
triângulo se encontram em um único
ponto, o circuncentro, que é o centro da
circunferência circunscrita ao triângulo,
que passa pelos três vértices do triângulo.
O diâmetro dessa circunferência pode ser
achado pela lei dos senos. Essa definição
está representada na figura:
(A)
(B)
(A)
(B)
(C)
(D)
(E) N.d.a.
(C)
(D)
(E) N.d.a.
47. Mediana é o segmento de reta que une
cada vértice do triângulo ao ponto médio
do lado oposto. A mediana relativa à
hipotenusa em um triângulo retângulo
mede metade da hipotenusa. O ponto de
interseção das três medianas é o
baricentro ou centro de gravidade do
triângulo.
9
(A)
(B)
(B)
(C)
(C)
(D)
(E) N.d.a.
(D)
(E) N.d.a.
48. A bissetriz interna de um triângulo
corresponde ao segmento de reta que parte
de um vértice, e vai até o lado oposto do
vértice em que partiu, dividindo o seu
ângulo em dois ângulos congruentes. Em
um triângulo há três bissetrizes internas,
sendo que o ponto de interseção delas
chama-se incentro.
REVISÃO DE POTÊNCIA.
49. O valor numérico de 3 6 é:
(A)243
(B) 81
(C)729
(D)27
(E)n.d.a.
50. O valor numérico de 2 3 é:
(A)0,125
(B)0,333...
(D)8
(E)0,25
(C)0,75
51. A potência que melhor representa 72 é:
(A) 2.5²
(B) 2 3.3²
(C) 2 3.3³
(D) 2 3.3
(E)n.d.a.
52. A única representação correta de
(B) 2 4
(E) 2 3
(A)2³
2 4
(C) 2 5
53. A representação de 1024 é:
 
(D) 2 3
(B)  2
8
(A) 2 8
2
1
é:
16
(D)
 
(C) 2 2
5
(E)N.d.a.
(A)
54. O valor numérico de
3 4 .3 2
é:
36
10
(A) 1
(E)6
(B)2
(C) 3
(D) 4
64. Resolvendo a expressão
0
55. O valor de 9 é:
(A) 2
(E)9
(B) 1
(C) 3
(D) 0
56. A representação correta de
(A) 5
5
2
5
2
3
(B) 5
(E) 5
3
2
3

0
,
256.4 9
, obtemos:
87
(B) 64
(C)128
(E)512
65. Simplificando
5 2 é:
(C) 5

41 / 2  2 1  (3) 0  0,1 . 25 3
obtemos:
(A) 1/2
(B)7/2
(C) 3/2
(D)1/4
(E)2/5
1
2
1
2
(D)
(A)32
(D)256
4
5
9 3.27 4.3 7
:
3 1.243 2
(B) 3
(C) 9
66. Resolva
57. A representação de 8 é:
(A) 2
8
3
2
3
2
(B) 2
4
2
(C) 2
(A) 1
(E)n.d.a.
2
3
(D)
(D)27
125 6.25 3
:
5 6.25 7
(B) 125
(C) 225
(E)340
67. Simplifique
(E)n.d.a
(A)1
625
58. O valor da expressão numérica
7 4.[7 3  7 6 ] é:
(A) 1
(B) 1/7
(C)1/49
(D)7
(E)49
68. Calcule
59. O valor numérico da expressão
8 5  2 6  4 3 é:
(A) 1/2
(B) 1/4
(C) 1/8
(D)1/16
(E)1/32
(A)1
(D)1/27
 
38. 3 2
2
(D)
3
 1  18
  .3
3
(B) 1/3
(E)1/81
:
(C) 1/9
RADICAIS
6
4 2
, obtemos:
4  2 12
(B) 2 6
(C) 2 7
(E) 2 9
60. Resolvendo
(A) 2 5
(D) 2 8
12
8
5
0
61. A representação correta de (0,1)³ é:
(A)1/100
(B) 1/1000
(C)1/10000
(D) 1000
(E)n.d.a.
69. Extraindo o máximo do radical
4
16 ,
3
 27 ,
obtemos:
(A) 1.
(B) 2.
(C) 3
(D) 4
(E) N.d.a.
5
1
62. A forma decimal que representa   é:
 10 
(A) 0,001
(B)0,0001
(C) 0,00001
(D)0,000001
(E)0,00000001
 1  5
63. O resultado de  
 2 
(A) 1/4
(B) 1/32
(D)1/8
(E)n.d.a.
 2
.8 é:

(C)1/16
1
: 
2
4
70. Extraindo o máximo do radical
obtemos:
(A) -1
(B) -2.
(C) 3
(D) -3
(E) N.d.a.
11
71. Extraindo o máximo do radical
6
64 ,
obtemos:
(A) 1.
(B) 2.
(C) 3
(D) 4
(E) N.d.a.
77. A representação de
72. Extraindo o máximo do radical - 3 64 ,
obtemos:
(A) -3.
(B) -2.
(C) -4
(D) 4
(E) N.d.a.
73. Extraindo o máximo do radical
3
1
125 ,
obtemos:
(A) 1/2.
(B) 1/5
(C) 1/25
(D) 5
(E) N.d.a.
(B) 2
5
6
1
6
(C) 2
(D) 2 3
(E) N.d.a.
76. A representação de 6 4 é:
(A) 2 0,333...
(B) 2 0,111...
(A)
(B)
3
3
3
81
6
9
3
obtemos:
(A) 2
81 .
(D) 27
(E) N.d.a.
Simplifique as expressões abaixo:
80. 4 2  3 2  2  4 2  2 =
81. 31 3  42 3  2 3  4 3  4 3 
74. Extraindo o máximo do radical
6
5
8
(A) 30,333...
(B) 30,111...
(C) 30, 25
(D) 31,33...
(E) N.d.a.
78. Resolva a expressão 16 0, 25  810, 25  250,5 :
(A) 6
(B) 7
(C) 8
(D) 9
(E) 10
79. 33 3 pode ser representado por:
(C)
(A) 1/2.
(B) 1/5
(C) 1/25
(D) 5
(E) N.d.a.
75. A representação correta de
(C) 2 0, 25
(D) 21,33...
(E) N.d.a.
6
32
6
1
64 ,
82.  5  53 5  3 5  5 5  35 5 
5
3
83.
3 5 3 
3
3
2
84. 5 3  2 2  3 3  2 2  32 3 
85. 3 5  53 5  6 3  3 3  6 
2
3
86. 3 10  2 10 
10 
10 
3
2
1
1
87. 2 7 
5
5  7 7 7 
2
2
88. 6 8  32  2 50 
89. 108  27  2 75  2 3 
90. 2 24  3 54  2 50  5 6 
91. 18a 2  50a²  98a²  2a² 
36 x³ y  9 x³ y  100 x³ y  4 x³ y 
1
1
93.
48 
75 
2
5
94. 4 3  7 18  5 48  200 
92.
95. 18  98  50  72  2 
12
96.
360  490  250  1000  810 
97. 2 27  48  3 3  12  3 
98. 3 18  32 3  100 48  3 200 
8
2


3
3
Calcule os seguintes produtos.
100. 3 a  3 a² 
129.
10  10 
130.
5 5 
131.
6 6 
99. 9
2 5 
101.
102.
3
103.
104.
3
105.
5
106.
107.
108.
109.
110.
111.
112.
113.
114.
115.
116.
117.
118.
3 5 
5  23 
3  3 5  3 10 
133.
134.
3
16  5 6 
6 8 
40  5 
xy  y 
ac  acw 


2  2  7
2 3  3  2
a   a  ab  
5 x  2 x  3 y  
 3  2   3  2  
 5  2   5  2  
 6  5   6  5  
 10  2   10  2  
10  1  10 
2 3 
119.
132.
120.
5  20 
121.
40  5 
122.
6 8 
135.
136.
137.
138.
 3  2  3  2  
 5  3  5  3  
 4  3  4  3  
 10  6  10  6  
 6  2  6  2  
 5  2  5  2  
 6  5  6  5  
Efetue as divisões:
139.
32  8 
140.
32  2 
141.
3
21  3 3 
142.
3
108  3 2 
72  6 
143.
Racionalize as frações abaixo:
2
144.
3
1
145.
123.
124.
8 6 
125.
6 3 
5
146.
2
2
126.
127.
128.
5
3
8
53 2 

10
2
3
16  5 6 
150.

6
148.
149.

5
147.
1
1


40
5

3
5
3
2



42  2 
13