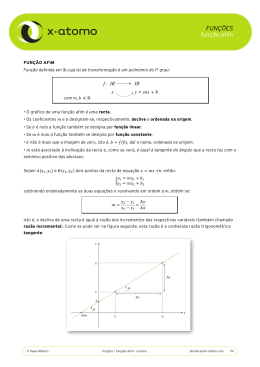
Função Afim
Definição:
Uma função f: IR → IR (f de IR em IR) chama-se
função afim quando existem dois números reais a e
b tal que f(x) = ax + b, para todo x є IR.
Exemplos:
1) f(x) = 2x + 1 (a = 2, b = 1)
2) f(x) = -x + 4 (a = -1, b = 4)
1
1
3) f(x) = x + 5 (a = , b = 5)
3
3
4) f(x) = 4x (a = 4, b = 0)
Valor de uma função afim
Na função afim f(x) = 5x + 1, podemos determinar:
f(1) = 5 • 1 +1 = 5 + 1 = 6. Logo, f(1) = 6.
f(-3)=5(-3) + 1 = -15 + 1 = -14. Logo, f(-3) = -14.
Casos particulares importantes da função afim
1ª) Função linear
f: IR
→ IR definida por f(x) = ax para todo x є IR. Nesse caso, b = 0.
Exemplos:
• f(x) = -2x
(a= -2, b = 0)
1
1
• f(x) = x (a = , b = 0)
5
5
• f(x) = 3 x (a = 3 , b = 0)
2ª) Função constante
f: IR
→ IR definida por f(x) = b para todo x є IR. Nesse caso, a = 0.
Exemplos:
• f(x) = 3
• f(x) = -2
• f(x) = 2
3
• f(x) =
4
3ª) Função identidade
f: IR
→ IR definida por f(x) = x para todo x є IR. Nesse caso, a = 1 e b = 0.
•
f(x) = x
1
4ª) Translação
f: IR
→ IR definida por f(x) = x + b para todo x є IR. Nesse caso, a = 1 e b ≠ 0.
Exemplos:
• f(x) = x + 2
• f(x) = x - 3
1
• f(x) = x +
2
3
• f(x) = x 5
Determinação de uma função afim conhecendo-se seus valores em dois
pontos distintos
Uma função f(x) = ax + b fica inteiramente determinada quando conhecemos dois
valores f(x1) e f(x2) para quaisquer x1 e x2 reais, com x1 ≠ x2 . Ou seja, com esses dados
determinamos os valores de a e de b.
Por exemplo, escreva a função afim f(x) = ax + b, sabendo que:
f(1) = 5 e f(-3) = -7
• se f(1) = 5 , então para x = 1 tem-se:
f(x) = ax + b
f(1) = 5
x=1
a=?
b=?
f(1) = a · 1 + b
5=a+b
Ou seja, a + b = 5.
•
se f(-3) = -7 , então para x = -3 tem-se:
f(x) = ax + b
f(-3) = -7
x = -3
a=?
b=?
f(-3) = a · (-3) + b
-7 = -3a + b
Ou seja, -3a + b = -7.
Determinamos os valores de a e b resolvendo os sistema de equações:
a+b=5
-3a + b = -7
- a – b = - 5 (multiplica-se a equação por -1.)
-3a + b = -7
-4a = -12
− 12
a=3
−4
Como a + b = 5 e a = 3, então:
a+b=5
3+b=5
b=5–3
b=2
Logo a função afim f(x) = ax + b tal que f(1) = 5 e f(-3) = -7 é dada por f(x) = 3x + 2.
a=
2
Traçado de gráficos de funções afins
Construindo gráficos de algumas funções afins no plano cartesiano.
3
Função Identidade (a = 1 e b = 0)
Translação (a = 1 e b ≠ 0)
4
Função constante (a = 0)
Função afim crescente e decrescente
1º Caso: a > 0.
Vamos construir, o gráfico da função f(x) = 2x -1.
5
2º Caso: a < 0.
Vamos construir, o gráfico da função f(x) = -3x -1.
6
Exercícios Propostos
1) Classifique as funções abaixo em afim, linear, identidade, constante e translação:
a. f(x) = 5x + 2
1
h. f(x) = x
b. f(x) = -x + 3
7
c. f(x) = 7
x
1
i. f(x) = +
d. f(x) = x
2
3
e. f(x) = 3x
j. f(x) = 2 – 3x
f. f(x) = x + 5
g. f(x) = -3
2) Dada a função f(x) = -2x + 3, determine:
a. f(1)
b. f(0)
1
c. f  
3
5
3) Dada a função afim f(x) = 1 - x, calcule.
2
a. f(0)
b. f(-1)
 1
d. f  − 
 2
4) Determine o que se pede.
a. Sabendo que f(x+1) = 2x, calcule f(4).
1
b. Dada a função f(5x -1) = x - , calcule f(0).
5
5) Sendo f(x) = 3x – 4 e g(x) = 2x + 1, determine os valores reais de x para que se
tenha f(x) < g(x).
6) Dada a função afim f(x) = 2x + 3, determine os valores reais de x para que:
a. f(x) = 1
1
c. f(x) =
b. f(x) = 0
3
d. f(x) = 0,75
7) Na produção de peças, uma indústria tem um custo fixo de R$ 8,00 mais um custo
variável de R$ 0,50 por unidade produzida. Sendo x o número de unidades
produzidas:
a. Escreva a lei da função que fornece o custo total de x peças;
b. Calcule o custo de 100 peças;
c. Escreva a taxa de crescimento da função.
8) Uma pessoa tinha no banco um saldo positivo de R$ 560,00. Após um saque no
caixa eletrônico que fornece apenas notas de R$ 50,00, expresse a lei da função que
fornece o novo saldo, que é dado em função do número x de notas retiradas.
9) Determine o valor da função afim f(x) = -3x + 4 para:
a. x = 1
d. x = 1,5
e. x = k +1
1
b. x =
f. x = a + b
3
c. x = 0
7
10) Escreva a função afim f(x) = ax + b, sabendo que:
a. f(-1) = 7 e f(2) = 1
b. f(2) = -2 e f(1) = 1
11)
1
Dada a função f(x) = ax + b e sabendo que f(3) = 5 e f(-2) = -5, calcule f   .
2
12)
Dada a função f(x) = ax + 2, determine o valor de a para que se tenha f(4) = 22.
13) Construa, num sistema ortogonal, o gráfico das seguintes funções, dizendo em cada
caso se a função é crescente ou decrescente:
a. f(x) = x + 2
b. f(x) = - x + 2
c. f(x) = 1 + 2x
14) Faça o gráfico das funções f(x) = x, g(x) = x + 1 e h(x) = x – 2.
15) Construa o gráfico das funções:
a. f(x) = x e g(x) = -x
16) Escreva a função f(x) = ax + b cujo gráfico, num sistema cartesiano ortogonal, é
dado por:
a.
8